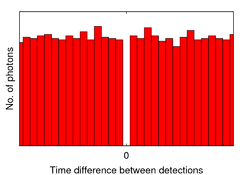
Photon antibunching

Under photon antibunching refers to the non-occurrence of temporal correlations of individual photons from the same source. Antibunching is a purely quantum mechanical effect and does not occur with classic light sources such as thermal light sources . The non-classic character of a light source can be proven by measuring anti-bunching.

The effect was demonstrated in 1977 by Leonard Mandel and his collaborators, H. Jeff Kimble , M. Dagenais.

It is z. B. for a single photon source emitted light from a single atom. This creates gaps in time because the atom must first be excited again before another photon can be emitted. The time correlation for is therefore less than 1. ${\displaystyle \gamma (\tau )}$ ${\displaystyle \tau \to 0}$

Some authors define antibunching as a sub-Poisson statistic, which means that the variance is smaller than for a Poisson distribution . Although this usually occurs at the same time , it is a different phenomenon. ${\displaystyle \gamma (0)<1}$

Clear explanation

A single atom with only two states represents a perfect single photon source. The emission of a photon occurs when the atom changes from the excited to the ground state. Before another photon can be emitted, the atom must first return to the excited state (e.g. by illuminating it with resonant laser light). So there is always a finite time difference between the emission of two photons of the same atom, so two photons can never be emitted at the same time ( antibunching ; Bunch is the English-language term for particle packet).

Classic light sources, on the other hand, consist of macroscopic emitters that contain a large number of atoms. These emit photons independently of one another, so that no antibunching can be observed there, on the contrary, the photons increasingly strike a detector at the same time ( photon bunching ).

Quantitative description

For a Fock state with photons, the second order correlation function applies: ${\displaystyle |n\rangle }$ ${\displaystyle n}$

${\displaystyle \gamma ^{(2)}(0)=1-{\frac {1}{n}}.}$

So perfect antibunching ( ) only occurs for the jib state . ${\displaystyle \gamma ^{(2)}(0)=0}$ ${\displaystyle |1\rangle }$

Evaluation of the correlation function

Typical experimental signature for antibunching a single photon source.

The second order correlation function is measured:

${\displaystyle \gamma (\tau )={\frac {\langle I_{1}(t)I_{2}(t+\tau )\rangle }{\langle I_{1}(t)\rangle \langle I_{2}(t)\rangle }}}$,

d. i. the specification of the expected value after a period of time after the arrival of a photon to detect another. In the case of the single photon emitter considered so far, the intensity can be expressed using the creation and annihilation operators , which are related to the transition operators of the two-level system, because: ${\displaystyle \tau }$

${\displaystyle {\hat {I}}_{i}={\hat {E}}_{i}^{-}\cdot {\hat {E}}_{i}^{+}}$ and

${\displaystyle {\hat {E}}_{i}^{-}\propto {\hat {a}}^{\dagger }}$,

so we

${\displaystyle \gamma (\tau )={\frac {\langle I_{1}(t)I_{2}(t+\tau )\rangle }{\langle I_{1}(t)\rangle \langle I_{2}(t)\rangle }}={\frac {\langle {\hat {E}}_{1}^{-}(t){\hat {E}}_{2}^{-}(t+\tau ){\hat {E}}_{1}^{+}(t){\hat {E}}_{2}^{+}(t+\tau )\rangle }{\langle {\hat {E}}_{1}^{-}(t){\hat {E}}_{1}^{+}(t)\rangle \langle {\hat {E}}_{2}^{-}(t){\hat {E}}_{2}^{+}(t)\rangle }}={\frac {\langle {\hat {a}}^{\dagger }(t){\hat {a}}^{\dagger }(t+\tau ){\hat {a}}(t){\hat {a}}(t+\tau )\rangle }{\langle {\hat {a}}^{\dagger }(t){\hat {a}}(t)\rangle \langle {\hat {a}}^{\dagger }(t){\hat {a}}(t)\rangle }}}$

receive. For the case of the jib _{n = 1} state we get specifically:

${\displaystyle \gamma (\tau )={\frac {\langle {\hat {a}}^{\dagger }(t){\hat {a}}^{\dagger }(t+\tau ){\hat {a}}(t){\hat {a}}(t+\tau )\rangle }{\langle {\hat {a}}^{\dagger }(t){\hat {a}}(t)\rangle \langle {\hat {a}}^{\dagger }(t){\hat {a}}(t)\rangle }}{\xrightarrow {\tau \rightarrow 0}}{\frac {\langle {\hat {a}}^{\dagger }{\hat {a}}^{\dagger }{\hat {a}}{\hat {a}}\rangle }{\langle {\hat {a}}^{\dagger }{\hat {a}}\rangle ^{2}}}={\frac {\langle n(n-1)\rangle }{\langle n\rangle ^{2}}}}$,

using the properties of the creation and annihilation operators. Insertion gives:

${\displaystyle \gamma (0)\vert _{n=1}=0}$.

In general, the following applies to non-classical states: At the time of the measurement of a first photon ( ), fewer photons are detected than before or after. This is how these conditions can be identified: ${\displaystyle \tau =0}$

${\displaystyle \,\gamma (0)<\gamma (\tau )}$with ; ${\displaystyle \left|\tau \right|>0}$

this of course includes the special case . ${\displaystyle \gamma (0)=0}$

Individual evidence

1. ^ HJ Kimble, M. Dagenais, L. Mandel: Photon Antibunching in Resonance Fluorescence . In: Physical Review Letters . tape 39 , no. 11 , September 12, 1977, pp. 691-695 , doi : 10.1103 / PhysRevLett.39.691 . Predicted in HJ Kimble, L. Mandel: Theory of resonance fluorescence . In: Physical Review A . tape
    13 , no. 6 , June 1, 1976, p. 2123-2144 , doi : 10.1103 / PhysRevA.13.2123 . Independently of this predicted in HJ Carmichael, DF Walls : A quantum-mechanical master equation treatment of the dynamical Stark effect . In: Journal of Physics B: Atomic and Molecular Physics . tape
    9 , no. June 8 , 1976, p. 1199-1219 , doi : 10.1088 / 0022-3700 / 9/8/007 .
2. ^ Mark Fox: Quantum Optics: An Introduction . Oxford University Press, 2006, ISBN 978-0-19-856673-1 ( limited preview in Google Book Search).
3. ↑ XT Zou, L. Mandel: Photon-antibunching and sub-Poissonian photon statistics . In: Phys. Rev. A . tape 41 , 1990, pp. 475 , doi : 10.1103 / PhysRevA.41.475 .
4. ↑ R.Vyas, S. Singh: antibunching and photoemission waiting times . In: J. Opt. Soc. At the. B . 17, No. 4, 2000, pp. 634-637. doi : 10.1364 / JOSAB.17.000634 .

literature

• Harry Paul: Photons: An Introduction to Quantum Optics . Vieweg + Teubner Verlag, 1999, ISBN 978-3-519-13222-6 .
• Pierre Meystre, Murray Sargent III: Elements of Quantum Optics . Springer, 2007, ISBN 978-3-540-74209-8 .

Web links

• Photon antibunching on the Becker & Hickl tutorial page