Line theory
The line theory is a branch of electrical engineering . It deals with phenomena on electrical lines, the length of which is in the order of magnitude of the wavelength of the transmitted signal spectrum or more, and is mainly used in telecommunications , high-frequency technology , pulse technology and in the electrical power supply for high-voltage lines .
The line theory uses the model of the electric double line and describes this by the equivalent circuit diagram of an "infinitely short" line section, the elements of which are determined by the line coverings. Without determining the electromagnetic field herself with the help of Maxwell's equations , she derives a system of partial differential equations (the so-called line equations ) from it and tries to solve these with various mathematical methods adapted to the respective boundary conditions .
This makes it possible to qualitatively understand the processes and wave phenomena (e.g. reflections , standing waves , negative overshoot , resistance transformations ) that occur in connection with cables, to grasp them quantitatively and to interpret them correctly for practical applications. Finally, rules are created for the use of cables as a component in electrical engineering, especially in communications engineering and electronics .
background
Only for direct current or alternating current of low frequency can a line be roughly described with the ohmic resistance of the line cross-sectional area, conductivity and length. As soon as the wavelength of the signals is in the order of magnitude of the line length or fast switching processes on lines are to be described, this greatly simplified model is not sufficient. Due to the capacitance and inductance layers on each line, the signals propagate at the maximum speed of light . If the spatial expansion of an electrical system is so large that the transit time of the signals to be processed can no longer be neglected, special wave phenomena occur in addition to the "normal" behavior. The description of such systems requires mathematical methods that include the location of the signals in the considerations.
For example, an alternating voltage of 1 GHz in a vacuum has a wavelength of about 30 cm. Wave processes therefore play a major role on the circuit boards of modern computers . Due to the high-frequency clocking , the data is represented and transmitted by very short pulses with steep edges. Therefore, such systems would not be realizable without applying the knowledge of the line theory.
For the methods of classical line theory, however, the technical conductor spacing must not be greater than half the wavelength of the resulting waves and the resistance layer must not be too large, so that only the transverse electromagnetic fields (TEM waves) play a role. Only then can an “infinitely short” line section be described by an equivalent circuit diagram made up of concentrated components. If this is not the case, Maxwell's equations must be solved directly. This is what high and maximum frequency technology deals with in the theories of cavity waves and antenna systems .
history
The laying of transatlantic submarine cables , which began in 1850, and the severe distortions that occur with such long cables, required a theoretical analysis of the processes on "long lines". William Thomson was the first to deal with the description of the processes on lines around 1855 . In 1886, Oliver Heaviside formulated this knowledge in its current form as a line equation and thus founded the general line theory . He found the Heaviside condition named after him , from which it could be seen that the problems of distortion were essentially caused by the high line capacitance. Rudolf Franke looked at the line for the first time in 1891 using the four-pole theory . To solve the distortion problem, Mihajlo Pupin proposed in 1900 the winding of cables to artificially increase their inductance. This meant that nothing stood in the way of the implementation of long telephone lines . By 1903, George Ashley Campbell viewed the line as a chain leader . With the advent of high-frequency technology at the beginning of the 20th century, it was necessary to treat even short lines with the means of line theory. They could be regarded as lossless and, in addition to signal transmission, they could also be used as components (e.g. for resistance transformation). Up until then, all of these applications were based on sinusoidal signals and could therefore be solved with the help of the complex AC calculation. In the middle of the 20th century, impulse technology and later digital technology required the unadulterated transmission of short impulses over cables. For this it was necessary to carry out the analysis with the help of an operator calculation, graphically with a pulse schedule or (if memory-free components with non-linear characteristics are connected) with the Bergeron method . Numerical methods were developed to analyze the pulse propagation on lossy lines.
The line equations
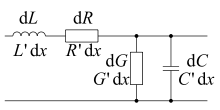
The line equations of a homogeneous linear two-wire line can be determined from the equivalent circuit diagram of such a line section of infinitesimal length d x shown in the following figure :
The quantities contained therein are the line coverages multiplied by the length d x : the inductance cover L ′ , the capacitance cover C ′ , the resistance cover R ′ and the discharge cover G ′ .
From voltage u (x, t) and current i (x, t) at the beginning, from voltage u (x + dx, t) and current i (x + dx, t) at the end of this element of the line result with the aid of Mesh set and junction set the two partial differential equations of the homogeneous line (the detailed derivation takes place in the article line equation ):
Voltage u and current i are introduced downwards or to the right (in the + x direction). The main task of line theory is the solution of this DGL system for the initial and boundary conditions of the most diverse practical technical applications and thus the determination of the course of voltage u (x, t) and current i (x, t) on the line as a function of Place x and time t .
Special case: Sinusoidal signals
In many cases of alternating current technology and classic communications technology, it is practically sufficient to consider the voltage and the current both as purely sinusoidal (harmonic) and as complete switch-on and transient processes. Then only (stationary) sinusoidal signals occur on a line. In this special case, the complex alternating current calculation can be used and because there is no time dependency, the line equations are reduced to a system of ordinary differential equations for the complex amplitudes U (x) and I (x) that exist on the line and are dependent on location x :
They are often referred to in the literature as "complex line equations". In this case, a closed solution of the line equations can be given if the two line ends are wired linearly.
Special case: lossless lines
In the case of short and / or high-frequency lines , the losses due to resistance and dissipation deposits can practically be neglected. This simplifies the line equations as follows:
If you transform this DGL system into a single partial differential equation, you get the classic one-dimensional wave equation .
Because neither attenuation nor distortion then occurs on the line (the Heaviside condition is fulfilled “automatically”), the equations can in many cases be solved easily and the solutions obtained can be interpreted particularly clearly. The results of this idealization nevertheless correctly represent the essential behavior of a line and are also of didactic importance for the "introduction to line theory".
Special case: Sinusoidal signals on the lossless line
By combining these two special cases, the following particularly simple form of the "complex line equations" is obtained:
Since their main importance lies in high-frequency technology , they are the starting point for the theory of high-frequency lines , the “didactic prime example” of line theory.
The general solution of the line equations
The first step in line theory to solve the line equations is to determine the general solution of the DGL system. This has freely selectable (integration) constants or functions, which then have to be defined by defining the initial and boundary conditions adapted to the specific application . Since the DGL system of the line equations is linear, the general solution can in the general case be determined with the help of the Laplace transform, for example.
When determining the general solution, one encounters essential parameters of the line, such as the phase and group velocity or the propagation constant (propagation constant ) and the wave resistance (wave impedance). In general, the last two quantities are complicated operators in the sense of operator calculation . In particular, the propagation constant is responsible for the propagation of the waves on the line, their speed, their damping and their deformation.
In the following special cases, however, the general solution is relatively easy to determine.
Special case: lossless lines
With the definitions for the (real) wave resistance of the lossless line
and the (constant) phase velocity of the lossless line
one obtains the general (so-called d'Alembert's ) solution
Here u h (t) and u r (t) are two time functions that still have to be defined by the boundary conditions. Proof of correctness can be provided by inserting it into the “lossless” line equations.
This general solution can be interpreted as follows:
- The left term of the solution represents a wave (arbitrarily shaped) running from the beginning to the end of the line.
- The right term represents a wave returning from the end to the beginning of the line.
- Both waves have the speed v 0 .
- They are neither attenuated nor distorted in their form on the line.
- The wave resistance Z 0 represents the ratio of voltage and current of the respective wave.
Special case: Sinusoidal signals
With the definitions for the complex wave resistance (wave impedance)
and the complex propagation constant (propagation constant )
one obtains the general solution for linear differential equations according to the solution method (e.g. exponential approach )
U h0 and U r0 are the two as yet undefined complex integration constants which have to be determined by the boundary conditions. Proof of correctness can be provided by inserting it into the “complex line equations”.
This general solution can be interpreted as follows:
- The left term of the solution represents a sinusoidal wave ( traveling wave ) running from the beginning to the end of the line .
- The right term represents a sinusoidal wave returning from the end to the beginning of the line.
- These waves are damped due to the (generally frequency-dependent) damping constant α and rotated in phase according to the (always) frequency-dependent phase constant β. Because of the generally non-linear frequency dependence of the phase constant, a distinction must be made between phase velocity and group velocity .
- The complex wave impedance Z Ltg represents the ratio of the complex amplitudes of voltage and current of the respective wave. In contrast, the ratio of total voltage U (x) to total current I (x) is not constant due to the interference of waves traveling back and forth, es standing waves arise , which are characterized by their standing wave ratio .
Special case: Distortion-free line
Oliver Heaviside has already shown that on a line whose line coverings the Heaviside condition named after him
meet the "waves running over the line" in their form (despite attenuation) are not distorted. At the same time, this means that the phase velocity does not depend on the frequency and therefore no dispersion occurs, that is, neighboring frequency groups do not “diverge”. However, this desirable property is normally not fulfilled by a real line due to the predominant capacity occupancy. In order to achieve the longest possible distortion-free telephone lines, the inductance coating has been artificially increased ( coiled line , Krarup cable ).
The operational behavior of a line
In the second step, line theory determines a concrete (particular) solution from the general solution by eliminating the remaining degrees of freedom by defining boundary and initial conditions.
- If, on the one hand, a line is used for signal transmission, then an active (generator) two-pole connection is connected at its beginning and a passive load two-pole connection at its end. If a wave traveling over the line hits the end or the beginning of the line, then it can be reflected there. It is generally changed in its size and in its shape (if it is not sinusoidal). The impedance of the respective termination and the wave resistance determine how this happens. The reflection factors at the beginning and at the end of the line are used to quantitatively describe the reflections .
- On the other hand it is possible to lead a four pole to look at and from the general solution quadripole parameters to be determined.
Under the following special boundary conditions, line theory has developed methods to determine closed particulate solutions:
- If both the generator and the load two-pole of a lossless line contain only linear ohmic resistances, then there is a closed solution as an infinite series (due to multiple reflections) . The propagation of a single pulse edge can be graphically displayed and calculated as a pulse schedule ( lattice diagram ).
- If the generator and / or load two-pole of a lossless line contain non-linear, memory-free resistors, then the propagation of a single pulse edge can be determined graphically using the Bergeron method .
- If both the generator and the load dipole contain any linear components, then the solution must be determined using the Laplace transformation (or another operator calculation). If the line is lossless , this can be done manually , if, on the other hand, it is lossy , then computational / numerical methods are generally necessary.
- If both the generator and the load dipole of a lossy line contain any linear components and the generator voltage is (purely) sinusoidal, then the solution can be determined using the complex alternating current calculation.
Special case: infinitely long line
In this case there is only one going wave (the left term of the general solution). The ratio of voltage to current at each point on the line corresponds to the characteristic impedance. An important "interpretation" of the wave resistance follows from this: The input resistance of an infinitely long line is equal to its wave resistance. The two-pole generator acts like a voltage divider from its internal resistance and the wave resistance.
This theoretical case is approximately reached in practice when the line is very long and its attenuation is so great that the wave reflected at the end is practically "no longer measurable" at the beginning of the line.
Special case: line terminated with the wave impedance on the output side
If a finitely long line is terminated with a passive two-pole connection, the impedance of which is equal to the wave resistance of the line, then it has the same effect as if the line were to continue indefinitely. Therefore, a line terminated ( adapted ) with the characteristic impedance behaves exactly like an infinitely long line, in particular there is only one incoming wave and its input resistance is also equal to the characteristic impedance.
Special case: line terminated with the wave impedance on the input side
In this case, a wave runs from the input to the output, is partially reflected there (and generally deformed) and runs back to the input, where its energy is “consumed” in the generator's internal resistance.
Example: Sinusoidal signals on the lossless line
For the "prime example" of the line theory, the practically important high-frequency line , the complete solutions should be given here. The general solution in this case is simplified too
where the propagation constant is only represented by the phase constant, which is linearly dependent on the frequency, due to the lack of attenuation:
Here, λ is the wavelength on the line, which is smaller by the shortening factor than the wavelength of an electromagnetic wave of the same frequency in a vacuum.
Operating behavior of a line terminated at both ends
If, on a line of length L, the generator bipole has an internal (complex) impedance Z G and an open circuit voltage U G and the load bipole has an internal (complex) impedance Z 2 , the general solution after determining the two constants U h0 and U r0 is the final solution as the superposition of an incoming and a returning wave
During the derivation of this solution, the complex reflection factor at the output are defined as
and the complex reflection factor at the input as
This means that the signals on the line can be determined at each point x for each specific linear connection of the output and input. It turns out that the ratio of the outgoing and return waves depends solely on the wiring at the output and that it is advantageous to define the generalized (complex) reflection factor for any point x on the line as follows:
In practice, the easily measurable course of the amplitude or the effective value of the mostly existing standing waves is often of interest. It arises relative to the incoming wave at the exit
If one relates the maximum and minimum values of the standing wave, one obtains the standing wave ratio (SWR) as an important measure for the mismatch :
The high-frequency line as a four-pole
If you specify alternatively voltage U 2 and current I 2 at the end of the line as boundary conditions for determining a particulate solution , then you get for the voltage U (x) and the current I (x) on the line:
For x = 0, one calculates the voltage U 1 and the current I 1 at the beginning of the line and thus obtains the four-pole chain equations for the line:
They are the basis for using a line section as a high-frequency component.
Line transformation
The line transformation or impedance transformation describes the property of being able to change the impedance at the beginning of a line, designated as Z 1 , through the length L Ltg and the line impedance Z Ltg and through the termination of the line with the impedance Z 2 . An approximately lossless line is assumed for which the relationship applies:
with the wave number and the wavelength in the relationship:
The line impedance Z Ltg is also referred to in this context as the characteristic impedance of the line - it is independent of the termination and length of the line and is determined by the line coverings. Furthermore, the wavelength in this context along a transmission line is different from the wavelength when an electromagnetic wave propagates in free space. This relationship is described by the shortening factor.
Starting from this relationship, which is fundamental for the line transformation, line theory analyzes the transformation behavior of the line for certain line lengths such as the important special cases of a λ / 4 line or λ / 2 line and for certain line terminations such as matching , short circuit , open circuit, real termination, reactance as Degree and general complex degree.

Alternatively, line transformations can also be carried out with the aid of the Smith diagram : To do this, the standardized terminating resistor in the Smith diagram is simply rotated at an angle
around the point (line length , generator frequency , relative permittivity , vacuum speed of light ). The normalized input impedance can then be read directly from the Smith diagram.
Short-circuited line
For a line short-circuited at the end ( Z 2 = 0), the equation is simplified to
The ratio L Ltg / λ = m determines, based on the sign rules of the tangent function , whether this U-shaped line behaves like a capacitance, an inductance or an oscillating circuit:
- For 1/4> m> 0 it is an inductance
- For 1/4 = m it is a parallel resonant circuit with the resonance wavelengths λ; λ / 3; λ / 5; ...
- For 1/2> m> 1/4 it is a capacity.
- For 1/2 = m it is a series resonant circuit with the resonance wavelengths λ; λ / 2; λ / 4; ...
This behavior continues periodically for odd multiples.
Note : L Ltg is the actual geometric pipe length. The influence of the shortening factor is contained in the wavelength .
In some special radio devices for very high frequencies, a movable short-circuit clip is used for stub lines or Lecher lines in order to be able to set the desired property. As a rule, no symmetrical double wire is used, which radiates energy and therefore only has a low quality factor , but a closed, cylinder-symmetrical cup circle .
Open line
For a line open at the end ( Z 2 → ∞) the equation is simplified to
The ratio L Ltg / λ = m determines whether the idling line behaves like a capacitance, an inductance or a resonant circuit:
- For 1/4> m> 0 it is a capacitance
- For 1/4 = m it is a series resonant circuit with the resonance wavelengths λ; λ / 2; λ / 4; ...
- For 1/2> m> 1/4 it is an inductance.
- For 1/2 = m it is a parallel resonant circuit with the resonance wavelengths λ; λ / 3; λ / 5; ...
This behavior continues periodically for odd multiples.
λ / 4 line
For the line length λ / 4, the equation for the transformation relationship with the impedance at the beginning of a line is simplified to:
If the λ / 4-long line is short-circuited at the end ( Z 2 → 0), it acts like an open circuit at the input, i.e. it is high-resistance with Z 1 → ∞. Conversely, a λ / 4-long line open at the end acts like a short circuit at the input. The line impedance Z Ltg does not matter in either case.
The λ / 4 transformation continues periodically for odd multiples.
Application examples
In the picture above, a method is shown how a high-frequency double line can be supported and grounded, even though it is isolated at the nominal wavelength λ. The inner conductor of an air-filled coaxial line for high transmission powers can be supported in a comparable way by a λ / 4 cup circle.
If you remove the lower cross bracket, the λ / 4-long stub acts like a selective short circuit for very specific frequencies, while it isolates with direct current. This can prevent the unwanted spread of HF energy with a defined frequency.
Some components of radar technology such as branch duplexers and ring couplers are based on the impedance transformation of λ / 4 lines.
The electrical energy is coupled into a waveguide with a probe (rod antenna) which protrudes λ / 4 from the closed end into the waveguide. The electromagnetic wave detached from the probe of the coupler "sees" the infinitely high resistance of the short-circuited λ / 4 line on three sides, so it can only propagate in the remaining direction.
With microwave ovens , the resonance seal (i.e. the door seal that prevents the escape of microwave energy) is a circumferential band made of a λ / 4 channel that is exactly 3 cm wide and the metal surfaces of which do not touch. This width matches the wavelength of 12 cm generated by the magnetron. This makes it possible to “lock in” the electromagnetic radiation field in the interior without using fault-prone contacts.
The Wilkinson divider can be explained most simply as a power adder: Two transmitters or antennas, each with the source impedance Z 0, deliver signals to the ports P2 and P3 in phase. The respective following λ / 4 lines with the impedance transform to 2 · Z 0 at port P1, which again results in the total impedance Z 0 through parallel connection . The resistance 2 · Z 0 on the right between P2 and P3 has no effect as long as the signals arriving there are in phase. It converts the energy of signals out of phase into heat.
λ / 2 line
A λ / 2-long line does not transform the output impedance and the following applies to the impedance at the input regardless of the line impedance of the λ / 2-line:
If a λ / 2-long line is short-circuited at the end ( Z 2 = 0), it also acts like a short-circuit at the input. Conversely, a λ / 2-long line that is open at the end also acts like an open circuit at the input.
Application examples
In radio technology, dipole antennas are often used , the task of which is to transform the impedance of the transmitter output to the characteristic impedance of the vacuum (377 Ω) so that the energy can be radiated efficiently.
Fed to a non- interrupted λ / 2 dipole at one end, there is measured an impedance Z 1 ≈ 2200 Ω. Because this value deviates too much from the wave impedance of a coaxial cable (Z ≈ 50 Ω), a direct connection would lead to an intolerable mismatch. In the method just described - strictly speaking - two λ / 4 bars were operated electrically in parallel, therefore each of the two has the impedance Z 1 ≈ 4400 Ω.
In order to lower the dipole impedance, the dipole is usually separated in the middle, because this is where the significantly lower value Z ≈ 70 Ω, which is better suited to the cable impedance, is measured. This measurement result can also be interpreted as a series connection of two 35 Ω resistors - each λ / 4 rod has the impedance Z a = 35 Ω. Such ground-plane antennas are used in medium-wave radio transmitters, this impedance Z at the lower end actually 2 is measured = 35 Ω, when the upper end remains free.
If you insert these measured values 4400 Ω and 35 Ω on both sides of a λ / 4 rod into the transformation equation for the λ / 4 line:
one obtains Z Ltg = 392 Ω, which is close to the value of the free space wave resistance Z 0 .
Further areas of line theory
In order to solve some practically important problems, the classic line theory based on the homogeneous double line with constant line coverings is supplemented by the following sub-areas:
- Influence of the skin effect on the line coverings and the wave propagation
- Refraction due to faults on the line or at coupling points of lines
- Equivalent circuits for short lines
- Line circuits and use of the line as a component
- Wave propagation on multi-conductor systems
- Coupled lines and directional couplers
- Crosstalk between different lines
Lines in complex structures
The solution of the line equations in four-pole parameter form (e.g. as S, Z or Y parameters) can be mirrored in numerical or formula-based numerical or symbolic CAD systems for advanced considerations as a matrix, which in turn are linear assemblies with n Mesh gate matrices. On the basis of Kirchhoff's laws, the more than 30 output quantities of high-frequency electronics known from standard CAD systems such as voltage and current amplification, input and output impedance, generalized scatter parameters, various profit concepts, etc., result either as numbers or as fully automatically derived formula expressions. In practice, all formulas will be derived automatically from many lines and other linear assemblies (R, L, C, transformers, linearized transistors, etc.), especially with more complicated structures.
Transfer of conduction theory to acoustic waves and heat waves
It is particularly pleasant that the entire electrical line theory with the complete terminology of CAD systems can be transferred to many other questions with very simple substitutions, e.g. B. on plane acoustic waves and plane heat waves, so that such problems can be analyzed excellently with the CAD systems of high frequency electronics. The optimization algorithms and all the conveniences of the systems are thus available. Since the differential equations are the same except for substitutions, no new problem arises.
Flat acoustic waves, which propagate in the x-direction with pressure p x = U and particle speed v x = I, are described in line theory because of the analog differential equations for lossless material by R '= 0, G' = 0, L '= ρ (consistency) and C 'as modulus of elasticity or compressibility (in the case of gases depending on the adiabatic coefficient). The calculation z. B. the speed of sound v = 1 / (L'C ') 1/2 would drop as a trivial secondary result. A task that is still very easy to solve would be the question of the frequency-dependent sound insulation of a triple-glazed window pane. It would be calculated using the chain connection of 5 four-pole lines made of glass-air-glass-air-glass, with the acoustic wave resistance (L '/ C') 1/2 of air being taken as the generator and load impedance . The calculation of the problem does not differ in any way from the circuit calculations in high-frequency electronics. The vague term “insulation” then becomes more precise to the standard term “profit”, which is well known from electronics, G = | s 21G | 2 with s 21G as a generalized scattering parameter, as it is implemented in every CAD system. If f = 1 kHz z. B. G = 1.5E-3, one would have 28.2 dB attenuation (insulation).
Flat heat waves can also be easily analyzed with the tools of conduction theory. Here U corresponds to the temperature and I to the heat flow through an area A. G '= 0 and L' = 0 applies. The quantities R 'and C' are determined from thermal conductivity, specific heat and material density. A heat conduction is a strongly damping conduction with α = β. Since mostly αL ≫1, there is no returning wave and the input impedance of the line is equal to the characteristic impedance (R '/ jωC') 1/2 . Temperature and heat flow (voltage and current) are then phase-shifted by 45 ° at x = 0.
Other applications of conduction theory
In general, for all problems whose differential equations can be formally traced back to the structure of the above line equations, the problem is completely solved after establishing the analogy quantities for U, I and R ', L', G 'and C'.
In addition to plane heat waves and acoustic waves, this class of physical problems also includes plane electromagnetic waves that strike a loss-free layer sequence with different values for permeability, permittivity and thickness L at an angle. The solution of Maxwell's equations of a section can then be rewritten for the components of the electric and magnetic field in a quadrupole form with wave resistance and spread, each of which depends on the material values, layer thicknesses and angles. The generalized scattering parameters s 11G and s 21G then give, as is usual in high-frequency electronics , with | s 21G | 2 the transmitted and with | s 11G | 2 indicates the reflected power fraction.
The most ideal amplifier is always a traveling wave amplifier, in which a wave flies into a line without reflection, is amplified with negative α, migrates without dispersion and at the end is transmitted without reflection into the load. In the IC design, they are implemented in the microwave range approximately as a line consisting of a few ladder sections each consisting of Ls and Cs, whereby instead of G 'an FET is used, which with its current source ensures α <0 and thus amplifies the incoming wave. In the case of optical fibers , the analogue is an erbium-doped fiber amplifier. In the medical field, blood vessels can be modeled with conduction equations.
Limits of Leadership Theory
The line theory is no longer applicable at the latest when the waves begin to spread in a zigzag, but also when more complex structures have to be analyzed. If z. If, for example, two 75 ohm lines are connected to each other, one of which is a TV coaxial cable and the other a microscopic microstrip line, the connector transition is reflection-free according to line theory, but in reality it is by no means. This is where the line theory ends and Maxwell's equations have to be solved (see Electronics # High Frequency Electronics ).
literature
- Heinrich Schröder: Electrical Communication Engineering, Volume I . Publishing house for Radio-Foto-Kinotechnik GmbH, Berlin-Borsigwalde 1966.
- Peter Vielhauer : Theory of transmission on electrical lines . Verlag Technik, Berlin 1970.
- Hans-Georg Unger : Electromagnetic waves on lines . Dr. Alfred Hüthig Verlag, Heidelberg 1980, ISBN 3-7785-0601-3 .
- Claus-Christian Timmermann : High-frequency electronics with CAD, volume 1. Lines, four-pole, transistor models and simulation with numerical and symbolic CAD / CAE systems . PROFUND Verlag, Plankstadt 2003, ISBN 3-932651-21-9 .
- Gerhard Wunsch : History of Systems Theory . Akademie-Verlag, Leipzig 1985.
Web links
- Literature on line theory in the catalog of the German National Library
- Script for the lecture "Electronics" by Prof. Dr. Klaus Wille, Technical University of Dortmund ( Memento from January 24, 2014 in the Internet Archive ) (PDF; 1.5 MB)