Smith Chart

The title of this article is ambiguous. For the Smith diagram known in materials science, see fatigue strength # Smith diagram .

The Smith chart ( English Smith chart ) is an aid to the complex AC calculation, with the calculations of complex resistances ( impedances ) can be traced back to a geometric construction. It was first introduced by Phillip Smith in 1939 .

High resolution blank Smith Chart

The Smith chart is also used in line theory for impedance matching . The Smith chart used there differs from the one shown here only in the way the axes are interpreted or the axis labeling.

construction

Conformal mapping of the impedance plane (z-plane) into the reflection factor plane (r-plane), which forms the Smith diagram within the unit circle

The diagram is circular and has a complex coordinate system. It is based on conformal mapping

${\displaystyle r(z)={\frac {z-1}{z+1}}}$

the complex impedance level to the likewise complex reflection factor level which results from the definition of the reflection factor. ${\displaystyle r}$

In this figure, the right half-impedance plane is mapped onto the inside of the unit circle in the reflection factor plane. The inside of the unit circle in the reflection factor plane corresponds exactly to the area of ​​the Smith diagram. The left half of the impedance level, which corresponds to the area outside of the Smith diagram in the reflection factor level, is irrelevant because it corresponds to impedances with a negative real value, which do not occur in passive components.

In mathematics, this transformation of one level into another is also known as the Möbius transformation . It obeys the general form

${\displaystyle f(z)={\frac {az+b}{cz+d}}}$

The image has the special property that the image of a number z in the impedance plane, for example

${\displaystyle z=2+\mathrm {j} }$

and their reciprocal value :

${\displaystyle 1/z=1/(2+\mathrm {j} )=0{,}4-0{,}2\mathrm {j} }$

are point-symmetrical about the origin in the reflection factor plane. In electrical engineering , the symbol is used for the imaginary unit . The Smith diagram can thus be used as both an impedance and an admittance diagram. ${\displaystyle \mathrm {j} }$

When calculating a parallel connection , the reciprocal value of the total impedance results as the sum of the reciprocal values ​​of the partial impedances. This reciprocal value formation is replaced geometrically in the Smith diagram by a reflection at the center. Normalized values ​​are always used in the Smith diagram. This has the advantage that one is independent of variables such as the actual frequency, wavelength or impedance.

In line theory, e.g. B. in impedance matching problems, the reflection factor Γ and standing wave ratio (SWR) can easily be determined from the Smith diagram without complex calculation. To do this, the length of the connecting line between the origin and the intersection of the two circles of the normalized impedance is measured. The phase of the reflection factor can be read off the extension of the line on the outer scale of the Smith chart. The SWR can be determined indirectly via the reflection factor, but can also be read directly from the Smith diagram - as the intersection of the real axis to the right of the circle center with the circle, which is given by the amount of the reflection factor.

If you want to calculate the reflection factor Γ at any point on a line, this corresponds to a rotation of the reflection factor by the normalized line length at the end of the line on the reflection factor circle either towards the generator, i.e. clockwise, or towards the load, i.e. counterclockwise .

The following figure shows the basic relationships in two Smith diagrams using the example of line theory. It can be seen that the Smith diagram shows inductive impedance values ​​in the upper half and capacitive impedance values ​​in the lower half.

On a line with the impedance Z ₀ with a line termination Z _L , the impedance z normalized to the line impedance is shown in the left partial image . z = 0 represents the case of a short circuit, when idling, z is infinite, this corresponds to the point on the far right. The real parts of the normalized impedance are shown in blue circles, the imaginary parts on them are normal curves in green. The reflection factor Γ is shown in the right part of the picture.

Working with the Smith Chart

• Normalization: All elements are normalized, i.e. h., impedances are by their characteristic impedance divided, admittances with multiplied and then entered in the Smith chart. ${\displaystyle Z_{0}}$ ${\displaystyle Z_{0}}$
• Impedances connected in series can be added directly.
• Impedances connected in parallel must first be brought to admittance form; i.e. to be mirrored around the center point. Alternatively, two Smith charts can be used one above the other, with one Smith chart rotated by 180 °. This means that reflections around the center point can be implemented as a transition from one diagram to the other.
• Branch line : The branch line is to be converted into an equivalent impedance and, depending on the arrangement, added like a serial or parallel impedance.
• Movement on the line: Impedance diagram or admittance diagram, rotate the appropriate line length to the generator (clockwise) or to the load (counterclockwise).
• SWR: The SWR is obtained by rotating the point at the location you are looking for clockwise around the center on the real axis and reading the corresponding value.
• Short circuit: the point on the far left in the diagram.
• Idle: the point on the far right in the diagram.

Smith diagrams on paper for graphic determination are primarily used in the field of training and teaching and for documentation. In practical use, Smith charts usually appear in the context of appropriate programs. Even complex measuring devices such as network analyzers can usually display measured data directly in the form of Smith diagrams.

The original advantage and the intention to simplify the complex calculations in the form of graphical determination of the numerical values ​​has disappeared due to the wide availability of high-performance pocket calculators and computers with corresponding software packages. The graphic representation of impedance curves in technical documents and data sheets has remained the primary application.

example

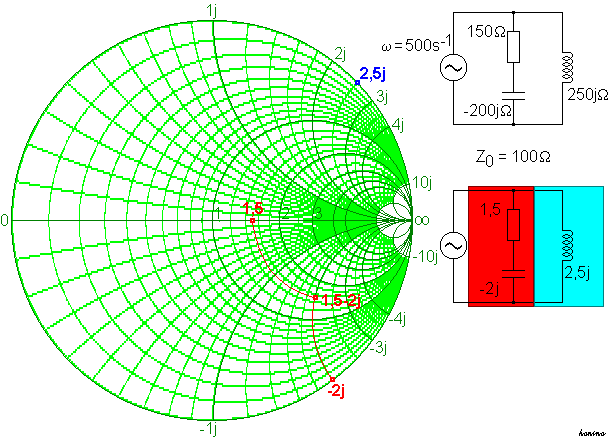
An ohmic resistor R = 150 Ω and a capacitor C = 10 μF are connected in series, with a coil L = 0.5 H in parallel . The circuit is connected to a generator whose frequency is f = 79.6 Hz.

The angular frequency is then ω = 2π f  = 500 s ⁻¹ .

For the complex resistance (the impedance ) of the capacitor follows

${\displaystyle X_{\mathrm {C} }={\frac {1}{\mathrm {j} \omega C}}=-\mathrm {j} {\frac {1}{\omega C}}=-200\mathrm {j} \ \Omega }$,

for the impedance of the coil one calculates

${\displaystyle X_{\mathrm {L} }=\mathrm {j} \omega L=250\mathrm {j} \ \Omega }$.

When connecting a resistor and a capacitor in series, the values ​​are simply added together and produced

${\displaystyle X_{1}=150\ \Omega -200\mathrm {j} \ \Omega }$.

In order to be able to enter the values ​​in the Smith chart, in which large numbers can no longer be displayed, normalize with a suitable reference resistor, e.g. B. Z ₀ = 100 Ω by dividing all values ​​by it. Then it will be

${\displaystyle X_{1}=1{,}5-2\mathrm {j} }$ (Resistor and capacitor)

and

${\displaystyle X_{2}=2{,}5\mathrm {j} }$ (Kitchen sink).

These two impedances are connected in parallel . So for the total impedance X is

${\displaystyle {\frac {1}{X}}={\frac {1}{X_{1}}}+{\frac {1}{X_{2}}}}$.

These reciprocal values ​​are obtained in the Smith diagram by mirroring at the center of the circle.

They amount to

${\displaystyle {\frac {1}{X_{1}}}=0{,}24+0{,}32\mathrm {j} \quad {\text{und}}\quad {\frac {1}{X_{2}}}=-0{,}4\mathrm {j} }$ .

The addition of the two reciprocal values ​​is done arithmetically or in the Smith diagram by "counting" on the coordinate grid.

You get

${\displaystyle {\frac {1}{X}}=0{,}24-0{,}08\mathrm {j} }$

In order to determine the total impedance X , the reciprocal value has to be calculated. So the point just obtained is reflected at the center of the circle.

As a result one finds

${\displaystyle X=3{,}75+1{,}25\mathrm {j} }$.

Since you previously divided by 100 Ω, you now have to multiply with it again. The final impedance of the entire circuit is thus

${\displaystyle X=375\,\mathrm {\Omega } +125\mathrm {j} \,\mathrm {\Omega } }$.

It can therefore alternatively be represented by a series connection of a resistance of 375 Ω and a coil of 125j Ω (at ω = 500 s ^{−1, this} corresponds to an inductance of 0.25 H).

3D Smith Chart

Illustration of a 3D Smith Chart

There are also generalized three-dimensional Smith diagrams that project active and passive networks together onto the Riemannian sphere .

literature

• Chris Bowik, John Blyer, Cheryl Ajluni: RF Circuit Design . 2nd Edition. Newnes, 2008, ISBN 978-0-7506-8518-4 .
• Joachim Müller: Smith diagram, introduction and practical guide . beam-Verlag, Marburg 2009, ISBN 978-3-88976-155-2 .
• PH Smith: Electronic applications of the Smith chart . McGraw-Hill, 1969, ISBN 978-0-07-058930-8 .

Web links

Commons : Smith charts  - collection of images, videos and audio files

• Smith Chart tool for impedance matching (runs in the browser)
• Smith chart (PDF; 53 kB)
• Smith chart with adjustable parameters as PDF (A4 and US letter)
• Brief instructions for the Smith chart (PDF; 199 kB)
• Java program for displaying Smith diagrams, open source, runs on Linux, MacOS and Windows

Individual evidence

1. ↑ PH Smith: Transmission Line Calculator , Electronics, Vol. 12, No. 1, pp 29-31, January 1939
2. ↑ PH Smith: An Improved Transmission Line Calculator , Electronics, Vol. 17, No. 1, pp 130-133, 318-325, January 1944
3. ^ Andrei Muller, Pablo Soto, D. Dascalu, D. Neculoiu, VE Boria A 3D Smith chart based on the Riemann sphere for Active and Passive Microwave Circuits , Microwave and Wireless Components Letters Online