Fatigue strength
The fatigue strength (engl. Fatigue behavior ) is a term used in materials science , and refers to the deformation and failure behavior of materials under cyclic stress. It is examined in the Wöhler experiment , from the results of which the Wöhler curve can be constructed. The Wöhler curve indicates the number of load changes that can be tolerated up to the expected fatigue fracture, depending on the deflection stress . In addition, the Wöhler curve can be divided into the areas of short-term strength, fatigue strength or fatigue strength. Diagrams such as the Haigh diagram or the Smith diagram can be used to show the fatigue strength. Fatigue strength or fatigue strength as well as fatigue strength have a major influence on the dimensioning of components in engineering .
Differentiation of the vibrating from the static load
The loading of a component or a material sample can be static or dynamic. In the case of static loading, material parameters such as the yield point or tensile strength can be determined in a tensile test . Static load here means the load on a body (object) with a constant force from a constant direction. As an example, placing a stone on a table is mentioned here. The stone has a constant mass and exerts a constant force on the table due to the acceleration of gravity . If the force exceeds a certain value, the table will collapse.
In the case of dynamic stress, however, the component is subjected to load changes, and the permissible stress in a material drops: A break can occur even if the tensile strength has not yet been reached and often without leaving the linear-elastic range of the stress-strain diagram . A screw that z. B. is used to attach an exhaust to the vehicle, can break due to the vibrating load of the vehicle movement, although the actual yield point was not reached. This effect can be intensified by corrosion and / or temperature changes. Such problems arose for the first time with the advent of the railroad. According to static calculations, the wheels of the wagons should have easily absorbed the stresses while driving without being damaged in the process. However, more and more railroad cars failed because the axles were broken. August Wöhler investigated this phenomenon from 1858 and discovered that oscillating loads can damage a component even if it is obviously not damaged by a single load with the same force.
The dynamic loads are usually understood as vibrations . A wheel set shaft of a railway wagon experiences, for example, a periodically oscillating load when rolling, since each revolution represents a load change. But also non-periodic loads, such as switching on and off, can be viewed as oscillating stress.
Wöhler line and differentiation between short-term, long-term and fatigue strength
For the construction and dimensioning of a component that is subject to an oscillating load, it must be known how many load changes it can survive before it breaks. This property is examined in the Wöhler test , which is standardized according to DIN 50100. For this purpose, the test bodies are cyclically loaded with high-frequency pulsators, mostly with a sinusoidal stress-time function. Depending on how the experiment is carried out, the stress can arise from tensile / compressive loads, bending , torsion or shear forces. Load amplitudes and the stress ratio between underload and overload (the so-called degree of rest ) are constant. The test runs until a defined failure (breakage, crack) occurs or a specified number of limit cycles is reached. Test specimens that reach the limit number of cycles without recognizable failure are referred to as runners.
The maximum number of load changes for a certain load amplitude can be read from the Wöhler diagram. It depends on the material properties (cyclically hardening / cyclically softening), the force or the resulting tension and the type of load (increasing pressure load, increasing tensile load or changing load). With the same displacement amplitude, the changing load damages the component the most.
In the Wöhler diagram, the nominal stress amplitude is usually plotted linearly or logarithmically over the logarithmically represented, tolerable number of cycles . The resulting curve is called a Wöhler curve . Because the range of fatigue strength is a straight line in a double logarithmic representation, the term Wöhler line has also established itself. If you look at a Wöhler curve (right), you will notice three different areas of the graph, which are referred to as short-term strength K, long-term strength Z and fatigue strength D.
- K is the range of short-term strength or short-term fatigue strength ( low cycle fatigue , LCF) below approx. 10 4 to 10 5 cycles. This type of fatigue occurs at high plastic strain amplitudes, which lead to early failure. The Coffin-Manson plot is usually used to represent this area more precisely . In the case of a load that leads to breakage within a quarter of the backlash, one speaks of the static strength, which is also determined in the tensile test . The area of short-term strength is only of minor importance for technical applications.
- Z is the area of the fatigue strength and fatigue life also fatigue strength (engl. High cycle fatigue , HCF) between 10 4 and depending on the material approximately 2 x 10 6 oscillating games, in which the Wohler curve at double logarithmic representation almost straight runs. The straight line can be described by the Basquin equation .
- D is the subsequent area of the so-called fatigue strength or fatigue strength ( very high cycle fatigue , VHCF). In ferritic-pearlitic steels, the fatigue strength range begins at around 1–5 · 10 6 load changes. It is controversial but today, if there is a real endurance limit at all or whether it (Engl. At very high numbers of cycles ultra high cycle fatigue , UHCF) also comes at very low loads to failure. In austenitic steels and base materials with a face-centered cubic crystal lattice (e.g. aluminum , gold , copper ), the tolerable amplitude continues to decrease. There is no “real” fatigue strength here. Therefore, the tolerable amplitude with 10 8 load changes is usually referred to as fatigue strength. If a component is subject to constant corrosion or greatly increased temperatures, fatigue strength can no longer be expected.
In the literature, the VHCF is often presented as the HCF area. There is then no separation into three areas, but only into the LCF area and the HCF area (depending on the literature, from 10 4 to 10 6 vibration cycles).
Occasionally, the probability that a component will break is also of interest. For this purpose, the Wöhler diagram is expanded to a three-dimensional coordinate system. The values of deflection stress , number of load cycles and probability of breakage are plotted on the axes; the mathematical description is based on a scatter band function (SBF). This SBF has six constants, which are determined from the flat Wöhler diagram and the scatter of the fatigue strengths. The most important result from the SAQ is the so-called zero break line , the probability of which is set individually with the help of the confidence intervals (e.g. 1 ppm, 10 ppm). With this evaluation of the single-stage Wöhler test it is also possible to make statistically reliable statements about the development of the breakage probability under multi-stage operating load. Influences of the medium voltage are taken into account in the statement on the probability of breakage, influences of the environment such as temperature fluctuations or corrosion usually have to be considered separately.
Fatigue strength
Below a certain maximum load and without the occurrence of time-dependent damage mechanisms (e.g. corrosion), some materials can (theoretically) withstand an infinite number of vibrations (load changes). Components that are subject to real operational use show this behavior only in exceptional cases and under certain conditions. In most cases, the component is not designed to be fatigue-resistant, but to be operationally stable. In addition, materials with a face-centered cubic crystal lattice, including many non-ferrous metals such as aluminum , do not show a limit cycle number . Here, even with low load amplitudes and high numbers of load cycles, symptoms of fatigue are to be expected. The same applies to high-strength steels: So derailed in 2008. ICE 3 in Cologne's main train due to breakage of the axle , which with over 10 9 had far exceeded load changes the usual limit numbers of cycles for fatigue strength.
The fatigue strength depends on the type of load that occurs. Depending on whether the type of load consists only of pressure, tension and pressure, only tension or also bending and torsion , their respective levels change. In addition, the static rest load, the so-called medium voltage , must be taken into account. It has an enormous influence on the behavior of the material. Depending on the medium voltage, one speaks of alternating strength or threshold strength:
- The alternating strength is the fatigue strength value at which the mean stress is zero.
- The threshold strength is the fatigue strength value at which the mean stress is equal to the stress amplitude.
Fatigue strength diagrams
In order to be able to read the fatigue strength both as a function of the mean stress and as a function of the deflection stress, the Wöhler curve is not suitable because it always assumes a constant mean stress. In the course of time, a large number of fatigue strength diagrams have therefore been developed, of which the Haigh diagram and the Smith diagram have established themselves in practice. The use of these two fatigue strength diagrams is also recommended in the DIN 50100 standard.
Haigh diagram
In the Haigh diagram, the deflection stress is plotted on the y-axis and the mean stress on the x-axis. For construction, the tensile strength is first entered on the y-axis and, both positive and negative, on the x-axis. These three points form the isosceles triangle characteristic of the Haigh diagram . The fatigue strength range is determined by entering the fatigue strength and the yield point . In the picture on the left, the fatigue strength range is marked in red.
The fatigue strength can now be read for any voltage ratio. For this purpose, the tension relationship with
educated.
Then the straight line assigned to this stress ratio (for examples of such straight lines see picture on the right) is followed up to the limit of the fatigue limit.
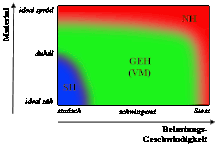
Smith Chart
Another fatigue strength diagram is the fatigue strength diagram according to Smith, or the Smith diagram for short . In the Smith diagram, the total stress is plotted against the deflection stress. The yield point , the crush limit , the tensile strength , the compressive strength and the fatigue strength are required for construction. First, the bisector is drawn. The yield point is the upper, horizontal limit line of the graph, the crush limit is the lower limit. Both straight lines end at the intersection with the bisector. Then the values for fatigue strength and swelling strength are entered and connected with curves or straight lines. If the amplitudes of the upper or lower stress for the present mean stress are within the range enclosed by the Smith chart, then fatigue strength can be assumed, otherwise not.
In order to avoid expensive material tests, it is possible to use empirical relationships between the material parameters. For the crush limit and the compressive strength, the corresponding values for tensile stress can be used for metallic materials with the opposite sign, since the amount of compressive strength is usually higher than that of the tensile strength. If the tensile strength is not known, the angle of inclination of the line connecting the tensile strength and the yield point can be taken from tables. In addition, there are approximations that relate alternating bending strength and yield strength, alternating tensile / compressive strength and yield strength as well as alternating bending strength and alternating torsional strength.
Fatigue strength
Often a component or an assembly is not designed to be durable, but rather operationally. You are in the area of fatigue strength , where only a certain number of load changes can be endured between tensile strength and fatigue strength. The number of endurance cycles of a component under operational load (variable load amplitudes) up to failure can be predicted within the scope of statistical accuracy with the help of the Wöhler curve. To do this, the methods of linear damage accumulation according to Palmgren, Langer and Miner are used. At the same time, intensive experimental tests are used to verify the computational results. Fatigue strength is used today in almost all areas of technology for the purpose of lightweight construction.
Components that are not fatigue-resistant but operationally stable require less material and therefore have a lower mass. A lighter vehicle , for example, has lower fuel consumption, a lighter structure allows a higher payload. Occasionally, the operational design also serves to fulfill the function: Durable aircraft would not be able to fly because they would be too heavy.
In reality, impact loads and environmental conditions such as temperature, pressure, corrosion, stone chips, precipitation, creep and aging of the material also flow into the consideration of operational strength. It is also important to distinguish between purpose-oriented operation and abuse. A solid component is only designed up to a certain vibration or impact amplitude and may fail after this limit load is exceeded. Ideally, a safety-relevant component fails only through deformation and not through breakage, in order to ensure residual safety and reduce the risk of an accident. Special events play a major role in the testing of components, since these stresses must be withstood by the operationally stable component without damage. However, these loads only occur in exceptional cases within the calculated service life and are not misused due to the mean amplitude strength.
Shape strength
The fatigue strength of a specific component is called structural strength. In practice, it is significantly below the fatigue strength or fatigue strength determined in the Wöhler test for a standardized sample. There are several reasons for this:
- The larger a component, the lower its structural strength. In the case of metallic materials, non-metallic inclusions caused by the manufacturing process can lead to the formation of cracks. For larger components, the absolute number of inclusions or material defects is higher. This also increases the likelihood that one of these imperfections will become a progressive crack that can lead to breakage. A shaft with a diameter of 60 mm can withstand a 20% lower deflection stress than a shaft with a diameter of 10 mm.
- Rough surfaces reduce the tolerable vibrating stress. The values determined in the Wöhler test correspond to polished surfaces. If a surface is only roughed or provided with a rolled skin , cracks can appear at the edges of the surface, which grow with every load change and thus penetrate the component. This effect is particularly pronounced in the case of high-strength steels, which have a high tensile strength but tend to break brittle . Here the tolerable deflection stress of the polished surface is sometimes twice as great as that of the surface of the semi-finished product .
- Real components contain notches, for example through undercuts or shaft shoulders. These notches lead to undesirable voltage peaks. When determining the permissible stresses, it must therefore be multiplied by the notch action number.
While the Wöhler test shows a uniaxial stress state with tensile / compressive load, in reality multi-axis stress states with bending , torsion and shear force are to be considered. In order to be able to continue using the test results of the materials testing, the equivalent stress for the respective component must be calculated. In the case of oscillating loads, the shape change energy hypothesis (GEH) is the most frequently used tool.
If a concrete component is fatigue-resistant, it is called design fatigue strength. As a rule, a Smith chart is used as the shape fatigue strength diagram, in which reductions in the safe area due to the influence of size and surface as well as the notch coefficient are entered.
Component Wöhler tests are carried out as proof of strength for components manufactured in series production as well as safety-relevant components such as bogies .
Fatigue strength improvement in welded constructions
The durability and life brandishing loaded welded metal structures is in many cases by the welds - determined - in particular the weld transitions. Targeted post-treatment of the transitions by grinding , blasting , shot peening , high-frequency hammering, etc. can significantly increase the service life of many constructions with simple means. With high-frequency hammering , the increase in fatigue strength is essentially based on the introduction of compressive residual stresses to increase the resistance to crack formation and crack propagation by superimposing the notch stresses with compressive residual stresses , a reduction in the notch effect and a strengthening of the surface layer.
literature
- J. Köhler: Zero break line of fatigue strength . In: Materials Science and Technology . tape 39 , no. 9 , 2008, p. 654–658 , doi : 10.1002 / mawe.200800326 .
- J. Köhler: Relative fatigue strength, DeGruyter Oldenbourg Verlag, 2014
- D. Munz, K. Schwalbe, P. Mayr: Long-term vibration behavior of metallic materials . Braunschweig 1971
Web links
- Pictures of tests on fatigue strength on the website of the IWM of the RWTH Aachen
- Video from the Karlsruhe University of Applied Sciences - Technology and Economics on the fatigue strength test on YouTube
Individual evidence
- ↑ a b Georg Jacobs: Machine design . Mainz Verlag, Aachen 2015, ISBN 3-86130-748-0 , p. 19-21 .
- ↑ a b Christoph Broeckmann, Paul Bite: Materials Science I . Mainz Verlag, Aachen 2014, p. 40-54 .
- ↑ Federal Institute for Materials Research and Testing: Damage analysis wheelset shaft ICE 3 on bahn-fuer-alle.de, accessed on November 22, 2015.
- ↑ Fatigue strength diagram according to Smith construction of the Smith diagram
- ↑ a b c d e Georg Jacobs: Machine design . Mainz Verlag, Aachen 2015, ISBN 3-86130-748-0 , pp. 24–42.
- ↑ Heiko Mannsbarth, Jürgen Jakob: Bogie Görlitz IX - consistent further development of proven bogie technology. ( Memento of the original from December 8, 2015 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. In: Glasers Annalen 132 (October 2008), accessed October 30, 2015.
See also
Pneumatic Impact Treatment , an HFMI process to significantly increase fatigue strength