Notch effect
The notch effect occurs on incised or notched bodies that are subjected to tension , shear or torsion . It consists of two mechanisms:
- From a local stress concentration (increase in stress ) - is described by the shape number .
- As a support effect - the material and the specific decay behavior of the stress concentration counteract the stress peaks and thus reduce the damage effect (expressed by the support number according to DIN 743 :) .
The notch action number is defined as the quotient of the shape number and the supporting number:
Technical importance
The notch effect is often undesirable because it places higher demands on components in technical applications, so that they have to be built larger in order to achieve their intended service life or otherwise fail prematurely. On the other hand, the notch effect is used in a targeted manner.
- See also: Notch strength
Targeted application
- Relief notches: An additional notch can guide the flow of force past a heavily stressed area. The picture on the right illustrates the effect. The red arrows show the power flow. In the example (picture on the left), a sharp shoulder is required for structural reasons, which is associated with high notch stresses. The component is alternately loaded and will break at this shoulder (red circle) because it represents the weak point. An additional notch (picture on the right) with a large radius gently deflects the flow of force onto the smaller, lower cross-section. The maximum stress in the component is reduced and the load-bearing capacity increases instead of decreasing. Relief notches can also occur unintentionally, for example when cutting glass .
- In order to allow an unavoidable break to occur only at a certain point in the event of overload, notches are placed as predetermined breaking points . During the construction, care is then taken to ensure that the break point is easily accessible and the damaged component can be replaced inexpensively, and that further damage risks are avoided.
- Scoring glass , ceramic and other brittle materials in order to break them along the notch. A layperson's attempt to improve the effectiveness of the scribe by repeating the process has the opposite effect. Relief notches appear and the material breaks worse.
- Packaging, such as B. Food cans or beverage cans with pull-tabs or foil packaging are provided with pre-cut notches to make opening easier
Notch effect as a disruptive factor and countermeasures
Notches that lead to unwanted failure can have a number of causes:
- Many natural processes leave notches, such as B. Rust on the surface of steel components. The structure of such constructions is weakened; as the damage progresses, a crack spontaneously terminates the load-bearing capacity.
- The notch effect is based on rough surfaces. You can often counteract it with smoothed or polished surfaces.
- Inclusions in the body, e.g. B. blowholes or graphite in gray cast iron act as notches.
- The type of joining process, e.g. B. riveting instead of gluing influences the notch effect at the seam.
- The geometry of the component can create a notch effect, e.g. B. a shaft shoulder or a change in the cross section of rotationally symmetrical (round) components.
- Due to their geometric shape and tensile stresses due to the cooling process, weld seam transitions have a strong notch effect. This can be reduced very effectively by machining with high-frequency hammers.
mechanism
The six pictures show how the notch effect is created:
- Starting position: A normal round bar that is not loaded and has a cylindrical shape.
- If a tensile force is applied to the ends along the component axis, the rod will elongate under the influence of the tensile force. At the same time it contracts transversely to the direction of pull (red arrows) ( transverse contraction ).
How much it contracts in the transverse direction, is the Poisson's ratio ( Poisson described):- Some materials expand when pulled ( <0)
- Many utility materials are constricted in such a way that the volume remains approximately constant (perfect volume constancy corresponds to = 0.5)
- If you weld a sleeve to the round bar (highlighted in yellow) and put a tension on it again, nothing essential changes in the circumstances. Here, too, the rod contracts in the transverse direction.
- However, if the sleeve with the round rod were firmly (cohesively) connected over the entire length or - which would be analogous in terms of the effect - the tension rod is notched, additional stresses result. The yellow marked zones are not stretched by the tensile force in the longitudinal direction, so they do not contract in the transverse direction. On the other hand, the core material (highlighted in gray), which transmits the tensile force, wants to contract inwards (red arrows). However, the yellow marked zones do not sag and instead generate a transverse force that is directed outwards and tries to prevent the core material from transversely contracting .
- Here, the stress distribution is shown in a round bar that is subjected to tensile load. The stresses are distributed fairly evenly over the entire cross-section.
- If you choose a thicker tension rod and provide it with a groove so that the remaining cross-section has the same diameter as the previous round rod, then there is an excessive increase in stress at the transition points. In this situation, not only are tensile stresses created in the longitudinal direction, but the notch also creates tensile stresses in the transverse direction. The load-bearing core material is additionally loaded and the now multi-axis stress state leads to local stress peaks. The shaft with the notch is therefore less stable than the unnotched, narrow round rod, although it has more material and the same diameter in the narrowest cross-section.
If one assumes that the largest diameter and the smallest diameter are in Figure (4) , this notched bar will tear at lower tensile stresses than a bar that has only one diameter over its entire length .
How much a notch increases the tension depends solely on the shape of the notch. Pointed or deep notches look stronger than well-rounded or shallow notches.
The local damaging effect depends on the material and the type of load.
- The material can be particularly sensitive to notch influences; this applies in particular to brittle materials. Tough ( ductile ) materials, on the other hand, can relieve stress peaks through plastic deformation (flow). Furthermore, materials such as lamellar cast iron are extremely insensitive to additional notches due to their special structure, as it is already full of notches due to its structure and therefore extremely brittle in itself.
- The uniaxial loads include static, swelling tensile loads or alternating loads (alternating tension and compression). Multi-axis loading cases can combine tension / compression, bending or torsion.
calculation
The calculation of notches in the course of the load capacity calculation of shafts is standardized in DIN-743 (Part 1–4). Two variables are relevant for the design of components taking into account the notch effect: the shape number and the notch effect number . The shape number is defined as the ratio of excessive stress to the nominal stress, the notch coefficient as the ratio of the deflection stresses of the unnotched and notched specimen.
Shape number
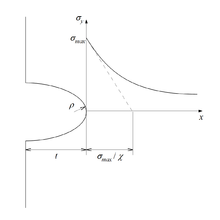
In contrast to a flat tension rod, the stress curve in the cross-section of a notch is not linear. At the edges there are voltage peaks, some of which are many times higher than the nominal voltage. To compensate for this, the actual stress in the center of the cross-section is less than the nominal stress. The shape number now relates the highest stress in the notch to the nominal stress:
It is
- the voltage spike
- the nominal voltage.
The number of forms depends on the geometry of the workpiece. It applies here
- .
is a geometry function that is different for each notch. Even for simple geometries, it usually assumes complex relationships. In practice, the number of shapes is usually not calculated by hand, but read from diagrams printed in tables. Such a diagram is shown in the adjacent picture. On the abscissa the ratio of the notch radius is ablated to the shaft diameter, on the ordinate the form number . The blue, superimposed lines represent the ratio of the diameters at the diameter transition at the shaft shoulder. Higher-lying lines represent higher diameter transitions. It can be seen that the number of shapes assumes particularly large values with sharp notch radii and large diameter transitions. Consequently, shallow notches and small diameter transitions, possibly implemented in several steps, are good solutions for the construction of components.
Shape numbers can also be determined using the finite element method (FEM). The same applies to optical stress examinations and strain measurements. If the support number is known, the notch effect can be determined for the specific application.
Notch effect number
The notch coefficient is used to design components that are subject to vibrations . For the determination, a notched and an unnotched sample are subjected to a Wöhler test. With the same deflection stress, the notched specimen usually breaks after a lower number of load cycles, since the notch becomes the starting point of a crack . As a result, the fatigue strength of the smooth specimen is at higher deflection stresses than that of the notched specimen. The ratio of these two deflection stresses is defined as the notch coefficient. It applies
.
Where:
- the deflection stress that leads to fatigue strength in an unnotched specimen
- the deflection stress that leads to fatigue strength in a notched specimen.
While the shape number is a purely geometric variable, the notch number is defined by the results of empirical tests and depends on the tensile strength of the material used.
Web links
- Strength condition for oscillating loads with notch effect (accessed on October 14, 2019)
- Contribution to the determination of the notch effect on splined shafts with free and bound outlet (accessed on October 14, 2019)
- Axles and shafts: Proof of load capacity according to DIN 743 (accessed on October 14, 2019)
- Base load types (accessed on October 14, 2019)
- Notch effect on splined shaft connection with involute tooth profile (accessed on October 14, 2019)
literature
- The main work in this area is based on Heinz Neuber , who published the first edition of his book in 1937. Heinz Neuber: Notch stress theory . 4th edition. Springer Verlag, Berlin, Heidelberg 2001, ISBN 978-3-642-63199-3 .
- DIN 743-2: Load capacity calculation of shafts and axles - Part 2: Form numbers and notch action numbers.
Individual evidence
- ↑ a b c d e Christoph Broeckmann, Paul Beiss: Materials Science I . Institute for Material Applications in Mechanical Engineering at RWTH Aachen University , Aachen 2014, pp. 69–79.
- ↑ Calculating notches - calculate notch stress. In: www.maschinenbau-wissen.de. Retrieved February 7, 2016 .
See also
Pneumatic Impact Treatment - a High Frequency Mechanical Impact (HFMI) method to reduce the notch effect at the seam transition