Spin-orbit coupling

The spin-orbit coupling or spin-orbit interaction is an interaction that occurs in atomic, nuclear and elementary particle physics, the strength of which depends on the position of the particle's spin relative to its orbital angular momentum . In the case of bound particles, the spin-orbit interaction leads to a splitting of energy levels, which contributes to the fine structure of the level scheme. These effects are relatively minor for the electrons in the atomic shell, but they have important effects on the structure of the atom.

The spin-orbit interaction is expressed in the context of non-relativistic quantum mechanics by a separate term in the Schrödinger equation, which contains the scalar product of the orbital and spin angular momentum of the particle. In relativistic quantum mechanics , a corresponding energy contribution results automatically.

Bound particles

The spin-orbit interaction was first observed with the electrons in the atomic shell. Here it causes a splitting of the spectral lines and thus contributes (in addition to relativistic effects and the Darwin term ) to the fine structure of the atomic spectra. A well-known case is the splitting of the yellow D-line of sodium , which can be observed with a good prism.

The spin-orbit interaction for the protons and neutrons in the atomic nucleus is much stronger (see shell model (nuclear physics) ).

Semi-classical interpretation for an electron

If one takes the intrinsic angular momentum (spin) and magnetic moment of the electron as given, the spin-orbit coupling can already be explained clearly in Bohr's atomic model : From Maxwell's theory and the special theory of relativity it follows that an electron occurs when it is in the electric field of an atomic nucleus circles, a magnetic field acts. In the rest system of the electron, a circular movement of the nucleus is perceived. Due to the charge of the nucleus, this movement represents a circular current which, according to Biot-Savart's law, generates a magnetic field parallel to the orbital angular momentum vector. The magnetic field caused by the circular current corresponds in this classic view to the magnetic moment of the orbital angular momentum. In addition, there is the spin of the electron (intrinsic quantity), which also causes a magnetic moment. These magnetic moments can now interact with one another. Imagine a bar magnet, which represents the spin, in the field of a coil, which represents the field due to the circular motion. There is an energetically favorable alignment in which the field of the bar magnet is parallel to the field of the coil, and an unfavorable one in which the field of the bar magnet is antiparallel to the field of the coil. Since the magnetic moment of the electron is antiparallel to its spin, there is a higher energy for one spin direction parallel to the field and a lower one for the opposite one. Since only these two setting options exist for a spin 1/2, a single energy level is split into two levels, and there are two lines in the optical spectra that are slightly shifted compared to the original position, but which appear as one when viewed roughly.

In non-relativistic quantum mechanics, a corresponding summand is added to the Schrödinger equation for each electron ; in relativistic quantum mechanics, spin, magnetic moment and spin-orbit interaction result automatically from the Dirac equation .

Spin-orbit coupling energy for an electron

The operator for the spin-orbit interaction of an electron in the central electrostatic field is

${\displaystyle {\hat {H}}_{\ell s}=-{\hat {\vec {B}}}_{\ell }\cdot {\hat {\vec {\mu }}}_{s}={\frac {a}{\hbar ^{2}}}{\hat {\vec {\ell }}}\cdot {\hat {\vec {s}}}}$

Therein is the spin-orbit coupling constant ${\displaystyle a}$

${\displaystyle a={\frac {Ze^{2}\mu _{0}\hbar ^{2}}{8\pi m_{e}^{2}r^{3}}}}$,

which depends on the strength of the magnetic field caused by the orbital motion of the electron and its magnetic moment . ${\displaystyle B_{\ell }}$ ${\displaystyle {\vec {\mu }}_{s}}$

${\displaystyle m_{e}}$describes the electron mass, the electron charge, the magnetic field constant and the reduced Planck quantum , the distance between the electron and the atomic nucleus. ${\displaystyle e}$ ${\displaystyle \mu _{0}}$ ${\displaystyle \hbar }$ ${\displaystyle r}$

This results in the following energy shift for states : ${\displaystyle \ell >0}$

${\displaystyle \Delta E=-{\vec {\mu }}_{s}\cdot {\vec {B}}_{l}=a{\frac {{\hat {\vec {\ell }}}\cdot {\hat {\vec {s}}}}{\hbar ^{2}}}={a \over 2}\;[j(j{\mathord {+}}1)-\ell (\ell {\mathord {+}}1)-s(s{\mathord {+}}1)]=\left\{{\begin{array}{ccc}{\frac {a}{2}}\ell &({\text{für}}\ j=\ell +{\frac {1}{2}})\\-{\frac {a}{2}}(\ell +1)&({\text{für}}\ j=\ell -{\frac {1}{2}})\end{array}}\right.}$

${\displaystyle j}$is the quantum number of the total angular momentum of the particle, which is quantized in half-integer multiples of . Since the level is degenerate , its weighted center of gravity remains unaffected by the spin-orbit splitting (rule of spectroscopic stability ). In Bohr's model is the orbital radius of the electron, ( principal quantum number , Bohr radius ). Therefore is greatest for the innermost Bohr orbit ( ). Overall, the splitting through spin-orbit coupling grows with increasing atomic number, so like . In quantum mechanical treatment, the factor is to be replaced by the mean value taken over the respective orbital . If the influences of other electrons are neglected, the result is ${\displaystyle \hbar }$ ${\displaystyle 2j+1}$ ${\displaystyle r}$ ${\displaystyle r=n^{2}{\tfrac {a_{B}}{Z}}}$ ${\displaystyle n}$ ${\displaystyle a_{B}}$ ${\displaystyle a}$ ${\displaystyle n=1}$ ${\displaystyle Z}$ ${\displaystyle Z^{4}}$ ${\displaystyle {\tfrac {1}{r^{3}}}}$ ${\displaystyle \left\langle {\tfrac {1}{r^{3}}}\right\rangle }$

${\displaystyle \left\langle {\frac {1}{r^{3}}}\right\rangle ={\frac {Z^{3}}{a_{B}^{3}\,n^{3}\,(\ell +1)(\ell +{\frac {1}{2}})\ell }}}$

The distance between the split levels to amounts (see also Landé interval rule ). He occurs z. B. in X-ray photoelectron spectroscopy (XPS) , in the absorption of X-rays and the emission of characteristic X-rays , because these processes depend directly on the binding energy of individual electrons in the inner shells of the atom. ${\displaystyle j=\ell \pm {\tfrac {1}{2}}}$ ${\displaystyle \Delta E={a \over 2}(2\ell +1)}$

Coupling schemes for several particles

If the total angular momentum of the atom is made up of the spins and orbital angular momenta of at least two particles ( ) , there are various possibilities to form intermediate sums of the angular momentum with their own quantum numbers. These possibilities are referred to as a coupling scheme. The most important ones are coupling with quantum numbers for the total angular momentum of each individual particle, and coupling with quantum numbers and for the sum of orbital angular momenta or spins of all particles. In principle, each multi-electron state can optionally be represented by superimposing basic states or basic states. Advanced calculations of the structure of the energy eigenstates of the atomic shell always assume such an intermediate coupling scheme . ${\displaystyle s_{i}}$ ${\displaystyle \ell _{i}}$ ${\displaystyle i=1,2,\ldots }$ ${\displaystyle jj}$ ${\displaystyle j_{i}}$ ${\displaystyle LS}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle jj}$ ${\displaystyle LS}$

jj coupling with multiple electrons

For each particle , the spin and orbital angular momentum are added and result in its total angular momentum with quantum number . The total angular momentum of the electron shell with quantum number is formed from these 1-particle total angular momentum . If there are more than two particles, there are again several possibilities, but they have not been given their own names. ${\displaystyle i}$ ${\displaystyle j_{i}}$ ${\displaystyle j_{i}}$ ${\displaystyle J}$

The coupling scheme results in states which, given a strong spin-orbit interaction, represent a good approximation of the energy eigenstates of the atom. In the atoms decreases the strength of the spin-orbit interaction with increasing principal quantum number from, with increasing (for. Example, in lead with ) but at. In the case of medium-weight atoms in the inner shells and in the case of heavy atoms in the entire shell, it often plays a greater role than the mutual interference between the electrons. Every electron is therefore in a state with a “good quantum number” for its total angular momentum. When the angular momentum of the individual electrons is combined to form the total angular momentum of the atom, the total angular momentum of a closed shell or subshell is always zero. Therefore, for the total angular momentum of the atomic shell, only the electrons in not fully occupied shells have to be taken into account. ${\displaystyle jj}$ ${\displaystyle n}$ ${\displaystyle Z}$ ${\displaystyle Z=82}$ ${\displaystyle j_{i}}$ ${\displaystyle j_{i}}$ ${\displaystyle J}$

LS coupling with several electrons

A total orbital angular momentum with quantum number is formed from the orbital angular momentum of all particles , as well as a total spin with quantum number from the spins . The total angular momentum of the electron shell with quantum number is formed from and . Due to its name , the -coupling is mistakenly associated with, or even confused with, the spin-orbit interaction. Sometimes the coupling is also known as the Russell-Saunders coupling , named after Henry Norris Russell and Frederick Albert Saunders . ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle J}$ ${\displaystyle LS}$ ${\displaystyle LS}$

The heat- prevails when the spin-orbit interaction can be neglected. That means and are good quantum numbers, or to put it another way, and still commute approximately with the Hamiltonian of the system. This applies to the natural energy states of the lighter atoms, in which the mutual electrostatic disturbance of the electrons plays a greater role than the spin-orbit interaction of each individual electron. The above-described dependence of the energy of each individual electron on the scalar product is so weak for smaller atomic numbers Z that the electrons in a non-closed shell are primarily influenced by their mutual Coulomb repulsion, which is independent of the spins. The total wave function of an energy eigenstate is therefore to be applied as a good approximation as a product of a spatial wave function of all electrons with a spin function of all electrons. In such states (except for ) no electron has a state that is characterized by a quantum number for its total angular momentum. However, the total orbital angular momentum has ${\displaystyle LS}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle ({\hat {\vec {\ell }}}\cdot {\hat {\vec {s}}})}$ ${\displaystyle \ell {\mathord {=}}0}$ ${\displaystyle j}$

${\displaystyle {\hat {\vec {L}}}=\sum _{i}{\hat {{\vec {\ell }}_{i}}}}$

a fixed quantity (quantum number , eigenvalue for the operator ), which also determines the energy of these states. Since the energy does not depend on the spins in this approximation, it is always a question of degenerate states of the same , which can be further broken down formally according to the quantum number for the total spin of the electrons: ${\displaystyle L}$ ${\displaystyle \hbar ^{2}L(L{\mathord {+}}1)}$ ${\displaystyle {\hat {\vec {L}}}^{2}}$ ${\displaystyle L}$ ${\displaystyle S}$

${\displaystyle {\hat {\vec {S}}}=\sum _{i}{\hat {{\vec {s}}_{i}}}}$.

(In fact, one does not need to take into account closed shells, because they automatically have .) If at least two electrons are in the same subshell , then and each can have several different values. If the Coulomb repulsion and other energy contributions are - still - neglected, they all belong to the same energy ( degeneracy ). However, only those combinations of and occur that correspond to the Pauli principle , i.e. H. which result in an antisymmetric wave function when two electrons are exchanged. Now the spatial wave functions of two electrons are always either symmetric or antisymmetric , depending on whether they are even or odd when interchanged (within a subshell) . The spin wave function for a given total spin is either symmetric or antisymmetric, only in the opposite sense. In order that a fermionic antisymmetric wave function arises, the position and spin functions of a level must have opposite symmetry. ${\displaystyle L{\mathord {=}}S{\mathord {=}}0}$ ${\displaystyle n,\ell \ (\ell \neq 0)}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle L}$ ${\displaystyle L}$ ${\displaystyle S}$

If the Coulomb repulsion of the electrons is taken into account in the next step, the energy of the state is increased. This energy contribution is different for the spatial wave functions for different total orbital angular momenta , in particular the repulsion for a symmetrical spatial wave function ( even) is greater than for antisymmetric ( odd). The energy therefore depends on the symmetry character of the spatial wave function, which, as just shown, must be the opposite of the symmetry character of the respective spin function. In the end, this results in a different energy for each value of , although the spins of the electrons have not yet been mathematically involved in the interactions. For light atoms (up to about the atomic number ) this is a good approximation. The quantum numbers and can thus be assigned to the levels of light atoms . This is the coupling scheme. In a certain sense it is the opposite of -coupling (but the states formed after -coupling are not automatically orthogonal to the states formed after -coupling). ${\displaystyle L}$ ${\displaystyle L}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle Z=10}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle LS}$ ${\displaystyle jj}$ ${\displaystyle LS}$ ${\displaystyle jj}$

In the following step the still existing spin-orbit coupling of each electron is taken into account. It makes itself noticeable in the -states through a further fine splitting, through which a slightly different energy is assigned to each possible eigenvalue of the total angular momentum (as if there were an interaction of the form ). The result is a multiplet with (generally) closely adjacent levels in their quantum numbers and all agree. ${\displaystyle LS}$ ${\displaystyle J}$ ${\displaystyle {\hat {\vec {J}}}{\mathord {=}}{\hat {\vec {L}}}{\mathord {+}}{\hat {\vec {S}}}}$ ${\displaystyle ({\hat {\vec {L}}}\cdot {\hat {\vec {S}}})}$ ${\displaystyle {2S{\mathord {+}}1}}$ ${\displaystyle L}$ ${\displaystyle S}$

In the case of coupling, every electron still has the quantum numbers , but not . One level of the entire atomic shell has the three quantum numbers , which are summarized in the term symbol . ${\displaystyle LS}$ ${\displaystyle n_{i},\ell _{i}}$ ${\displaystyle j_{i}}$ ${\displaystyle L,S,J}$ ${\displaystyle ^{2S{\mathord {+}}1}L_{J}}$

As the atomic number increases, the description after coupling becomes an increasingly poor approximation, until, from medium atomic numbers, the spin-orbit interaction of the individual electrons becomes so great that the coupling scheme is increasingly applicable. They say the coupling is broken. The transition region between the two coupling schemes is (engl. As an intermediate coupling intermediate coupling ), respectively. It is characterized, for example, by a relaxation of the intercombination ban. ${\displaystyle LS}$ ${\displaystyle jj}$ ${\displaystyle LS}$

Splitting in a magnetic field

Hydrogen levels and spin orbit interaction under the influence of a magnetic field.

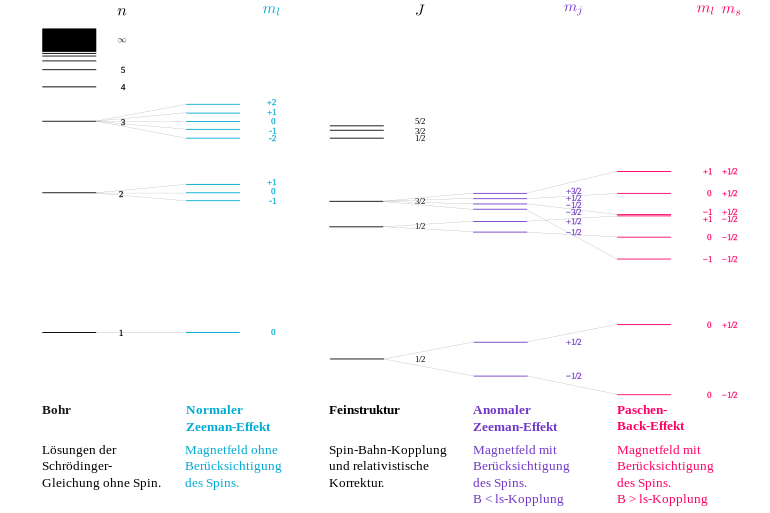
A level with certain things , and contains individual states with different things . Without a magnetic field they are energetically degenerate and form a single level. With a finite magnetic field this no longer applies: ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle J}$ ${\displaystyle 2J+1}$ ${\displaystyle M_{J}}$ ${\displaystyle \in \{-J\,,-J+1,\,...\,,\,+J\},}$

• In a weak magnetic field to keep the three quantum numbers , and its meaning, but the energy splitting of the on. There arise levels (with the same , , ). The additional magnetic energy of these energy eigenstates is proportional to the magnetic field and to (see Zeeman effect and Landé factor ). ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle J}$ ${\displaystyle M_{J}}$ ${\displaystyle 2J+1}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle J}$ ${\displaystyle \Delta E_{M_{J}}}$ ${\displaystyle B}$ ${\displaystyle M_{J}}$
• If this split becomes so large that it is no longer negligible compared to the energy difference to the levels with neighboring values, the coupling from and to a fixed value is increasingly broken. The energy eigenstates then still have the quantum numbers and , but are superpositions of the states with different things , so they no longer have a fixed quantum number . Their energies vary non-linearly with the magnetic field until, in the extreme case of the strong field ( Paschen-Back effect ), the states become fixed values and natural energy states and their energies again depend linearly on the magnetic field. ${\displaystyle J}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle J}$ ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle J}$ ${\displaystyle J}$ ${\displaystyle M_{L}}$ ${\displaystyle M_{S}}$

The same happens with a single external electron with a certain , and . While in the weak magnetic field all levels show their Zeeman splitting proportionally , the levels in the strong magnetic field change into states of fixed quantum numbers and over (see figure). ${\displaystyle \ell }$ ${\displaystyle s}$ ${\displaystyle j}$ ${\displaystyle j}$ ${\displaystyle m_{j}}$ ${\displaystyle m_{s}}$ ${\displaystyle m_{\ell }}$

Unbound Particles

For example, if a particle is scattered and thereby deflected from its flight direction, the spin-orbit interaction generally causes the differential cross-section to depend on the azimuth angle (see also spin polarization , Mott scattering ). The spin-orbit interaction also plays a corresponding role in nuclear reactions and for all elementary particles with strong interaction ( hadrons ).

Web links

• Uni Stuttgart spin-orbit interaction in the hydrogen atom

References and footnotes

1. ^ Hermann hook , Hans Christoph Wolf : atomic and quantum physics. Introduction to the experimental and theoretical basics. 8th, updated and expanded edition. Springer, Berlin et al. 2004, ISBN 3-540-02621-5 .
2. ↑ Hermann Haken, Hans Christoph Wolf: Atomic and Quantum Physics - Introduction to the experimental and theoretical basics . 8th edition. Springer, Berlin 2003, ISBN 3-540-02621-5 , pp. 329 .