Anomalous diffusion

Mean square displacement for normal, super and sub diffusion ${\displaystyle \langle r^{2}(\tau )\rangle }$

In statistical physics, anomalous diffusion is a special type of the diffusion transport process or Brownian molecular movement that occurs in many complex (e.g. viscoelastic ) media. It cannot be described by the usual ( Fick's ) law of diffusion. In contrast to normal diffusion, the mean square displacement of an anomalous diffusing particle, i.e. the space that the particle traverses in time , does not increase proportionally , but typically follows a power law with the anomaly parameter α. Anomalous diffusion describes random movements with long-range correlations for which the central limit theorem of statistics no longer applies. Such transport processes occur, for example, in cells or in people's travel behavior. ${\displaystyle \langle r^{2}(\tau )\rangle }$ ${\displaystyle \tau }$ ${\displaystyle \tau }$ ${\displaystyle \langle r^{2}(\tau )\rangle \propto \tau ^{\alpha }}$

Definition and characteristics

definition

Usual diffusion processes can be macroscopically described by Fick's diffusion equation. Microscopically, this description changes into a Brownian molecular movement ( Wiener process ), with the mean square displacement:

${\displaystyle \langle \Delta r^{2}(\tau )\rangle _{\text{normale Diffusion}}=2n\cdot D\cdot \tau }$

The factor indicates the number of spatial dimensions and the parameter D is the diffusion coefficient . ${\displaystyle n}$

Anomalous diffusion, on the other hand, is characterized by the following dependency:

${\displaystyle \langle \Delta r^{2}(\tau )\rangle _{\text{anomale Diffusion}}=2n\cdot K_{\alpha }\cdot \tau ^{\alpha },\quad \alpha >0}$

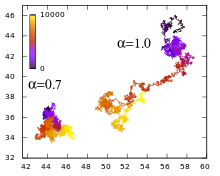
Here is a generalized diffusion coefficient and the anomaly parameter. The unit of this generalized diffusion coefficient is , therefore, depends on the anomaly parameter. A distinction is made between two regimes, which are also shown in the figure at the top: ${\displaystyle K_{\alpha }}$ ${\displaystyle \alpha }$ ${\displaystyle [K_{\alpha }]=m^{2}/s^{\alpha }}$

• Subdiffusion ( ): ${\displaystyle 0<\alpha <1}$ This type of slowed down diffusive movement can be observed inside cells and during random walks on fractal structures.
• The special case describes the usual normal diffusion . ${\displaystyle \alpha =1}$
• Superdiffusion ( ): ${\displaystyle \alpha >1}$ This accelerated diffusion occurs e.g. B. on Lévy flights , or when moving bills or people traveling.
• The special case is ballistic diffusion (English ballistic diffusion called). This corresponds to a case where, in addition to the diffusion movement, there is also a drift. ${\displaystyle \alpha =2}$

Anomalous diffusion as a macroscopic effect

Anomalous diffusion in itself is first of all a macroscopic effect. As the various examples above show, it is not easy to derive the microscopic cause of the anomalous diffusion.

Time-dependent diffusion coefficient and memory

The mean quadratic displacement can also be expressed formally by a time-dependent diffusion coefficient : ${\displaystyle D_{\alpha }(\tau )}$

${\displaystyle \langle \Delta r^{2}(\tau )\rangle _{\text{anomale Diffusion}}=2n\cdot D_{\alpha }(\tau )\cdot \tau \quad {\text{mit}}\quad D_{\alpha }(\tau )=K_{\alpha }\cdot \tau ^{\alpha -1}}$

The diffusion coefficient is no longer constant over time, the behavior (the "diffusion speed") of a particle depends on how long it has been moving (for subdiffusion, for example, the longer it moves, the slower it becomes). This means that there is a kind of memory in the system that makes the current movement dependent on the previous history. A more detailed mathematical model for this is described below in the section Anomalous Diffusion and the Langevin Equation .

Occurrence of abnormal diffusion

Anomalous diffusion phenomena occur in different systems. Some examples are to be summarized here, some of which are explained in more detail in the rest of the article:

• Superdiffusion with : ${\displaystyle \alpha >1}$
  • in the theoretical random walk model of the Lévy flight
  • when moving bills or people traveling. Traveling people remain z. B. typically for some time in a city and move there on a small spatial scale. With a certain (low, but not negligible) probability they will then take a trip to a distant city, which leads to a big jump. Lévy flights are a theoretical model for such behavior.
  • Movement of individual cells in cell aggregates

• Subdiffusion with : ${\displaystyle 0<\alpha <1}$
  • In the interior of cells , subdiffusion is observed in the movement of macromolecules through the cytoplasm . One reason for this can be what is known as molecular crowding, i.e. the presence of many (tightly packed) macromolecules and organelles in the cytoplasm
  • Abnormal diffusion is also observed on membranes of cells. The cell membrane is a complex system made up of many different building blocks (see e.g. liquid mosaic model ).
  • Random walks on fractal structures such as percolation clusters . This can also be experimentally by NMR - Diffusivitätsmessungen are shown in porous systems.
  • Diffusion in polymer networks
  • The monomer movement of long polymers such as DNA also shows the characteristic of anomalous diffusion on limited time scales, here triggered by the restricted internal movement of the polymer (see e.g. the simple Rouse model for polymer dynamics).
  • Charge carrier transport in amorphous semiconductors

Theoretical description through random walks

Normal diffusion

1000 steps of a normal-diffusive (α = 1) random walk

As already mentioned, certain random walk processes show an abnormally diffusive behavior. The progression of the movement (here in the example one-dimensional) is described in discrete time steps . The position jump from one time step to the next is Gaussian distributed for normal diffusion : ${\displaystyle \Delta t}$ ${\displaystyle \Delta x=x_{t}-x_{t-1}}$

${\displaystyle p(\Delta x)\propto \exp \left(-{\frac {1}{2}}\cdot {\frac {\Delta x^{2}}{2D\cdot \Delta t}}\right)}$

This characteristic Gaussian distribution is valid for many processes due to the central limit theorem of statistics. If, however, as in the following examples, its prerequisites are no longer met (e.g. because the variance (stochastics) of the above distribution can no longer be defined), then one can observe abnormally diffusive behavior. ${\displaystyle \sigma ^{2}=2D\cdot \Delta t}$

Levy flights

A Lévy flight with its increased probability of long jumps shows superdiffusion (α> 1). The picture also shows 1000 steps and you can clearly see the rare long jumps.

Anomalous superdiffusion occurs in random walk processes in which the jump length distribution is end-heavy . The central limit theorem no longer applies here , since the variance of end-load distributions diverges. One example are the Lévy flights already mentioned, in which very long jumps can rarely occur (but more often than in a Gaussian distribution). The jump length distribution decreases here with a power law:

${\displaystyle p(\Delta x)\propto |\Delta x|^{-(1+2/\alpha )},\alpha >1,\ \ \ {\text{für}}\ \ \ \Delta x\rightarrow \infty }$

The picture on the right shows some steps in such a process. The rare large jumps are easy to see.

Continuous time random walks (CTRW)

Another random walk process with abnormally diffusive characteristics are so-called continuous time random walks (CTRW). The movement is not divided into time steps of the same length ; instead, if the jump length remains the same , the waiting time between two jumps is considered from a distribution. This can also be understood as diffusion on a grid with traps, whereby the traps can hold the diffusing particle for different lengths of time. Is the waiting time distribution final, i.e.: ${\displaystyle \Delta t}$ ${\displaystyle \Delta x}$

${\displaystyle p(\Delta t)\propto \Delta t^{-(1+\alpha )},0<\alpha <1,\ \ \ {\text{für}}\ \ \ \Delta t\rightarrow \infty }$

this also leads to anomalous subdiffusion with anomaly parameters . ${\displaystyle \alpha }$

Continuous theoretical models

Anomalous diffusion and the Langevin equation

Normal (α = 1) and subdiffusive (α = 0.7) motion of a particle. For a detailed description of the algorithm for calculating the image, see Ref. The progress of time (10000 steps) is coded as color (see color bar at top left)

Normally diffusing particles in a viscous medium can be described using the Langevin equation :

${\displaystyle m\cdot {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-\xi \cdot {\frac {\mathrm {d} x}{\mathrm {d} t}}+F_{\text{st}}(t)}$

Here x (t) is the particle location at time t , ξ the coefficient of friction and F _st a stochastic force with vanishing correlation , i.e. white noise . This stochastic differential equation can be generalized to the fractional Langevin equation : ${\displaystyle \langle F(t)\cdot F(t')\rangle \propto \delta (t-t')}$

${\displaystyle m\cdot {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-\xi \cdot \int \limits _{-\infty }^{t}K(t-t'){\frac {\mathrm {d} x(t')}{\mathrm {d} t}}\;\mathrm {d} t+F_{\text{st}}(t)}$

There is now a so-called memory kernel , which induces a (also long-range) temporal coupling. The motion of the particle also depends on its past (integral ), which was not the case with normal Brownian motion (this corresponds to a non-Markovian random walk). If one now specifically assumes a power law for , that is ${\displaystyle K(\tau )}$ ${\displaystyle \int _{-\infty }^{t}...}$ ${\displaystyle K(\tau )}$

${\displaystyle K(\tau )\propto \tau ^{-\alpha }}$

so an anomalous mean square displacement with anomaly α also follows from this approach. With this approach one can model anomalous diffusion as it occurs in viscoelastic media . Alternatively, the stochastic term can be correlated, for example . This corresponds to a diffusion with obstacles , which is also an anomalous subdiffusion for time scales in which, on the one hand, the obstacle size and, on the other hand, the mean obstacle distance do not vanish compared to diffused distances. ${\displaystyle \langle F(t)\cdot F(t')\rangle \propto \exp(-|t-t'|)}$

Fractional diffusion equation

With the help of the fractional integro-differential operators defined in fractional infinitesimal calculus , the Fokker-Planck equation , which is often used to model normal diffusion phenomena, can be extended to anomalous diffusion. This (then fractional) differential equation describes the time development of the probability of the presence of diffusing particles at the location at the time . ${\displaystyle W(x,t)}$ ${\displaystyle x}$ ${\displaystyle t}$

${\displaystyle {\frac {\partial W(x,t)}{\partial t}}=K_{\alpha }\cdot \mathbb {D} _{t}^{1-\alpha }{\frac {\partial ^{2}W(x,t)}{\partial x^{2}}}}$

The Riemann-Liouville operator is clearly defined as the -th derivative of the function with respect to time using the integral representation: ${\displaystyle \mathbb {D} _{t}^{1-\alpha }f(t)}$ ${\displaystyle \alpha }$ ${\displaystyle f(t)}$

${\displaystyle \mathbb {D} _{t}^{1-\alpha }f(t)={\frac {1}{\Gamma (\alpha )}}{\frac {\partial }{\partial t}}\int \limits _{0}^{t}{\frac {f(t')}{(t-t')^{1-\alpha }}}\;\mathrm {d} t'}$

Here is the gamma function . The solution of this fractional differential equation leads again to the anomalous mean square displacement: ${\displaystyle \Gamma (x)}$

${\displaystyle \langle r^{2}(\tau )\rangle ={\frac {2K}{\Gamma (1+\alpha )}}\cdot \tau ^{\alpha }}$

See also

• Broken Brownian motion

literature

• Ralf Metzler, Joseph Klafter: The random walk's guide to anomalous diffusion: a fractional dynamics approach . In: Physics Reports . 339, No. 1, December 2000, pp. 1-77. doi : 10.1016 / S0370-1573 (00) 00070-3 .
• Rainer Klages, Günter Radons, Igor M. Sokolov (editors) Anomalous Transport , John Wiley & Sons, 2008, ISBN 978-3-527-40722-4

Web links

• DH Rothman (2011): MIT lecture script "Anomalous Diffusion" (accessed November 11, 2012; PDF; 224 kB)

Individual evidence

1. ↑ ^{a b c d e f g h} Ralf Metzler, Joseph Klafter: The random walk's guide to anomalous diffusion: a fractional dynamics approach . In: Physics Reports . 339, No. 1, December 2000, pp. 1-77. doi : 10.1016 / S0370-1573 (00) 00070-3 .
2. ↑ Valery Ilyin, Itamar Procaccia, Anatoly Zagorodny: Stochastic processes crossing from ballistic to fractional diffusion with memory: Exact results . In: Physical Review E . 81, No. 3, March 2010. doi : 10.1103 / PhysRevE.81.030105 .
3. ↑ Dirk Brockmann, Fabian Theis: Money Circulation, Trackable Items, and the Emergence of Universal Human Mobility Patterns . In: IEEE Pervasive Computing . 7, No. 4, October 2008, pp. 28-35. doi : 10.1109 / MPRV.2008.77 .
4. ↑ D. Brockmann: Anomalous diffusion and the structure of human transportation networks . In: The European Physical Journal Special Topics . 157, No. 1, April 2008, pp. 173-189. doi : 10.1140 / epjst / e2008-00640-0 .
5. ↑ Arpita Upadhyaya, Jean-Paul Rieu, James A. Glazier, Yasuji Sawada: Anomalous diffusion and non-Gaussian velocity distribution of Hydra cells in cellular aggregates . In: Physica A: Statistical Mechanics and its Applications . 293, No. 3-4, April 2001, pp. 549-558. doi : 10.1016 / S0378-4371 (01) 00009-7 .
6. ^ Matthias Weiss, Markus Elsner, Fredrik Kartberg, Tommy Nilsson: Anomalous Subdiffusion Is a Measure for Cytoplasmic Crowding in Living Cells . In: Biophysical Journal . tape 87 , no. 5 , November 2004, pp. 3518-3524 , doi : 10.1529 / biophysj.104.044263 .
7. ↑ GJ Schuetz, H. Schindler, T. Schmidt: Single-molecule microscopy on model membranes reveals anomalous diffusion . In: Biophysical Journal . 73, No. 2, August 1997, pp. 1073-1080. doi : 10.1016 / S0006-3495 (97) 78139-6 .
8. ↑ Laure Wawrezinieck, Herve Rigneault, Didier Marguet, Pierre-Francois Lenne: Fluorescence Correlation Spectroscopy Diffusion Laws to Probe the Submicron Cell Membrane Organization . In: Biophysical Journal . tape 89 , no. 6 , December 2005, p. 4029-4042 , doi : 10.1529 / biophysj.105.067959 .
9. ↑ Diego Krapf: Mechanisms Underlying Anomalous Diffusion in the Plasma Membrane . In: Current Topics in Membranes . tape 75 . Elsevier, 2015, ISBN 978-0-12-803295-4 , pp. 167–207 , doi : 10.1016 / bs.ctm.2015.03.002 ( elsevier.com [accessed November 8, 2019]).
10. ^ Shlomo Havlin, Daniel Ben-Avraham: Diffusion in disordered media . In: Advances in Physics . tape 51 , no. 1 , 2002, p. 187-292 , doi : 10.1080 / 00018730110116353 .
11. ↑ Yuval Gefen, Amnon Aharony, Shlomo Alexander: Anomalous Diffusion on Percolating Clusters . In: Physical Review Letters . 50, No. 1, January 1983, pp. 77-80. doi : 10.1103 / PhysRevLett.50.77 .
12. ^ I. Wong, M. Gardel, D. Reichman, Eric Weeks, M. Valentine, A. Bausch, D. Weitz: Anomalous Diffusion Probes Microstructure Dynamics of Entangled F-Actin Networks . In: Physical Review Letters . 92, No. 17, April 2004. doi : 10.1103 / PhysRevLett.92.178101 .
13. ^ Roman Shusterman, Sergey Alon, Tatyana Gavrinyov, Oleg Krichevsky: Monomer Dynamics in Double- and Single-Stranded DNA Polymers . In: Physical Review Letters . tape 92 , no. January 4 , 2004, doi : 10.1103 / PhysRevLett.92.048303 .
14. ↑ ^{a b} D. H. Rothman (2011): MIT lecture script "Anomalous Diffusion" ( Memento of October 10, 2015 in the Internet Archive ) (accessed on November 11, 2012; PDF; 224 kB)
15. ^ AV Weigel, B. Simon, MM Tamkun, D. Krapf: Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking . In: Proceedings of the National Academy of Sciences . tape 108 , no. 16 , April 19, 2011, ISSN  0027-8424 , p. 6438–6443 , doi : 10.1073 / pnas.1016325108 , PMID 21464280 ( pnas.org [accessed November 8, 2019]).
16. ^ ^{A b c} Christian C. Fritsch, Jörg Langowski: Kinetic lattice Monte Carlo simulation of viscoelastic subdiffusion. In: aip.scitation.org. Retrieved January 29, 2019 . 
17. ↑ Ralf Metzler, Eli Barkai, Joseph Klafter: Anomalous Diffusion and Relaxation Close to Thermal Equilibrium: A Fractional Fokker-Planck Equation Approach . In: Physical Review Letters . 82, No. 18, May 1999, pp. 3563-3567. doi : 10.1103 / PhysRevLett.82.3563 .
18. ↑ Eli Barkai: CTRW pathways to the fractional diffusion equation . In: Chemical Physics . 284, No. 1-2, November 2002, pp. 13-27. doi : 10.1016 / S0301-0104 (02) 00533-5 .