Mean square displacement

Mean square displacement of a tracer particle in a purely viscous or viscoelastic liquid

Representation of some trajectories and the resulting MSD (in the usual log-log representation) of a simple random movement. The black circles have the radius for selected  τ ${\displaystyle {\sqrt {\langle r^{2}(\tau )\rangle }}}$

The mean square displacement ( English displacement mean squared  MSD) is in the statistical physics (. B. many attempts z) travels a measure of the distance that a particle in the medium in a certain time. This measure is particularly important when describing Brownian dynamics and other random movements , since there is typically no specific direction along which a distance traveled could be measured. ${\displaystyle \langle r^{2}(\tau )\rangle }$

Clear description and interpretation

The mean square displacement is a measure of the volume that a particle that is moving randomly roams through in a certain time.

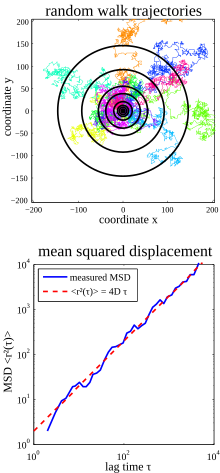
As an example, consider a pure Brownian movement in two dimensions (see figure on the right). If several particles (in the upper part of the figure in different colors) start at the same place, individual particles will move away from the starting point, but in different directions. Each particle can also return to the starting point. If one now averages over all particle positions after a waiting time τ, this average value will again be close to the starting point, i.e. the particles have not moved on average. In contrast, if the particles had a preferred direction, their mean value would also move in this preferred direction with a certain speed.

One observes, however, that the particles cover a larger area the longer one waits (concentric circles in the figure, the outer circles correspond to longer waiting times τ), i. H. the longer you wait, the sooner there is a particle at a greater distance from the starting point. The mean square displacement of all particles can be used to describe this swept area (which grows slowly with the waiting time τ): Its root describes the radius of these increasing circles / area. ${\displaystyle {\sqrt {\langle r^{2}(\tau )\rangle }}}$

The curve can therefore be interpreted in such a way that particles moving after it, after a time τ, were with high probability already to be found at a distance from their starting point. ${\displaystyle \langle r^{2}(\tau )\rangle }$ ${\displaystyle {\sqrt {\langle r^{2}(\tau )\rangle }}}$

Exact definition

The mean quadratic displacement is defined using the ensemble mean over many trajectories : ${\displaystyle {\vec {R}}_{n}(t),n=1\dotsc N}$

${\displaystyle \langle r^{2}(\tau )\rangle =\lim \limits _{N\rightarrow \infty }{\frac {1}{N}}\cdot \sum \limits _{n=1}^{N}\left({\vec {R}}_{n}(\tau )-{\vec {R}}_{n}(0)\right)^{2}}$

Here, averaging is made over many particles, each of which is observed over the period of time . Alternatively (and above all in theoretical considerations in which these quantities can be calculated) this can also be written using the probability of being present (see Greens function ) of particles at the time : ${\displaystyle \tau }$ ${\displaystyle n({\vec {r}},\tau )}$ ${\displaystyle \tau }$

${\displaystyle \langle r^{2}(\tau )\rangle =\iiint \limits _{\mathbb {R} _{+}^{3}}r^{2}\cdot n({\vec {r}},\tau )\;\mathrm {d} ^{3}r}$

Note that measures the distance to the starting point of the trajectory (which is placed in the origin). ${\displaystyle n({\vec {r}},\tau )}$

Depending on the system, the mean quadratic displacement can also be defined using a time average over a trajectory of a particle in space: ${\displaystyle {\vec {R}}(t)}$

${\displaystyle \mathrm {MSD} (\tau )\equiv \langle r^{2}(\tau )\rangle :=\lim \limits _{T\rightarrow \infty }{\frac {1}{T}}\cdot \int \limits _{0}^{T}\left({\vec {R}}(t+\tau )-{\vec {R}}(t)\right)^{2}\;\mathrm {d} t}$

This means that only one particle is observed and, based on different points in time, it is measured how far the particle has moved up to that point. The shifts during all possible time periods within the duration of the trajectory are then averaged . ${\displaystyle t}$ ${\displaystyle t+\tau }$ ${\displaystyle \left({\vec {R}}(t+\tau )-{\vec {R}}(t)\right)^{2}}$ ${\displaystyle \tau }$ ${\displaystyle T}$

Both definitions only result in the same size if the system under consideration is ergodic (see also ergodic hypothesis ). Mixed forms of these two ideal definitions are often used, especially when both mean values ​​are mixed in experiments (e.g. in fluorescence correlation spectroscopy ).

In addition, the square root of the mean square displacement is often also used

${\displaystyle \mathrm {RMSD} (\tau ):={\sqrt {\langle r^{2}(\tau )\rangle }}}$

and then usually referred to as English root mean squared displacement (RMSD).

meaning

MSD curves for different types of movement

Particularly in the case of undirected and random movements, there is often no specific spatial direction. The averaging over the (vectorial) displacements around the starting point is therefore zero, since for every movement in one direction there is a movement in the opposite direction with the same statistical frequency. For example, the mean displacement of a random walk of a single particle is zero for all times . Nevertheless, the particle covers a certain area of ​​space in a given time, which is characterized by the mean square displacement. ${\displaystyle \langle {\vec {R}}(\tau )-{\vec {R}}(0)\rangle }$ ${\displaystyle \tau }$

For normal diffusion there is a simple relationship for the mean quadratic displacement:

${\displaystyle \langle r^{2}(\tau )\rangle =2n\cdot D\cdot \tau \ \ \ \ \ \ \ \ \ \mathrm {\mathbf {(*)} } }$

With

• ${\displaystyle D}$the diffusion coefficient
• ${\displaystyle n}$the number of spatial dimensions in which the movement takes place.

For normal diffusion in connection with a directed movement (flow of velocity ) the following results: ${\displaystyle V}$

${\displaystyle \langle r^{2}(\tau )\rangle =2n\cdot D\cdot \tau +(V\cdot \tau )^{2}}$

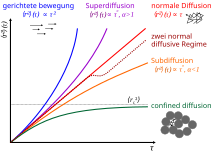
In the case of anomalous diffusion , the connection is often more general:

${\displaystyle \langle r^{2}(\tau )\rangle =2n\cdot \Gamma _{\alpha }\cdot \tau ^{\alpha }}$

With

• the generalized diffusion coefficient , a proportionality constant that u. U. depends on ${\displaystyle \Gamma _{\alpha }}$ ${\displaystyle \alpha }$
• ${\displaystyle \alpha }$ to describe the anomaly of movement:
  • for one speaks of subdiffusion , ${\displaystyle \alpha <1}$
  • for of superdiffusion , ${\displaystyle \alpha >1}$
  • for , normal diffusion again results. ${\displaystyle \alpha =1}$

Diffusion often takes place in porous media , with only a fraction of the total volume being accessible to the particles. In such systems one often sees a transition between two normal-diffusive regimes: First, rapid diffusion occurs within a pore . On longer time scales, the MSD then changes to a slower, but still normally diffusive regime that describes the diffusion between the pores.

If the proportion of the inaccessible volume is so large that the pores are no longer necessarily connected, the particles are trapped in the resulting delimited spatial areas. One speaks of confined diffusion . For large time scales , the MSD then moves towards a constant value that describes the size of the accessible area. The MSD can then be modeled as follows (with free fit parameters ): ${\displaystyle \langle r_{\text{c}}\rangle }$ ${\displaystyle A_{1},A_{2}}$

${\displaystyle \langle r^{2}(\tau )\rangle =\langle r_{\text{c}}\rangle ^{2}\cdot \left(1-A_{1}\cdot \exp \left[-A_{2}\cdot {\frac {2n\cdot D\tau }{\langle r_{\text{c}}\rangle ^{2}}}\right]\right)}$

In many systems the anomaly of a movement is limited to a certain time range for . Above this critical time , the movement returns to normal diffusion. This case is e.g. B. can be seen in the curve for viscoelastic liquids and occurs z. B. also on the monomer dynamics of polymers (see Rouse model ). ${\displaystyle \tau _{c}}$ ${\displaystyle \tau _{c}}$

Measurement and application

The mean quadratic displacement is often used to characterize random movements in simulations. It can be determined directly from the simulated particle trajectories. With the help of the  (*) relationship (see above) for normal diffusion, a diffusion coefficient  D can be defined based on the grid width  a and the time step  Δt of the simulation:

${\displaystyle D:={\frac {a^{2}}{2n\cdot \Delta t}}}$

The simulation, which often runs in idealized and normalized coordinates, can then be normalized to real systems.

The mean square displacement is also accessible experimentally. For example, it can be determined directly from the trajectories measured there using single-particle tracking techniques. It is also experimentally accessible with the help of fluorescence correlation spectroscopy under certain assumptions. The diffusion coefficient can then also be determined from the measured curve derr² (τ)⟩:

${\displaystyle D={\frac {1}{2n}}\cdot \lim \limits _{\tau \rightarrow \infty }{\frac {\mathrm {d} }{\mathrm {d} \tau }}\langle r^{2}(\tau )\rangle }$

Connection to speed autocorrelation

The mean square displacement is closely related to the speed autocorrelation function via the Green-Kubo relation : ${\displaystyle \langle {\vec {v}}(t)\cdot {\vec {v}}(t+\tau )\rangle }$

${\displaystyle \langle {\vec {v}}(t)\cdot {\vec {v}}(t+\tau )\rangle =-{\frac {\mathrm {d} }{\mathrm {d} \tau }}{\frac {\langle r^{2}(\tau )\rangle }{6\tau }}}$

Web links

• NSDL Materials Digital Library Wiki: softmatter: Mean Squared Displacement ( Memento February 25, 2012 in the Internet Archive ), accessed August 5, 2012

Individual evidence

1. ↑ ^{a b} Vincent Tejedor, Olivier Benichou, Raphael Voituriez, Ralf Jungmann, Friedrich Simmel, Christine Selhuber-Unkel, Lene B. Oddershede, Ralf Metzler: Quantitative Analysis of Single Particle Trajectories: Mean Maximal Excursion Method . In: Biophysical Journal . tape 98 , no. 7 , April 2010, ISSN  0006-3495 , p. 1364–1372 , doi : 10.1016 / j.bpj.2009.12.4282 .
2. ↑ ^{a b} Ralf Metzler, Joseph Klafter: The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics . In: Journal of Physics A: Mathematical and General . tape 37 , no. 31 , August 6, 2004, ISSN  0305-4470 , p. R161 – R208 , doi : 10.1088 / 0305-4470 / 37/31 / R01 ( PDF ).
3. ↑ VV Loskutov, VA Sevriugin: A novel approach to interpretation of the time-dependent self-diffusion coefficient as a sample of porous media geometry . In: Journal of Magnetic Resonance . tape 230 , May 2013, p. 1 , doi : 10.1016 / j.jmr.2013.01.004 .
4. ↑ Michael Baum, Fabian Erdel, Malte Wachsmuth, Karsten Rippe: Retrieving the intracellular topology from multi-scale protein mobility mapping in living cells . In: Nature Communications . tape 5 , July 24, 2014, doi : 10.1038 / ncomms5494 .
5. ↑ A. Kusumi, Y. Sako, M. Yamamoto: Confined lateral diffusion of membrane receptors as studied by single particle tracking (nanovid microscopy). Effects of calcium-induced differentiation incultured epithelial cells . In: Biophysical Journal . tape 65 , no. 5 , November 1993, pp. 2021 , doi : 10.1016 / S0006-3495 (93) 81253-0 .
6. ^ Michael J. Saxton, Ken Jacobson: SINGLE-PARTICLE TRACKING: Applications to Membrane Dynamics . In: Annual Review of Biophysics and Biomolecular Structure . tape 26 , no. 1 , June 1997, ISSN  1056-8700 , p. 373–399 , doi : 10.1146 / annurev.biophys.26.1.373 ( PDF ( Memento from April 23, 2014 in the Internet Archive )).
7. ↑ Sripad Ram, Prashant Prabhat, Jerry Chao, E. .. Sally Ward, Raimund J. Ober: High Accuracy 3D Quantum Dot Tracking with Multifocal Plane Microscopy for the Study of Fast Intracellular Dynamics in Live Cells . In: Biophysical Journal . tape 95 , no. December 12 , 2008, ISSN  0006-3495 , p. 6025-6043 , doi : 10.1529 / biophysj.108.140392 .
8. ^ Roman Shusterman, Sergey Alon, Tatyana Gavrinyov, Oleg Krichevsky: Monomer Dynamics in Double- and Single-Stranded DNA Polymers . In: Physical Review Letters . tape 92 , no. January 4 , 2004, ISSN  0031-9007 , doi : 10.1103 / PhysRevLett.92.048303 .
9. ^ Robert Zwanzig: Nonequilibrium Statistical Mechanics Oxford University Press, USA, 2001, ISBN 978-0-19-514018-7
10. ^ John H. van Zanten, Samiul Amin, Ahmed A. Abdala: Brownian Motion of Colloidal Spheres in Aqueous PEO Solutions . In: Macromolecules . tape 37 , no. May 10 , 2004, ISSN  0024-9297 , p. 3874-3880 , doi : 10.1021 / ma035250p .