Generalized binomial distribution

Generalized binomial distribution
Probability distribution
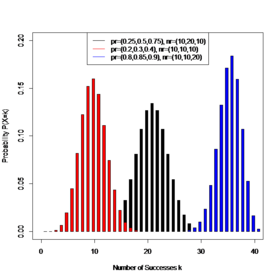
Distribution function
parameter	${\displaystyle \mathbf {p} \in [0,1]^{n}}$- Probability of success for each of the n attempts
carrier	${\displaystyle k\in \{0,\dots ,n\}}$
Density function	${\displaystyle \sum \limits _{A\in B_{k}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}(1-p_{j})}$
Distribution function	${\displaystyle \sum \limits _{l=0}^{k}\sum \limits _{A\in B_{l}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}{(1-p_{j})}}$
Expected value	${\displaystyle \sum \limits _{i=1}^{n}p_{i}}$
Variance	${\displaystyle \sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}}}$
Crookedness	${\displaystyle {\frac {\sum \limits _{i=1}^{n}{\left(1-2{p_{i}}\right)\left(1-{{p}_{i}}\right){{p}_{i}}}}{(\sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}})^{\frac {3}{2}}}}}$
Bulge	${\displaystyle 3+{\frac {\sum \limits _{i=1}^{n}{\left(1-6(1-p_{i}){p_{i}}\right)\left(1-p_{i}\right)p_{i}}}{(\sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}})^{4}}}}$
Moment generating function	${\displaystyle \prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{t}})}$
Characteristic function	${\displaystyle \prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{it}})}$

The generalized binomial distribution (sometimes also called Poisson's generalization of the binomial distribution , or Poisson binomial distribution ) is a probability distribution and can therefore be assigned to the mathematical sub-area of stochastics . It is a univariate discrete probability distribution . It is defined as the sum of independent , not necessarily identically distributed random variables that are subject to a Bernoulli distribution .

The generalized binomial distribution describes the success of a series of independent experiments, which can each assume exactly two results. The difference to the binomial distribution is that each attempt can be assigned a different probability of success.

It is also possible to define the generalized binomial distribution as the sum of independent, non-identical, binomially distributed random variables, whereby the Bernoulli random variables with identical success probabilities are combined to binomially distributed random variables.

Definition of the generalized binomial distribution

A discrete random variable follows a Generalized binomial distribution with parameter vector when the following probability function has ${\displaystyle X}$ ${\displaystyle p}$

${\displaystyle \rho _{X}(k)=\sum \limits _{A\in B_{k}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}(1-p_{j})}$,

where denotes the vector of the probabilities of success per attempt and the total number of successes in attempts . ${\displaystyle p=(p_{1},\dots ,p_{n})}$ ${\displaystyle k}$ ${\displaystyle n}$

Notation: ${\displaystyle X\sim GB(p)}$

${\displaystyle B_{k}}$is the set of all -elementary subsets that can be formed from the carrier . is the complement of , that is . ${\displaystyle k}$ ${\displaystyle \{1,2,\dots ,n\}}$ ${\displaystyle A^{c}}$ ${\displaystyle A}$ ${\displaystyle A^{c}=\{1,2,\dots ,n\}\backslash A}$

The associated distribution function is

${\displaystyle F_{X}(k)=P(X\leq k)=\sum \limits _{l=0}^{k}\sum \limits _{A\in B_{l}}\prod \limits _{i\in A}p_{i}\prod \limits _{j\in A^{c}}{(1-p_{j})}}$

Alternative parameterization

The generalized binomial distribution can also be defined as the sum of binomially distributed random variables by combining the Bernoulli random variables with the same success probabilities to binomially distributed random variables.

${\displaystyle GB(k|p)=GB(k|pr,nr)}$,

whereby the parameter vector contains the success probabilities of binomially distributed random variables and the parameter vector the respective number of attempts. ${\displaystyle pr=(pr_{1},\dots ,pr_{r})}$ ${\displaystyle r}$ ${\displaystyle nr=(nr_{1},\dots ,nr_{r})}$

It is therefore true . Here is the one vector of the length , consisting of all ones. ${\displaystyle p=(p_{1},\dots ,p_{n})=(pr_{1}\cdot 1_{nr_{1}}^{T},\dots ,pr_{r}\cdot 1_{nr_{r}}^{T})}$ ${\displaystyle 1_{nr_{i}}^{T}}$ ${\displaystyle nr_{i}}$

Properties of the generalized binomial distribution

${\displaystyle X}$in the following be a random variable that follows a generalized binomial distribution . ${\displaystyle X\sim GB(p)}$

Expected value

The generalized binomial distribution has the expectation value

${\displaystyle E(X)=\sum \limits _{i=1}^{n}p_{i}}$

Variance

The generalized binomial distribution has the variance

${\displaystyle Var(X)=\sum \limits _{i=1}^{n}(1-{p_{i}}){p_{i}}}$

Crookedness

The generalized binomial distribution is skewed

${\displaystyle v(X)={\frac {\sum \limits _{i=1}^{n}{\left(1-2{p_{i}}\right)\left(1-{{p}_{i}}\right){{p}_{i}}}}{(\sum \limits _{i=1}^{n}\left(1-{p_{i}}){p_{i}}\right)^{\frac {3}{2}}}}}$

Bulge and excess

The generalized binomial distribution has the curvature

${\displaystyle \beta _{2}=3+{\frac {\sum \limits _{i=1}^{n}{\left(1-6(1-p_{i}){p_{i}}\right)\left(1-p_{i}\right)p_{i}}}{(\sum \limits _{i=1}^{n}\left(1-{p_{i}}){p_{i}}\right)^{2}}}}$

and with it the excess

${\displaystyle \gamma =\beta _{2}-3={\frac {\sum \limits _{i=1}^{n}{\left(1-6(1-p_{i}){p_{i}}\right)\left(1-p_{i}\right)p_{i}}}{(\sum \limits _{i=1}^{n}\left(1-{p_{i}}){p_{i}}\right)^{2}}}}$

Accumulators

The cumulative generating function is

${\displaystyle g_{X}(t)=\sum _{i=1}^{n}\ln(1-p_{i}+p_{i}e^{t})}$.

Therefore, the kth cumulant is exactly the sum of the kth cumulants of the n Bernoulli-distributed random variables from which the generalized binomial distribution is composed:

${\displaystyle \tau _{k}=\tau _{k}^{1}+\dots +\tau _{k}^{n}}$

The recursion equation of the cumulants of the Bernoulli distribution then also applies to these cumulants

Probability generating function

The probability generating function of the generalized binomial distribution is

${\displaystyle m_{X}(t)=\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{t})}$

Characteristic function

The characteristic function of the generalized binomial distribution is:

${\displaystyle \varphi _{X}(t)=\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{it}})}$

Moment generating function

The moment-generating function of the generalized binomial distribution is:

${\displaystyle M_{X}(t)=\prod \limits _{j=1}^{n}(1-{p_{j}}+{p_{j}}{e^{t}})}$

Sum of generalized binomial random variables

Is and two independent generalized binomial random variables, then is generalized binomial distribution: . Hence the generalized binomial distribution is reproductive . ${\displaystyle X\sim GB_{n}(p_{1},\dots p_{n})}$ ${\displaystyle Y\sim GB_{m}(p_{1},\dots p_{m})}$ ${\displaystyle X+Y}$ ${\displaystyle X+Y\sim GB_{n+m}(p_{1},\dots p_{n+m})}$

Relationship to other distributions

Relationship to the binomial distribution

The sum of mutually independent binomially distributed random variables is generally binomially distributed. If all success probabilities are equal, that is , then the generalized binomial distribution results in the binomial distribution. In fact, the binomial distribution for fixed expectation and fixed order is the generalized binomial distribution with maximum entropy . That is, under the condition that the parameter vector of the length has maximizes the entropy . ${\displaystyle X_{i}\sim B(n_{i},p_{i})}$ ${\displaystyle p_{i}=p_{j}\;\forall i,j=1\dots ,n}$ ${\displaystyle p}$ ${\displaystyle X\sim GB(p)}$ ${\displaystyle n}$ ${\displaystyle p=(E(X)/n,\dots ,E(X)/n)}$ ${\displaystyle \mathrm {H} (X)}$

Relationship to the Bernoulli distribution

The sum of mutually independent Bernoulli-distributed random variables , which all have a different parameter , is generally binomially distributed. ${\displaystyle n}$ ${\displaystyle X_{i}}$ ${\displaystyle p_{i}}$

Approximation by the Poisson distribution

→ Main article : Poisson approximation

For a very large number of attempts and very small but different probabilities of success , the probability function of the generalized binomial distribution can be approximated by the Poisson distribution . ${\displaystyle n}$ ${\displaystyle p_{1},\dots ,p_{n}}$

${\displaystyle \rho _{X}(k)\approx {\frac {\lambda ^{k}}{k!}}\cdot \mathrm {e} ^{-\lambda }}$

The parameter is equal to the expectation value of the generalized binomial distribution . ${\displaystyle \lambda }$

Approximation by the normal distribution

The distribution function of the generalized binomial distribution can be approximated by the normal distribution for a very large number of experiments . ${\displaystyle n}$

${\displaystyle F_{X}(k)\approx \Phi \left({\frac {k+0{,}5-\mu }{\sigma }}\right),\ k=0,\dots ,n}$

The parameter corresponds to the expected value and the standard deviation of the generalized binomial distribution . is the distribution function of the standard normal distribution . ${\displaystyle \mu }$ ${\displaystyle \sigma }$ ${\displaystyle \Phi (\cdot )}$

Examples

Radar control

An employee must drive to work on the motorway and through the local area every working day. The probabilities of getting into a radar control are on the motorway and in the local area. ${\displaystyle 0{,}5\,\%}$ ${\displaystyle 1\,\%}$

How high are the chances of getting into controls on a working day ? ${\displaystyle 0,1,2}$

The random number of radar controls can be modeled as the sum of two Bernoulli-distributed random variables for the motorway and for the local area:, with ${\displaystyle R}$ ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$ ${\displaystyle R=R_{1}+R_{2}}$

${\displaystyle R_{1}={\begin{cases}1,&{\text{Kontrolle mit Wahrscheinlichkeit }}0{,}005\\0,&{\text{keine Kontrolle mit Wahrscheinlichkeit }}0{,}995\end{cases}}}$

${\displaystyle R_{2}={\begin{cases}1,&{\text{Kontrolle mit Wahrscheinlichkeit }}0{,}01\\0,&{\text{keine Kontrolle mit Wahrscheinlichkeit }}0{,}99\end{cases}}}$

Since and have different probabilities of success, this example cannot be solved using the binomial distribution. ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$

${\displaystyle R}$follows a generalized binomial distribution with a parameter vector . ${\displaystyle p=(0{,}005,0{,}01)}$

The probabilities we are looking for can be calculated as follows:

• ${\displaystyle 0}$ Controls: ${\displaystyle P(R=0)}$

${\displaystyle P(R=0)=P(R_{1}=0)\cdot P(R_{2}=0)=0{,}995\cdot 0{,}99=0{,}98505=98{,}505\,\%}$

• ${\displaystyle 1}$ Control: ${\displaystyle P(R=1)}$

${\displaystyle P(R=1)=P(R_{1}=1)\cdot P(R_{2}=0)+P(R_{1}=0)\cdot P(R_{2}=1)=0{,}005\cdot 0{,}99+0{,}995\cdot 0{,}01=0{,}0149=1{,}49\,\%}$

• ${\displaystyle 2}$ Controls: ${\displaystyle P(R=2)}$

${\displaystyle P(R=2)=P(R_{1}=1)\cdot P(R_{2}=1)=0{,}005\cdot 0{,}01=0{,}00005=0{,}005\,\%}$

Manufacturing process

Devices are produced in a factory and then subjected to quality control. It can different types of faults. The probabilities that a particular error type will occur are for the error of the type and for the error types and, respectively . ${\displaystyle 3}$ ${\displaystyle 4\,\%}$ ${\displaystyle 1}$ ${\displaystyle 7\,\%}$ ${\displaystyle 2}$ ${\displaystyle 3}$

What are the chances that a device will be produced with errors? ${\displaystyle 0,1,2,3}$

The random number of errors can be written as the sum of three Bernoulli-distributed random variables , and :, with ${\displaystyle F}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle F_{3}}$ ${\displaystyle F=F_{1}+F_{2}+F_{3}}$

${\displaystyle F_{1}={\begin{cases}1,&{\text{Fehler mit Wahrscheinlichkeit }}0{,}04\\0,&{\text{kein Fehler mit Wahrscheinlichkeit }}0{,}96\end{cases}}}$

${\displaystyle F_{2}=F_{3}={\begin{cases}1,&{\text{Fehler mit Wahrscheinlichkeit }}0{,}07\\0,&{\text{kein Fehler mit Wahrscheinlichkeit }}0{,}93\end{cases}}}$

${\displaystyle F}$has a generalized binomial distribution with a parameter vector . ${\displaystyle p=(0{,}04,0{,}07,0{,}07)}$

Alternatively, the parameterization can be selected by combining the identical Bernoulli random variables into a binomially distributed random variable. ${\displaystyle pr=(0{,}04,0{,}07),\ nr=(1,2)}$

The probabilities we are looking for can be calculated as follows:

• ${\displaystyle 0}$ Error: ${\displaystyle P(F=0)}$

${\displaystyle P(F=0)=P(F_{1}=0)\cdot P(F_{2}=0)\cdot P(F_{3}=0)=0{,}96\cdot 0{,}93\cdot 0{,}93=0{,}830304=83{,}0304\,\%}$

• ${\displaystyle 1}$ Error: ${\displaystyle P(F=1)}$

${\displaystyle {\begin{aligned}P(F=1)&=P(F_{1}=1)\cdot P(F_{2}=0)\cdot P(F_{3}=0)+P(F_{1}=0)\cdot P(F_{2}=1)\cdot P(F_{3}=0)+P(F_{1}=0)\cdot P(F_{2}=0)\cdot P(F_{3}=1)\\&=0{,}04\cdot 0{,}93\cdot 0{,}93+0{,}96\cdot 0{,}07\cdot 0{,}93+0{,}96\cdot 0{,}93\cdot 0{,}07=0{,}159588=15{,}9588\,\%\end{aligned}}}$

• ${\displaystyle 2}$ Error: ${\displaystyle P(F=2)}$

${\displaystyle {\begin{aligned}P(F=2)&=P(F_{1}=1)\cdot P(F_{2}=1)\cdot P(F_{3}=0)+P(F_{1}=0)\cdot P(F_{2}=1)\cdot P(F_{3}=1)+P(F_{1}=1)\cdot P(F_{2}=0)\cdot P(F_{3}=1)\\&=0{,}04\cdot 0{,}07\cdot 0{,}93+0{,}96\cdot 0{,}07\cdot 0{,}07+0{,}04\cdot 0{,}93\cdot 0{,}07=0{,}009912=0{,}9912\,\%\end{aligned}}}$

• ${\displaystyle 3}$ Error: ${\displaystyle P(F=3)}$

${\displaystyle P(F=3)=P(F_{1}=1)\cdot P(F_{2}=1)\cdot P(F_{3}=1)=0{,}04\cdot 0{,}07\cdot 0{,}07=0{,}000196=0{,}0196\,\%}$

Application & calculation

The generalized binomial distribution is used in many areas; z. B. surveys, manufacturing processes, quality assurance. However, an approximation is often used because the exact calculation is very complex. Without the appropriate software, even simple models with a few Bernoulli random variables can hardly be calculated.

Random numbers

The inversion method can be used to generate random numbers . Alternatively, you can also generate Bernoulli-distributed random numbers for the parameters and add them up. The result is then generalized binomially distributed. ${\displaystyle n}$ ${\displaystyle p_{i}}$

literature

• M.Fisz, probability calculation and mathematical statistics, VEB Deutscher Verlag der Wissenschaften, 1973, p. 164 ff.
• KJ Klauer, Criterion-Oriented Tests, Verlag für Psychologie, Hogrefe, 1987, Göttingen, p. 208 ff.

Web links

• GenBinomApps - R Package . R Package for the computation of Clopper Pearson confidence intervals and the generalized binomial distribution. Retrieved July 30, 2015.

Individual evidence

1. ^ On the Number of Successes in Independent Trials . (PDF; 1.6 MB) YHWang, Statistica Sinica, Vol. 3, 1993, p. 295-312. Retrieved September 23, 2013.
2. ↑ ^{a b c} On Computing the Distribution Function for the Sum of Independent and Non-identical Random Indicators . ( Memento of the original from October 23, 2015 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF; 110 kB) Y. Hong, Blacksburg, USA, April 5, 2011. Retrieved September 23, 2013. 
3. ↑ Peter Harremoës: Binomial and Poisson Distributions as Maximum Entropy Distributions . In: IEEE Information Theory Society (Ed.): IEEE Transactions on Information Theory . 47, 2001, pp. 2039-2041. doi : 10.1109 / 18.930936 .