Poisson approximation

Comparison of the Poisson distribution (black lines) and the binomial distribution with (red circles), (blue circles), (green circles). All distributions have an expected value of 5. The horizontal axis shows the number of events that have occurred . The larger it gets, the better the approximation of the binomial distribution by the Poisson distribution. ${\displaystyle n=10}$ ${\displaystyle n=20}$ ${\displaystyle n=1000}$ ${\displaystyle k}$ ${\displaystyle n}$

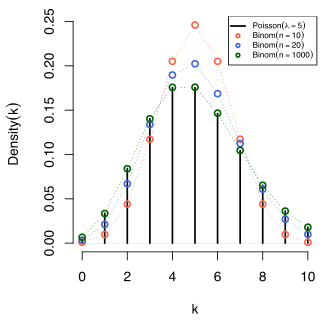
The Poisson approximation is in the probability theory one way the binomial distribution and the generalized binomial distribution for large samples and small probabilities by the Poisson distribution to approximate. By crossing the limit to infinity one then obtains the convergence in the distribution of the two binomial distributions against the Poisson distribution.

formulation

If is a sequence of binomially distributed random variables with parameters and , so that for the expected values for , then follows ${\displaystyle (S_{n})}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle p_{n}}$ ${\displaystyle E(S_{n})=n\cdot p_{n}\to \lambda >0}$ ${\displaystyle n\to \infty }$

${\displaystyle P(S_{n}=k)=B_{n,p_{n}}(\{k\})\to \,{\frac {\lambda ^{k}}{k!}}\mathrm {e} ^{-\lambda }=P_{\lambda }(\{k\})\quad }$

for . ${\displaystyle n\to \infty }$

Proof sketch

The value of a Poisson-distributed random variable at this point is the limit value of a binomial distribution with at the point : ${\displaystyle k}$ ${\displaystyle n\to \infty }$ ${\displaystyle p={\tfrac {\lambda }{n}}}$ ${\displaystyle k}$

${\displaystyle {\begin{aligned}\lim _{n\to \infty }P(S_{n}=k)&=\lim _{n\to \infty }{\frac {n!}{k!\,(n-k)!}}\left({\frac {\lambda }{n}}\right)^{k}\left(1-{\frac {\lambda }{n}}\right)^{n-k}\\&=\lim _{n\to \infty }\left({\frac {\lambda ^{k}}{k!}}\right)\left({\frac {n(n-1)(n-2)\cdots (n-k+1)}{n^{k}}}\right)\left(1-{\frac {\lambda }{n}}\right)^{n}\left(1-{\frac {\lambda }{n}}\right)^{-k}\\&={\frac {\lambda ^{k}}{k!}}\cdot \lim _{n\to \infty }\underbrace {\left({\frac {n}{n}}\cdot {\frac {n-1}{n}}\cdot {\frac {n-2}{n}}\cdots {\frac {n-k+1}{n}}\right)} _{\to 1}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to e^{-\lambda }}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\\&={\frac {\lambda ^{k}\mathrm {e} ^{-\lambda }}{k!}}.\end{aligned}}}$

With large and small samples, the binomial distribution can consequently be approximated well using the Poisson distribution. ${\displaystyle p}$

The representation as the limit value of the binomial distribution allows an alternative calculation of the expected value and variance of the Poisson distribution. Let be independent Bernoulli distributed random variables with and be . For true and ${\displaystyle X_{1},\dotsc ,X_{n}\,n}$ ${\displaystyle \,p=\lambda /n}$ ${\displaystyle S_{n}:=X_{1}+\dotsb +X_{n}}$ ${\displaystyle n\to \infty }$ ${\displaystyle S_{n}\sim P_{\lambda }}$

${\displaystyle {\begin{aligned}\operatorname {E} (S_{n})&=\operatorname {E} (X_{1})+\dotsb +\operatorname {E} (X_{n})=\underbrace {{\frac {\lambda }{n}}+\dotsb +{\frac {\lambda }{n}}} _{n\,\mathrm {mal} }=\lambda \to \lambda \\\operatorname {Var} (S_{n})&=\operatorname {Var} (X_{1})+\dotsb +\operatorname {Var} (X_{n})\\&=\underbrace {{\frac {\lambda }{n}}\left(1-{\frac {\lambda }{n}}\right)+\dotsb +{\frac {\lambda }{n}}\left(1-{\frac {\lambda }{n}}\right)} _{n\,\mathrm {mal} }=\lambda \left(1-{\frac {\lambda }{n}}\right)\to \lambda .\end{aligned}}}$

Goodness of the approximation

The following applies to the error estimation

${\displaystyle \sum _{k\geq 0}\left|B_{n,p}(\{k\})-P_{n\cdot p}(\{k\})\right|\leq 2np^{2}}$.

The approximation of a sum of Bernoulli-distributed random variables (or a binomial-distributed random variable) is therefore particularly good for small ones. As a rule of thumb, the approximation is good if and holds. If , the normal approximation is more suitable. ${\displaystyle p}$ ${\displaystyle n\geq 50}$ ${\displaystyle p\leq 0{,}05}$ ${\displaystyle p\approx 0{,}5}$

generalization

More generally, the following can be shown: Are stochastically independent random variables with (each random variable is thus Bernoulli-distributed ). Then ${\displaystyle X_{1},\dotsc ,X_{n}}$ ${\displaystyle P(X_{i}=1)=p_{i}=1-P(X_{i}=0)}$

${\displaystyle S:=\sum _{i=1}^{n}X_{i}}$

generalized binomially and it is

${\displaystyle \lambda =\sum _{i=1}^{n}p_{i}}$.

Then applies

${\displaystyle \sum _{k=0}^{\infty }\left|P(S=k)-\exp(-\lambda ){\frac {\lambda ^{k}}{k!}}\right|\leq 2\sum _{i=1}^{n}p_{i}^{2}}$.

Applies to all , then is binomially distributed and the above result follows immediately. ${\displaystyle p_{i}=p_{j}}$ ${\displaystyle 1\leq i,j\leq n}$ ${\displaystyle S}$

example

An individual of a species produces offspring that all stochastically independently of one another have a probability of reaching sexual maturity. One is now interested in the probability that two or more offspring will reach sexually mature age. ${\displaystyle n=1000}$ ${\displaystyle p_{i}=0{,}001}$

Exact solution

Let the random variable “The -th descendant reach sexually mature age”. It applies and for all . Then the number of surviving offspring is -distributed due to stochastic independence . For modeling, one defines the probability space with the result set , the number of surviving sexually mature offspring. The σ-algebra is canonically then the power set of the result set: and as a probability distribution, the binomial distribution : . Is wanted . There is therefore a probability of approx. 26% that at least two individuals will reach sexually mature age. ${\displaystyle X_{i}=1}$ ${\displaystyle i}$ ${\displaystyle P(X_{i}=1)=p_{i}}$ ${\displaystyle P(X_{i}=0)=1-p_{i}}$ ${\displaystyle i}$ ${\displaystyle S:=\sum _{i=1}^{n}X_{i}}$ ${\displaystyle B_{n,p}}$ ${\displaystyle (\Omega ,\Sigma ,P)}$ ${\displaystyle \Omega :=\{0,\dotsc ,n\}}$ ${\displaystyle \Sigma :={\mathcal {P}}(\Omega )}$ ${\displaystyle P(\{k\}):=B_{n,p}(\{k\})}$ ${\displaystyle P(S\geq 2)=1-P(S=1)-P(S=0)=1-B_{1000;\,0{,}001}(\{0\})-B_{1000;\,0{,}001}(\{1\})\approx 0{,}2642}$

Approximate solution

Since is sufficiently large and sufficiently small, the binomial distribution can be approximated with sufficient accuracy using the Poisson distribution. This time the probability space is defined by means of the result space , the algebra and the Poisson distribution as the probability distribution with the parameter . It should be noted here that the two modeled probability spaces are different, since the Poisson distribution does not define a probability distribution on a finite result space. So the likelihood that at least two individuals will reach sexually mature age is . ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle (\Omega ,\Sigma ,P)}$ ${\displaystyle \Omega :=\mathbb {N} }$ ${\displaystyle \sigma }$ ${\displaystyle \Sigma :={\mathcal {P}}(\mathbb {N} )}$ ${\displaystyle P(\{k\}):=P_{\lambda }(\{k\})={\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }}$ ${\displaystyle \lambda =n\cdot p=1}$ ${\displaystyle P(S\geq 2)\approx 1-P_{\lambda }(\{1\})-P_{\lambda }(\{0\})=1-{\frac {\lambda ^{1}}{1!}}e^{-1}-{\frac {\lambda ^{0}}{0!}}e^{-1}\approx 0{,}2642}$

With the exception of four decimal places, the exact solution corresponds to the Poisson approximation.

Web links

• AV Prokhorov: Poisson's theorem . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).

• Eric W. Weisstein : Poisson theorem . In: MathWorld (English).

literature

• Achim Klenke: Probability Theory . 3. Edition. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6 , doi : 10.1007 / 978-3-642-36018-3 .
• Ulrich Krengel: Introduction to probability theory and statistics . For studies, professional practice and teaching. 8th edition. Vieweg, Wiesbaden 2005, ISBN 3-8348-0063-5 , doi : 10.1007 / 978-3-663-09885-0 .
• Hans-Otto Georgii: Stochastics . Introduction to probability theory and statistics. 4th edition. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , doi : 10.1515 / 9783110215274 .