Chi-square test
In mathematical statistics, a chi-square test ( test ) denotes a group of hypothesis tests with a chi-square-distributed test test variable .
A distinction is mainly made between the following tests:
- Distribution test (also fit test given): Here, it is checked whether data present in a particular manner distributed are.
- Independence test: Here it is checked whether two features are stochastically independent .
- Homogeneity test: Here it is checked whether two or more samples come from the same distribution or a homogeneous population.
The chi-square test and its test statistic were first described by Karl Pearson in 1900 .
Distribution test
We are looking at a statistical characteristic whose probabilities are unknown in the population. With regard to the probabilities of, it becomes a provisionally generally formulated null hypothesis
- : The characteristic has the probability distribution
set up.
method
There are independent observations of the trait that fall into different categories. If a characteristic has a large number of characteristics, it is expedient to group them together in classes and see the classes as categories. The number of observations in the -th category is the observed frequency .
One now thinks about how many observations on average would have to lie in a category if the hypothetical distribution actually had. To do this, one first calculates the probability that a characteristic of falls into the category . The absolute frequency to be expected below is:
If the frequencies observed in the present sample deviate “too much” from the expected frequencies, the null hypothesis is rejected. The test variable for the test
measures the size of the deviation.
If the test variable is sufficiently large, it is approximately chi-square distributed with degrees of freedom . If the null hypothesis is true, the difference between the observed frequency and the theoretically expected frequency should be small. So if the test variable value is high, it is rejected. The denial area for is on the right.
At a level of significance is rejected if true when the so obtained from the sample value of the test statistic is larger than the - quantile of the distribution with 's degrees of freedom.
There are tables of the quantiles ( critical values ) depending on the number of degrees of freedom and the desired level of significance ( see below ).
If the significance level that belongs to a certain value is to be determined, an intermediate value must usually be calculated from the table. Logarithmic interpolation is used for this .
particularities
Estimation of distribution parameters
In general, one specifies the parameters of the distribution in the distribution hypothesis. If these cannot be specified, they must be estimated from the sample. With the chi-square distribution, one degree of freedom is lost for each estimated parameter. It therefore has degrees of freedom with the number of estimated parameters. For the normal distribution it would be if the expected value and the variance are estimated.
Minimum size of the expected frequencies
So that the test variable can be viewed as approximately chi-square distributed, each expected frequency must have a certain minimum size. Various textbooks put this at 1 or 5. If the expected frequency is too small, several classes can possibly be combined in order to achieve the minimum size.
Example of the distribution test
The sales of approx. 200 listed companies are available. The following histogram shows their distribution.
Let it be the turnover of a company [million €].
We now want to test the hypothesis that is normally distributed .
Since the data are available in many different forms, they have been divided into classes. The table resulted:
| class | interval | Observed frequency | |
| j | over | to | n y |
| 1 | ... | 0 | 0 |
| 2 | 0 | 5000 | 148 |
| 3 | 5000 | 10,000 | 17th |
| 4th | 10,000 | 15000 | 5 |
| 5 | 15000 | 20000 | 8th |
| 6th | 20000 | 25,000 | 4th |
| 7th | 25,000 | 30000 | 3 |
| 8th | 30000 | 35000 | 3 |
| 9 | 35000 | ... | 9 |
| total | 197 | ||
Since no parameters are specified, they are determined from the sample. It's appreciated
and
It is tested:
- : is normally distributed with the expected value and the standard deviation .
In order to determine the frequencies below expected, the probabilities that fall into the given classes are first calculated . One then calculates
It contains a random variable with a standard normal distribution and its distribution function. Analogously one calculates:
-
- ...
This gives the expected frequencies
- ...
For example, around 25 companies would have to have an average turnover between 0 € and 5000 € if the characteristic turnover is actually normally distributed.
The expected frequencies, along with the observed frequencies, are listed in the following table.
| class | interval | Observed frequency | probability | Expected frequency | |
| j | over | to | n y | p 0j | n 0y |
| 1 | ... | 0 | 0 | 0.3228 | 63.59 |
| 2 | 0 | 5000 | 148 | 0.1270 | 25.02 |
| 3 | 5000 | 10,000 | 17th | 0.1324 | 26.08 |
| 4th | 10,000 | 15000 | 5 | 0.1236 | 24.35 |
| 5 | 15000 | 20000 | 8th | 0.1034 | 20.36 |
| 6th | 20000 | 25,000 | 4th | 0.0774 | 15.25 |
| 7th | 25,000 | 30000 | 3 | 0.0519 | 10.23 |
| 8th | 30000 | 35000 | 3 | 0.0312 | 6.14 |
| 9 | 35000 | ... | 9 | 0.0303 | 5.98 |
| total | 197 | 1.0000 | 197.00 | ||
The test variable is now determined as follows:
At a significance level , the critical value lies Testprüfgröße at . There , the null hypothesis is rejected. It can be assumed that the sales characteristic is not normally distributed in the population.
complement
The above data were then logarithmized . Based on the result of the test of the data set of the logarithmized data for normal distribution, the null hypothesis of normal distribution of the data could not be rejected at a significance level of 0.05. Provided that the logarithmized sales data actually come from a normal distribution, the original sales data are logarithmically normalized .
The following histogram shows the distribution of the logarithmized data.
Chi-square distribution test in jurisdiction
In Germany, the chi-square distribution test was judicially confirmed as part of the application of Benford's law as a means of a tax authority to object to the correctness of the cash management. Specifically, the frequency distribution of digits in cash book entries was examined using the chi-square test, which resulted in a "strong indication of manipulation of the receipt records". However, the applicability is subject to restrictions and other statistical methods may have to be used (see Benford's law ).
Independence test
The independence test is a significance test for stochastic independence in the contingency table .
We consider two statistical features and , which can be scaled as required . One is interested in whether the features are stochastically independent. It becomes the null hypothesis
- : The features and are stochastically independent.
set up.
method
The observations of are in categories , those of the characteristic in categories . If a characteristic has a large number of characteristics, it is expedient to group them together into classes and to understand the class affiliation as the -th category. There are a total of pairwise observations of and , which are divided into categories.
Conceptually, the test is to be understood as follows:
Consider two discrete random variables and , the common probabilities of which can be represented in a probability table.
You now count how often the -th expression of occurs together with the -th expression of . The observed common absolute frequencies can be entered in a two-dimensional frequency table with rows and columns.
| feature | Sum Σ | ||||||
| feature | 1 | 2 | ... | k | ... | r | n y . |
| 1 | n 11 | n 12 | ... | n 1 k | ... | n 1 r | n 1. |
| 2 | n 21 | n 22 | ... | n 2 k | ... | n 2 r | n 2. |
| ... | ... | ... | ... | ... | ... | ... | ... |
| j | n j1 | ... | ... | n jk | ... | ... | n y. |
| ... | ... | ... | ... | ... | ... | ... | ... |
| m | n m 1 | n m 2 | ... | n mk | ... | n mr | n m . |
| Sum Σ | n .1 | n .2 | ... | n . k | ... | n . r | n |
The row and column sums give the absolute marginal frequencies or as
- and
Correspondingly, the common relative frequencies and the relative marginal frequencies and .
Probability theory applies: If two events and statistically independent, the probability of their common occurrence is equal to the product of the individual probabilities:
One now thinks that analogously to above, with stochastic independence from and , it would also have to apply
with multiplied accordingly
- or
If these differences are small for all of them , one can assume that and are actually stochastically independent.
If one sets for the expected frequency in the presence of independence
the test variable for the independence test results from the above consideration
If the expected frequencies are sufficiently large, the test variable is approximately chi-square distributed with degrees of freedom.
If the test variable is small, the hypothesis is presumed to be true. So is rejected at a high Prüfgrößenwert, the critical region for is right.
At a level of significance , it is rejected if the quantile is the chi-square distribution with degrees of freedom.
particularities
So that the test variable can be viewed as approximately chi-square distributed, every expected frequency must have a certain minimum size. Various textbooks put this at 1 or 5. If the expected frequency is too small, several classes can possibly be combined in order to achieve the minimum size.
Alternatively, the sample distribution of the test statistics can be examined using the bootstrapping method based on the given marginal distributions and the assumption that the characteristics are independent .
Example of the independence test
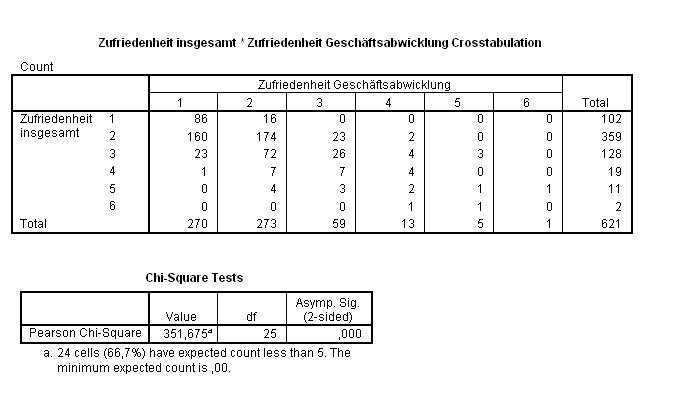
As part of the quality management, the customers of a bank were asked, among other things, about their satisfaction with the business transaction and their overall satisfaction. The degree of satisfaction was based on the school grading system.
The data gives the following cross table of overall satisfaction with bank customers versus their satisfaction with doing business. You can see that some of the expected frequencies were too small.
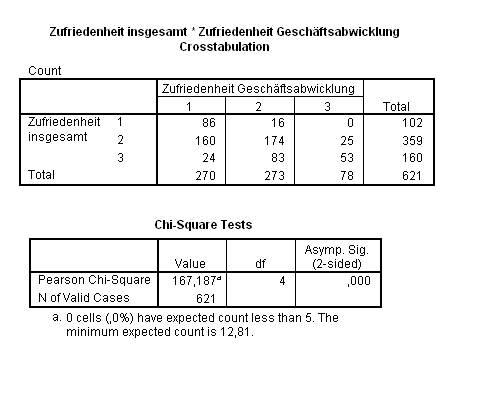
A reduction of the categories to three by combining the grades 3–6 to a new overall grade of 3 yielded methodologically correct results.
The following table contains the expected frequencies , which are calculated as follows:
| feature | ||||
| feature | 1 | 2 | 3 | Σ |
| 1 | 44.35 | 44.84 | 12.81 | 102 |
| 2 | 156.09 | 157.82 | 45.09 | 359 |
| 3 | 69.57 | 70.34 | 20.10 | 160 |
| Σ | 270 | 273 | 78 | 621 |
The test variable is then determined as follows:
For one , the critical value is attached to the test size . Since is, the hypothesis is significantly rejected, so it is assumed that satisfaction with the business transaction and overall satisfaction are associated.
Homogeneity test
With the chi-square homogeneity test , the associated sample distributions can be used to check whether (independent) random samples of discrete features with the sample sizes come from identically distributed (i.e. homogeneous) populations . It is thus helpful in deciding whether several samples come from the same population or distribution, or in deciding whether a characteristic is distributed in the same way in different populations (e.g. men and women). The test, like the other chi-square tests, can be used at any scale level .
The hypotheses are:
- The independent characteristics are distributed identically.
- At least two of the characteristics are distributed differently.
If the distribution function of is indicated with, the hypotheses can also be formulated as follows:
- for at least one
method
The examined random variable (the characteristic), e.g. B. Answer to “the Sunday question ”, be graded, d. That is, there are feature categories (the feature has characteristics), e.g. B. SPD, CDU, B90 / Greens, FDP, Die Linke and Others (i.e., ). The samples can e.g. B. the survey results of various opinion research institutes. It could then be of interest to check whether the survey results differ significantly.
The observed frequencies per sample (survey) and feature category (called party) are in a corresponding - Crosstab entered (here 3 × 3):
| Feature category | ||||
|---|---|---|---|---|
| sample | Category 1 | Category 2 | Category 3 | total |
| total | ||||
The deviations between the observed (empirical) frequency or probability distributions of the samples across the categories of the characteristic are now examined. The observed cell frequencies are compared with the frequencies that would be expected if the null hypothesis were valid.
The cell frequencies expected under the validity of the null hypothesis of a homogeneous population are determined from the marginal distributions:
denotes the expected number of observations (absolute frequency) from sample in category .
On the basis of the values calculated in this way, the following approximately chi-square distributed test value is calculated:
In order to arrive at a test decision, the value obtained for the test variable is compared with the associated critical value; H. with the quantile of the chi-square distribution that depends on the number of degrees of freedom and the level of significance (alternatively, the p-value can be determined). If the deviations between at least two sample distributions are significant, the null hypothesis is rejected; H. the null hypothesis of homogeneity is rejected if
- .
The rejection range for is to the right of the critical value.
Conditions of use
So that the test variable can be viewed as approximately ( approximately ) chi-square distributed, the following approximation conditions must apply:
- "Large" sample size ( )
- for all
- min. 80% of the
- Rinne (2003) and Voss (2000) also call for cell frequencies
If some of the expected frequencies are too small, several classes or feature categories must be combined in order to comply with the approximation conditions.
Does the random variable being examined have a large number of (possible) characteristics, e.g. B. because the variable is metrically continuous, it is expedient to summarize it in classes (= categories) so that the now classified random variable can be examined with the chi-square test. It should be noted, however, that the way the observations are classified can influence the test result.
Comparison to independence and distribution test
The homogeneity test can also be interpreted as an independence test if the samples are viewed as expressions of a second characteristic. It can also be viewed as a form of distribution test that compares not one empirical and one theoretical distribution, but rather several empirical distributions. However, the independence test and distribution test are one-sample problems, while the homogeneity test is a multiple-sample problem. In the independence test, a single sample is taken with regard to two characteristics, and in the case of the distribution test, a sample is taken with regard to one characteristic. In the homogeneity test, several random samples are taken with regard to a characteristic.
Four-field test
The chi-square four-field test is a statistical test . It is used to check whether two dichotomous features are stochastically independent of one another or whether the distribution of a dichotomous feature in two groups is identical.
method
The four-field test is based on a (2 × 2) contingency table that visualizes the (bivariate) frequency distribution of two characteristics :
| Feature X | |||
|---|---|---|---|
| Feature Y | Expression 1 | Expression 2 | Line total |
| Expression 1 | a | b | a + b |
| Expression 2 | c | d | c + d |
| Column total | a + c | b + d | n = a + b + c + d |
According to a rule of thumb , the expected value of all four fields must be at least 5. The expected value is calculated from the row total * column total / total number. If the expected value is less than 5, statisticians recommend the Fisher's exact test .
Test statistics
In order to test the null hypothesis that both features are stochastically independent, the following test variable is first calculated for a two-sided test:
- .
The test variable is approximately chi-square distributed with one degree of freedom. It should only be used if each of the two samples contains at least six carriers of characteristics (observations).
Test decision
If the test value obtained on the basis of the sample is smaller than the critical value belonging to the selected significance level (i.e. the corresponding quantile of the chi-square distribution), then the test could not prove that there was a significant difference. If, on the other hand, a test value is calculated that is greater than or equal to the critical value, there is a significant difference between the samples.
The probability that the calculated (or an even larger) test value was only obtained by chance due to the sampling (p-value) can be calculated approximately as follows:
The approximation of this (rule of thumb) formula to the actual p-value is good if the test variable is between 2.0 and 8.0.
Examples and Applications
When asked whether a medical measure is effective or not, the four-field test is very helpful because it focuses on the main decision criterion.
example 1
50 (randomly selected) women and men are asked whether they smoke or not.
The result is:
- Women: 25 smokers, 25 non-smokers
- Men: 30 smokers, 20 non-smokers
If a four-field test is carried out on the basis of this survey, the formula shown above results in a test value of approx. 1. Since this value is smaller than the critical value 3.841, the null hypothesis that smoking behavior is independent of gender can not be rejected become. The proportion of smokers and non-smokers does not differ significantly between the sexes.
Example 2
500 (randomly selected) women and men are asked whether they smoke or not.
The following data is received:
- Women: 250 non-smokers, 250 smokers
- Men: 300 non-smokers, 200 smokers
The four-field test results in a test value of greater than 3.841. Since the null hypothesis that the characteristics “smoking behavior” and “gender” are stochastically independent of one another can be rejected at a significance level of 0.05.
Table of the quantiles of the chi-square distribution
The table shows the most important quantiles of the chi-square distribution . The degrees of freedom are entered in the left column and the levels in the top line . Reading example: The quantile of the chi-square distribution with 2 degrees of freedom and a level of 1% is 9.21.
1 − α 0.900 0.950 0.975 0.990 0.995 0.999 1 2.71 3.84 5.02 6.63 7.88 10.83 2 4.61 5.99 7.38 9.21 10.60 13.82 3 6.25 7.81 9.35 11.34 12.84 16.27 4th 7.78 9.49 11.14 13.28 14.86 18.47 5 9.24 11.07 12.83 15.09 16.75 20.52 6th 10.64 12.59 14.45 16.81 18.55 22.46 7th 12.02 14.07 16.01 18.48 20.28 24.32 8th 13.36 15.51 17.53 20.09 21.95 26.12 9 14.68 16.92 19.02 21.67 23.59 27.88 10 15.99 18.31 20.48 23.21 25.19 29.59 11 17.28 19.68 21.92 24.72 26.76 31.26 12 18.55 21.03 23.34 26.22 28.30 32.91 13 19.81 22.36 24.74 27.69 29.82 34.53 14th 21.06 23.68 26.12 29.14 31.32 36.12 15th 22.31 25.00 27.49 30.58 32.80 37.70 16 23.54 26.30 28.85 32.00 34.27 39.25 17th 24.77 27.59 30.19 33.41 35.72 40.79 18th 25.99 28.87 31.53 34.81 37.16 42.31 19th 27.20 30.14 32.85 36.19 38.58 43.82 20th 28.41 31.41 34.17 37.57 40.00 45.31 21st 29.62 32.67 35.48 38.93 41.40 46.80 22nd 30.81 33.92 36.78 40.29 42.80 48.27 23 32.01 35.17 38.08 41.64 44.18 49.73 24 33.20 36.42 39.36 42.98 45.56 51.18 25th 34.38 37.65 40.65 44.31 46.93 52.62 26th 35.56 38.89 41.92 45.64 48.29 54.05 27 36.74 40.11 43.19 46.96 49.64 55.48 28 37.92 41.34 44.46 48.28 50.99 56.89 29 39.09 42.56 45.72 49.59 52.34 58.30 30th 40.26 43.77 46.98 50.89 53.67 59.70 40 51.81 55.76 59.34 63.69 66.77 73.40 50 63.17 67.50 71.42 76.15 79.49 86.66 60 74.40 79.08 83.30 88.38 91.95 99.61 70 85.53 90.53 95.02 100.43 104.21 112.32 80 96.58 101.88 106.63 112.33 116.32 124.84 90 107.57 113.15 118.14 124.12 128.30 137.21 100 118.50 124.34 129.56 135.81 140.17 149.45 200 226.02 233.99 241.06 249.45 255.26 267.54 300 331.79 341.40 349.87 359.91 366.84 381.43 400 436.65 447.63 457.31 468.72 476.61 493.13 500 540.93 553.13 563.85 576.49 585.21 603.45
Alternatives to the chi-square test
The chi-square test is still widely used, although better alternatives are available today. The test statistics are particularly problematic with small values per cell (rule of thumb:) , while the chi-square test is still reliable with large samples.
The original advantage of the chi-square test was that the test statistics can also be calculated by hand, especially for smaller tables, because the most difficult calculation step is squaring, while the more precise G-test, the most difficult calculation step, requires logarithmization. The test statistic is approximately distributed chi-square and is also robust when the contingency table contains rare events.
In computational linguistics , the G-Test has been able to establish itself, since the frequency analysis of rarely occurring words and text modules is a typical problem there.
Since today's computers offer enough computing power, both tests can be replaced by Fisher's exact test .
See also
Web links
- Calculator for simple and cumulative probabilities as well as quantiles and confidence intervals of the chi-square distribution
- Article on the problem of the one- and two-sided chi-square significance test
- Exact p-values (English)
Four field test:
Individual evidence
- ^ Karl Pearson: On the criterion that a given system of derivations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling . In: The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . tape 50 , no. 5 , 1900, pp. 157-175 , doi : 10.1080 / 14786440009463897 .
- ↑ Decision of the FG Münster from November 10, 2003 (Ref .: 6 V 4562/03 E, U) (PDF)
- ↑ Horst Rinne: Pocket book of statistics . 3. Edition. Verlag Harri Deutsch, 2003, p. 562-563 .
- ↑ Bernd Rönz, Hans G. Strohe: Lexikon Statistics , Gabler Verlag, 1994, p. 69.
- ↑ see Political Parties in Germany
- ↑ a b Horst Rinne: Pocket book of statistics . 3. Edition. Verlag Harri Deutsch, 2003, p. 562 .
- ↑ a b c Werner Voss: Pocket book of statistics . 1st edition. Fachbuchverlag Leipzig, 2000, p. 447 .
- ^ Jürgen Bortz, Nicola Döring: Research methods and evaluation for human and social scientists . 4th edition. Springer, 2006, p. 103 .
- ^ Hans-Hermann Dubben, Hans-Peter Beck-Bornholdt: The dog who lays eggs . 4th edition. Rowohlt Science, 2009, p. 293 .