Correlation coefficient

The correlation coefficient, also known as the product-moment correlation, is a measure of the degree of the linear relationship between two at least interval-scaled features , which does not depend on the units of measurement and is therefore dimensionless. It can assume values ​​between and . With a value of (or ) there is a completely positive (or negative) linear relationship between the characteristics under consideration. If the correlation coefficient has the value , then the two features are not linearly related at all. However, regardless of this, they can depend on one another in a non-linear manner. The correlation coefficient is therefore not a suitable measure for the (pure) stochastic dependence on features. The square of the correlation coefficient represents the coefficient of determination . The correlation coefficient was first used by the British naturalist Sir Francis Galton (1822-1911) in the 1870s. Karl Pearson finally provided a formal mathematical justification for the correlation coefficient. Since it was popularized by Auguste Bravais and Pearson, the correlation coefficient is also called the Pearson correlation or Bravais-Pearson correlation . ${\displaystyle -1}$ ${\displaystyle +1}$ ${\displaystyle +1}$ ${\displaystyle -1}$ ${\displaystyle 0}$

Depending on whether the linear relationship between simultaneous measured values ​​of two different characteristics or that between measured values ​​of a single characteristic that differ over time is considered, one speaks of either cross-correlation or cross- autocorrelation (see also time series analysis ).

Correlation coefficients were developed several times - as already by Ferdinand Tönnies  - today that of Pearson is generally used.

Definitions

Correlation coefficient for random variables

construction

As a starting point for the construction of the correlation coefficient for two random variables and consider the two standardized random variables (related to the standard deviation) and . The covariance of these standardized random variables results from the set for linear transformations of covariances through ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle {\tilde {X}}=(X-\mu _{X})/\sigma _{X}}$ ${\displaystyle {\tilde {Y}}=(Y-\mu _{Y})/\sigma _{Y}}$

${\displaystyle \operatorname {Cov} ({\tilde {X}},{\tilde {Y}})={\frac {1}{\sigma _{X}\sigma _{Y}}}\operatorname {Cov} (X,Y)=\rho _{X,Y}}$.

The correlation coefficient can be understood as the covariance of the standardized random variables and . ${\displaystyle {\tilde {X}}}$ ${\displaystyle {\tilde {Y}}}$

definition

For two square integrable random variables and each with a positive standard deviation or and covariance , the correlation coefficient (Pearson's measure of correlation coefficient) is defined by: ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \sigma _{X}}$ ${\displaystyle \sigma _{Y}}$ ${\displaystyle \operatorname {Cov} (X,Y)}$

${\displaystyle \operatorname {Korr} (X,Y)={\frac {\operatorname {Cov} (X,Y)}{{\sqrt {\operatorname {Var} (X)}}{\sqrt {\operatorname {Var} (Y)}}}}={\frac {\sigma _{X,Y}}{\sigma _{X}\sigma _{Y}}}=:\rho _{X,Y}}$.

This correlation coefficient is also called the population correlation coefficient . By defining the stochastic variance and covariance , the correlation coefficient for random variables can also be represented as follows

${\displaystyle \operatorname {Korr} (X,Y)={\frac {\operatorname {E} \left((X-\operatorname {E} (X))(Y-\operatorname {E} (Y))\right)}{\sqrt {\operatorname {E} \left((X-\operatorname {E} (X))^{2}\right)\operatorname {E} \left((Y-\operatorname {E} (Y))^{2}\right)}}}}$,

where represents the expected value . ${\displaystyle \operatorname {E} (\cdot )}$

Furthermore, they are called uncorrelated if applies. For positive and that is exactly the case when is. If they are independent , then they are also uncorrelated; the converse is generally not true. ${\displaystyle X,Y}$ ${\displaystyle \operatorname {Cov} (X,Y)=0}$ ${\displaystyle \sigma _{X}}$ ${\displaystyle \sigma _{Y}}$ ${\displaystyle \rho _{X,Y}=0}$ ${\displaystyle X,Y}$

estimate

In the context of inductive statistics , one is interested in an unbiased estimate of the correlation coefficient of the population . Therefore, unbiased estimates of the variances and covariance are inserted into the population correlation coefficient formula . This leads to the sample correlation coefficient : ${\displaystyle {\hat {\rho }}_{X,Y}}$ ${\displaystyle \rho _{X,Y}}$

${\displaystyle R_{X,Y}:={\frac {S_{X,Y}}{S_{X}S_{Y}}}={\frac {\sum _{i=1}^{n}(X_{i}-{\overline {X}})(Y_{i}-{\overline {Y}})}{\sqrt {\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}\sum _{i=1}^{n}(Y_{i}-{\overline {Y}})^{2}}}}}$.

Empirical correlation coefficient

Let be a two-dimensional sample of two cardinally scaled features with the empirical means and the sub-samples  and . Furthermore, for the empirical variances and the partial samples, the following applies . Then the empirical correlation coefficient - analogous to the correlation coefficient for random variables, except that instead of the theoretical moments, the empirical covariance and the empirical variances - are defined by: ${\displaystyle (x_{i},y_{i})^{\top },\;i=1,\ldots ,n}$ ${\displaystyle \textstyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$ ${\displaystyle \textstyle {\overline {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}$ ${\displaystyle x=(x_{1},\ldots ,x_{n})^{\top }}$ ${\displaystyle y=(y_{1},\ldots ,y_{n})^{\top }}$ ${\displaystyle s_{x}^{2}:=\textstyle {\tfrac {1}{n-1}}\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$ ${\displaystyle s_{y}^{2}:=\textstyle {\tfrac {1}{n-1}}\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}$ ${\displaystyle s_{x}^{2}s_{y}^{2}\neq 0}$

${\displaystyle r_{x,y}:={\frac {\sum _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}{\sqrt {\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}}={\frac {SP_{x,y}}{\sqrt {SQ_{x}SQ_{y}}}}}$

Different values ​​of the correlation coefficient

Here is the sum of the squared deviations and the sum of the deviation products . ${\displaystyle SQ_{x}}$ ${\displaystyle SP_{x,y}}$

Using the empirical covariance and the empirical standard deviations ${\displaystyle s_{x,y}:={\tfrac {1}{n-1}}\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}$

${\displaystyle s_{x}:={\sqrt {{\tfrac {1}{n-1}}\sum \nolimits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}}}\quad }$ and ${\displaystyle \quad s_{y}:={\sqrt {{\tfrac {1}{n-1}}\sum \nolimits _{i=1}^{n}\left(y_{i}-{\overline {y}}\right)^{2}}}}$

of the partial samples and the following representation results: ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle r_{x,y}:={\frac {s_{x,y}}{s_{x}s_{y}}}}$.

If these measurement series values ​​are z-transformed , i.e. , where the unbiased estimate denotes the variance , the following also applies: ${\displaystyle z_{i}:={\tfrac {x_{i}-{\overline {x}}}{s_{x}}}}$ ${\displaystyle s_{x}}$

${\displaystyle {\hat {\rho }}={\frac {1}{n-1}}\sum z_{x}z_{y}}$.

Since one only wants to describe the relationship between two variables in descriptive statistics as normalized mean common scatter in the sample, the correlation is also calculated as

${\displaystyle r_{x,y}:={\frac {{\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}{{\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}\cdot {\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}}}}$.

Since the factors or are removed from the formulas, the value of the coefficient is the same in both cases. ${\displaystyle {\tfrac {1}{n}}}$ ${\displaystyle {\tfrac {1}{n-1}}}$

A "simplification" of the above formula to make it easier to calculate a correlation is as follows:

${\displaystyle r_{x,y}:={\frac {n\sum _{i=1}^{n}(x_{i}\cdot y_{i})-(\sum _{i=1}^{n}x_{i})\cdot (\sum _{i=1}^{n}y_{i})}{\sqrt {\left[n\sum _{i=1}^{n}x_{i}^{2}-(\sum _{i=1}^{n}x_{i})^{2}\right]\cdot \left[n\sum _{i=1}^{n}y_{i}^{2}-(\sum _{i=1}^{n}y_{i})^{2}\right]}}}}$

However, this transformation of the formula is numerically unstable and should therefore not be used with floating point numbers if the mean values ​​are not close to zero.

example

Scatter plot with means and the value of the correlation coefficient

The values ​​in the table below are given in the second and third columns for the eleven observation pairs. The mean values result from and and thus the fourth and fifth columns of the table can be calculated. The sixth column contains the product of the fourth and the fifth column and thus results . The last two columns contain the squares of the fourth and fifth columns and the result is and . ${\displaystyle (x_{i},y_{i})}$ ${\displaystyle {\overline {x}}=99/11=9{,}0}$ ${\displaystyle {\overline {y}}=82{,}51/11=7{,}5}$ ${\displaystyle \sum _{i=1}^{11}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})=55{,}01}$ ${\displaystyle \sum _{i=1}^{11}(x_{i}-{\overline {x}})^{2}=110{,}00\;}$ ${\displaystyle \;\sum _{i=1}^{11}(y_{i}-{\overline {y}})^{2}=41{,}27}$

This results in the correlation . ${\displaystyle r_{x,y}={\frac {55{,}01}{{\sqrt {110{,}00}}{\sqrt {41{,}27}}}}=0{,}816}$

${\displaystyle i}$	${\displaystyle x_{i}}$	${\displaystyle y_{i}}$	${\displaystyle x_{i}-{\overline {x}}}$	${\displaystyle y_{i}-{\overline {y}}}$	${\displaystyle (x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}$	${\displaystyle (x_{i}-{\overline {x}})^{2}}$	${\displaystyle (y_{i}-{\overline {y}})^{2}}$
1	10.00	8.04	1.00	0.54	0.54	1.00	0.29
2	8.00	6.95	−1.00	−0.55	0.55	1.00	0.30
3	13.00	7.58	4.00	0.08	0.32	16.00	0.01
4th	9.00	8.81	0.00	1.31	0.00	0.00	1.71
5	11.00	8.33	2.00	0.83	1.66	4.00	0.69
6th	14.00	9.96	5.00	2.46	12.30	25.00	6.05
7th	6.00	7.24	−3.00	−0.26	0.78	9.00	0.07
8th	4.00	4.26	−5.00	−3.24	16.20	25.00	10.50
9	12.00	10.84	3.00	3.34	10.02	9.00	11.15
10	7.00	4.82	−2.00	−2.68	5.36	4.00	7.19
11	5.00	5.68	−4.00	−1.82	7.28	16.00	3.32
${\displaystyle \Sigma }$	99.00	82.51			55.01	110.00	41.27
All values ​​in the table are rounded to two decimal places!

properties

With the definition of the correlation coefficient applies immediately

• ${\displaystyle \operatorname {Korr} (X,Y)=\operatorname {Korr} (Y,X)\;}$ or. ${\displaystyle \;r_{x,y}=r_{y,x}}$
• ${\displaystyle \operatorname {Korr} (X,X)=1}$.
• ${\displaystyle \operatorname {Korr} (aX+b,Y)=\operatorname {sgn}(a)\cdot \operatorname {Korr} (X,Y)}$for , ${\displaystyle a,b\in \mathbb {R} }$

where is the signum function . ${\displaystyle \operatorname {sgn} }$

The Cauchy-Schwarz inequality shows that

• ${\displaystyle \operatorname {Korr} (X,Y)\in [-1,1]}$.

You can see that almost certainly exactly when . One sees it, for example, by solving. In that case is and . ${\displaystyle Y=aX+b}$ ${\displaystyle |\operatorname {Korr} (X,Y)|=1}$ ${\displaystyle \operatorname {E} ((X-aY-b)^{2})=0}$ ${\displaystyle a=\operatorname {Korr} (X,Y)\cdot {\frac {\sigma _{y}}{\sigma _{X}}}}$ ${\displaystyle b=\operatorname {E} (Y)-a\cdot \operatorname {E} (X)}$

If the random variables and are stochastically independent of each other , then: ${\displaystyle X}$ ${\displaystyle Y}$

• ${\displaystyle \operatorname {Korr} (X,Y)=0}$.

However, the reverse is not permissible because there may be dependency structures that the correlation coefficient does not capture. For the multivariate normal distribution , however, the following applies: The random variables and are stochastically independent if and only if they are uncorrelated. It is important here that and are normally distributed together. It is not enough that and are normally distributed in each case. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

Requirements for the Pearson Correlation

The Pearson correlation coefficient allows statements to be made about statistical relationships under the following conditions:

Scaling

The Pearsonian correlation coefficient provides correct results for interval-scaled and dichotomous data. Other correlation concepts (e.g. rank correlation coefficients ) exist for lower scalings .

Normal distribution

To carry out standardized significance tests using the correlation coefficient in the population , both variables must be approximately normally distributed . In the event of excessive deviations from the normal distribution, the rank correlation coefficient must be used. (Alternatively, if the distribution is known, you can use adapted (non-standardized) significance tests.)

Linearity condition

A linear relationship is assumed between the variables and . This condition is often ignored in practice; this sometimes explains disappointingly low correlations, although the relationship between and is still high at times. A simple example of a high correlation despite a low correlation coefficient is the Fibonacci sequence . All numbers in the Fibonacci sequence are precisely determined by their position in the series using a mathematical formula (see Binet's formula ). The relationship between the position number of a Fibonacci number and the size of the number is completely determined. Nevertheless, the correlation coefficient between the ordinal numbers of the first 360 Fibonacci numbers and the numbers in question is only 0.20; this means that in a first approximation not much more than the variance can be explained by the correlation coefficient and 96% of the variance remains “unexplained” . The reason is the neglect of the linearity condition, because the Fibonacci numbers grow progressively: In such cases the correlation coefficient cannot be interpreted correctly. A possible alternative that does without the requirement of linearity of the relationship is transinformation . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle 0{,}2^{2}=4\;\%}$

Significance condition

A correlation coefficient> 0 in the case of a positive correlation or <0 in the case of a negative correlation between and does not justify the a priori statement that there is a statistical relationship between and . Such a statement is only valid if the correlation coefficient determined is significant . The term “significant” here means “significantly different from zero”. The higher the number of value pairs and the significance level, the lower the absolute value of a correlation coefficient may be in order to justify the statement that there is a linear relationship between and . A t-test shows whether the deviation of the determined correlation coefficient from zero is also significant. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle (x,y)}$ ${\displaystyle x}$ ${\displaystyle y}$

Pictorial representation and interpretation

Different point clouds together with the Pearson's correlation coefficient that can be calculated for each of them. Note that the latter reflects the scattering of the point cloud and the general direction of the linear dependence on and (top row), but not its steepness (middle row). For example, if the point cloud runs exactly horizontally (middle image), no correlation coefficient at all can be calculated. Another weak point of Pearson's correlation coefficient are non-linear dependencies (lower line), which can usually not be captured at all or only inadequately with the help of this coefficient. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \operatorname {Var} (Y)=0}$

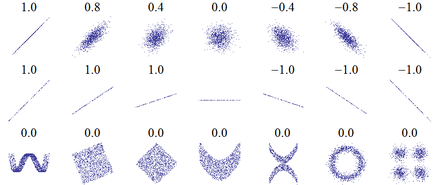
If two features are fully correlated with one another (i.e. ), then all measured values ​​lie in a 2-dimensional coordinate system on a straight line. With a perfect positive correlation ( ) the straight line rises. If the features are perfectly negatively correlated with each other ( ), the line sinks. If there is a very high correlation between two characteristics, it is often said that they explain the same thing. ${\displaystyle |r|=1}$ ${\displaystyle r=+1}$ ${\displaystyle r=-1}$

The closer the amount is to 0, the smaller the linear relationship. For , the statistical relationship between the measured values ​​can no longer be represented by a clearly rising or falling straight line. This is e.g. This is the case, for example, when the measured values ​​are distributed rotationally symmetrically around the center point. Nevertheless, there can then be a non-linear statistical relationship between the features. Conversely, however, the following applies: If the characteristics are statistically independent, the correlation coefficient always takes the value 0. ${\displaystyle r}$ ${\displaystyle r=0}$

The correlation coefficient is not an indication of a causal (i.e. causal) connection between the two features: the settlement by storks in southern Burgenland does correlate positively with the number of births of the residents there, but that does not yet mean a “causal connection”, but it is still a “statistical connection “Given. However, this is derived from another, further factor, as can be explained in the example by industrialization or the increase in prosperity, which on the one hand restricted the habitat of the storks and on the other hand led to a reduction in the number of births. Correlations of this type are called spurious correlations .

The correlation coefficient cannot be an indication of the direction of a relationship : Does the precipitation increase due to the higher evaporation or does the evaporation increase because the precipitation supplies more water? Or are both mutually dependent, i.e. possibly in both directions?

Whether a measured correlation coefficient is interpreted as large or small depends heavily on the type of data examined. In psychological examinations, values ​​ab count as small, medium and large effects. ${\displaystyle |r|=0{,}1}$ ${\displaystyle |r|=0{,}3}$ ${\displaystyle |r|=0{,}5}$

The square of the correlation coefficient is called the coefficient of determination . As a first approximation, it indicates what percentage of the variance , i.e. H. Dispersion of one variable can be explained by the dispersion of the other variable. Example: With r = 0.3, 9% (= 0.3² = 0.09) of the total occurring variance is explained in terms of a statistical relationship. ${\displaystyle r^{2}}$

Fisher transformation

Empirical correlation coefficients are not normally distributed. Before calculating the confidence intervals , the distribution must therefore first be corrected using the Fisher transformation. If the data and of an at least approximately bivariate normal distribution derived population, the empirical correlation coefficient is quite steep unimodal distribution. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle {\hat {\rho }}}$

The Fisher transform of the correlation coefficient is then: ${\displaystyle {\hat {\rho }}}$

${\displaystyle z:=f({\hat {\rho }})=0{,}5\cdot \ln \left({\frac {1+{\hat {\rho }}}{1-{\hat {\rho }}}}\right)=\operatorname {artanh} ({\hat {\rho }})\,}$

${\displaystyle z}$is approximately normally distributed with the standard deviation and mean ${\displaystyle 1/{\sqrt {n-3}}}$

${\displaystyle {1 \over 2}\ln \left({{1+\rho } \over {1-\rho }}\right),}$

where stands for the correlation coefficient of the population. The probability, calculated on the basis of this normal distribution, that the mean value is enclosed by the two limits and ${\displaystyle \rho }$ ${\displaystyle z_{1}}$ ${\displaystyle z_{2}}$

${\displaystyle P\left(\underbrace {f(r)-{\frac {z_{1-\alpha /2}}{\sqrt {n-3}}}} _{z_{1}}\leq \mu \leq \underbrace {f(r)+{\frac {z_{1-\alpha /2}}{\sqrt {n-3}}}} _{z_{2}}\right)=1-\alpha }$,

and is then retransformed to

${\displaystyle {\begin{aligned}r_{1}&=(e^{2z_{1}}-1)/(e^{2z_{1}}+1)\\r_{2}&=(e^{2z_{2}}-1)/(e^{2z_{2}}+1).\end{aligned}}}$

The confidence interval for the correlation is then ${\displaystyle (1-\alpha )}$

${\displaystyle r_{1}\leq {\hat {\rho }}\leq r_{2}}$.

Confidence intervals of correlations are usually asymmetrical with respect to their mean.

Test of the correlation coefficient / enhancer Z-test

The following tests ( Steigers Z-Test ) can be carried out if the variables and have an approximately bivariate normal distribution: ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle H_{0}\colon \rho =\rho _{0}\;}$ vs. ${\displaystyle \;H_{1}\colon \rho \neq \rho _{0}}$	(two-sided hypothesis)
${\displaystyle H_{0}\colon \rho \leq \rho _{0}\;}$ vs. ${\displaystyle \;H_{1}\colon \rho >\rho _{0}}$	(right-hand hypothesis)
${\displaystyle H_{0}\colon \rho \geq \rho _{0}\;}$ vs. ${\displaystyle \;H_{1}\colon \rho <\rho _{0}}$	(left-hand hypothesis)

The test statistic is

${\displaystyle T(r)={\frac {f(r)-f(\rho _{0})-\rho _{0}/(n-2)}{1/{\sqrt {n-3}}}}\sim {\mathcal {N}}(0,1)}$

standard normal distribution ( is the Fisher transform, see previous section). ${\displaystyle f(\cdot )}$

In the special case of the hypothesis vs. the test statistic results as t-distributed with degrees of freedom : ${\displaystyle H_{0}\colon \rho =0}$ ${\displaystyle H_{1}\colon \rho \neq 0}$ ${\displaystyle (n-2)}$

${\displaystyle T_{0}(r)={\frac {r{\sqrt {n-2}}}{\sqrt {1-r^{2}}}}\sim t(n-2)}$.

Partial correlation coefficient

The following graphic shows an example: There is a noticeable correlation between and . If you look at the two point clouds on the right, you can see that and each have a strong correlation. The observed correlation between and is now based almost exclusively on this effect. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle U}$ ${\displaystyle X}$ ${\displaystyle Y}$

A correlation between two random variables and can possibly be traced back to a common influence of a third random variable . To measure such an effect, there is the concept of partial correlation (also called partial correlation). The “partial correlation of and under ” is given by ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle U}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle U}$

${\displaystyle r_{(X,Y)/U}={\frac {r_{X,Y}-r_{XU}\cdot r_{Y,U}}{\sqrt {(1-r_{XU}^{2})(1-r_{YU}^{2})}}}.}$

Example from everyday life:

In a company, employees are selected at random and their height is determined. In addition, each respondent must indicate his income. The result of the study is that height and income have a positive correlation, i.e. taller people also earn more. On closer examination, however, it turns out that the connection can be traced back to the third variable gender. On average, women are shorter than men, but they also often earn less . If one now calculates the partial correlation between income and body size while controlling for gender, the relationship disappears. For example, taller men do not earn more than shorter men. This example is fictional and more complicated in reality, but it can illustrate the idea of ​​partial correlation.

Robust correlation coefficients

The Pearson's correlation coefficient is sensitive to outliers . Therefore, various robust correlation coefficients have been developed, e.g. B.

• Rank correlation coefficients that use ranks instead of the observation values (such as Spearman's rank correlation coefficient (Spearman's Rho) and Kendall's rank correlation coefficient (Kendall's tau)) or
• the quadrant correlation.

Quadrant correlation

The quadrant correlation results from the number of observations in the four quadrants determined by the median pair. This includes how many of the observations are in quadrants I and III ( ) or how many are in quadrants II and IV ( ). The observations in quadrants I and III each provide a contribution from and the observations in quadrants II and IV from : ${\displaystyle N_{+}}$ ${\displaystyle N_{-}}$ ${\displaystyle +1/n}$ ${\displaystyle -1/n}$

${\displaystyle r_{\text{quad}}={\frac {N_{+}-N_{-}}{N_{+}+N_{-}}}={\frac {1}{n}}\sum _{i=1}^{n}\operatorname {sgn}(x_{i}-{\tilde {x}})\operatorname {sgn}(y_{i}-{\tilde {y}})}$

with the signum function , the number of observations and the medians of the observations. Since each value is either , or , it doesn't matter how far an observation is from the medians. ${\displaystyle \operatorname {sgn}(\cdot )}$ ${\displaystyle n}$ ${\displaystyle {\tilde {x}}}$ ${\displaystyle {\tilde {y}}}$ ${\displaystyle \operatorname {sgn}(x_{i}-{\tilde {x}})\operatorname {sgn}(y_{i}-{\tilde {y}})}$ ${\displaystyle -1}$ ${\displaystyle 0}$ ${\displaystyle +1}$

Using the median test, the hypotheses vs. be checked. If the number of observations is with , the number of observations with and , then the following test statistic is chi-square distributed with one degree of freedom: ${\displaystyle H_{0}:r_{\text{quad}}=0\,}$ ${\displaystyle H_{1}:r_{\text{quad}}\neq 0}$ ${\displaystyle n_{+}}$ ${\displaystyle \operatorname {sgn}(x_{i}-{\tilde {x}})\operatorname {sgn}(y_{i}-{\tilde {y}})=+1}$ ${\displaystyle n_{-}}$ ${\displaystyle \operatorname {sgn}(x_{i}-{\tilde {x}})\operatorname {sgn}(y_{i}-{\tilde {y}})=-1}$ ${\displaystyle n_{e}=(n_{+}+n_{-})/2>5}$

${\displaystyle {\frac {(n_{+}-n_{e})^{2}+(n_{-}-n_{e})^{2}}{n_{e}}}\sim \chi ^{2}(1)}$.

Estimating the correlation between non-scale variables

The estimation of the correlation with the correlation coefficient according to Pearson assumes that both variables are interval-scaled and normally distributed . In contrast, the rank correlation coefficients can always be used to estimate the correlation if both variables are at least ordinally scaled . The correlation between a dichotomous and an interval-scaled and normally distributed variable can be estimated using the point-biserial correlation . The correlation between two dichotomous variables can be estimated using the four-field correlation coefficient . Here one can make the distinction that with two naturally dichotomous variables, the correlation can be calculated both by the odds ratio and by the Phi coefficient . A correlation of two ordinally or one interval and one ordinally measured variable can be calculated using Spearman's rho or Kendall's tau.

See also

• Measure of connection
• Correlation matrix
• correlation
• Contingency coefficient

literature

• Francis Galton: Co-relations and their measurement, chiefly from anthropometric data . In: Proceedings of the Royal Society . tape 45 , no. 13 , December 5, 1888, pp. 135–145 ( galton.org [PDF; accessed September 12, 2012]).
• Birk Diedenhofen, Jochen Musch: cocor : A Comprehensive Solution for the Statistical Comparison of Correlations. 2015. PLoS ONE, 10 (4): e0121945
• Joachim Hartung: Statistics. 12th edition, Oldenbourg Verlag 1999, p. 561 f., ISBN 3-486-24984-3
• Peter Zöfel: Statistics for psychologists. Pearson Studium 2003, Munich, p. 154.

Web links

Wiktionary: Correlation coefficient  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Simple explanation of the correlation coefficient  - learning and teaching materials

Wikibooks:: Mathematics for School ${\displaystyle {\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$

• Comprehensive explanation of various correlation coefficients and their requirements, as well as common application errors
• Eric W. Weisstein : Correlation Coefficient . In: MathWorld (English). Representation of the correlation coefficient as a least squares estimator
• cocor - A free web interface and R package for the statistical comparison of two dependent or independent correlations with overlapping or non-overlapping variables

Individual evidence

1. ↑ The name product-moment correlation for the correlation coefficient for random variables comes from the fact that the covariance is related to the product of the variances - which represent moments in the sense of stochastics - of and . ${\displaystyle \rho _{X,Y}}$ ${\displaystyle X}$ ${\displaystyle Y}$
2. ↑ Franka Miriam Brückler: History of Mathematics compact. The most important things from analysis, probability theory, applied mathematics, topology and set theory. Springer-Verlag, 2017, ISBN 978-3-662-55573-6 , p. 116.
3. ↑ L. Fahrmeir, R. Künstler among others: Statistics. The way to data analysis. 8th edition. Springer 2016, p. 326.
4. ↑ Bayer, Hackel: Probability Theory and Mathematical Statistics , p. 86.
5. ↑ Torsten Becker, et al .: Stochastic risk modeling and statistical methods. Springer Spectrum, 2016. p. 79.
6. ↑ Jürgen Bortz, Christof Schuster: Statistics for human and social scientists . 7th edition. Springer-Verlag GmbH, Berlin / Heidelberg / New York 2010, ISBN 978-3-642-12769-4 , p. 157 .
7. ↑ Erich Schubert, Michael Gertz: Numerically stable parallel computation of (co-) variance . ACM, 2018, ISBN 978-1-4503-6505-5 , pp. 10 , doi : 10.1145 / 3221269.3223036 ( acm.org [accessed August 7, 2018]).
8. ^ Jacob Cohen: A power primer. In: Psychological Bulletin . tape 112 , no. 1 , 1992, ISSN  1939-1455 , pp. 155–159 , doi : 10.1037 / 0033-2909.112.1.155 ( apa.org [accessed April 30, 2020]).
9. ^ Jacob Cohen: A power primer. Accessed April 30, 2020 (English). 
10. ^ JH Steiger: Tests for comparing elements of a correlation matrix. 1980. Psychological Bulletin , 87, 245-251, doi : 10.1037 / 0033-2909.87.2.245 .
11. ↑ The influence of body size on wage level and career choice: Current research status and new results based on the microcensus.