Isoparametric elements

Isoparametric elements are formulations for finite elements used in the finite element method (FEM), which are widely used in the analysis of solids. The FEM is a numerical method for the solution of differential equations whose unique solution requires certain additional conditions, so-called initial and boundary conditions . The solution of the initial boundary value problem is developed in the FEM in approach functions that are potentially able to approximate every solution function allowed for comparison. A discretization error occurs due to the limitation of the shape functions to a finite number . Now the solution is split additively into two parts: one that reflects the initial condition and the other that has to be adapted to the boundary conditions. Now one could approximate these two parts with different shape functions. The special thing about the isoparametric elements is that they use the same approach functions for both parts of the solution . The standard formulation of the FEM is the displacement method . In order to be able to represent a location-independent displacement field there, the approach functions must meet certain requirements that are particularly easy to meet in isoparametric elements. Isoparametric elements have the advantages that

1. they can be used in most problems,
2. a constant displacement field can be easily represented in them,
3. the discretization error can be easily assessed visually in the preprocessor and
4. only one set of approach functions needs to be defined and programmed.

Solution of differential equations

The FEM is a method for the solution of differential equations (Dgl) and therefore the solution of such equations should be sketched here with a small example. The equation of motion of a mass point with mass m at which a force F acts is according to Newton's second law

${\displaystyle m{\ddot {\chi }}(t)-F=0\,.}$

The location of the mass point is given by the motion function χ (t) as a function of time t and the two attached points symbolize the second time derivative (acceleration). We are looking for a solution in the time interval [0,1]. With constant force, this Dgl can be integrated closed:

${\displaystyle {\ddot {\chi }}(t)={\frac {F}{m}}\quad \rightarrow \;{\dot {\chi }}(t)=v_{0}+{\frac {F}{m}}t\quad \rightarrow \;\chi (t)=X+v_{0}t+{\frac {F}{2m}}t^{2}\,.}$

In addition to the function χ (t), the mass m and the time t, this solution contains three variables: X, v ₀ and F, which have to be specified in a concrete calculation case. The conditions prevailing at the start of the movement are the initial conditions , which are determined here by the position X and speed v ₀ at time t = 0. The force F is one of the boundary conditions that are generally dependent on time and place .

The functions χ _h (t), which at time t = 0, the homogeneous initial and boundary conditions

${\displaystyle \chi _{h}(0)=0\quad \wedge \quad {\dot {\chi }}_{h}(0)=0}$

suffice, can be added in any way to a given solution of the Dgl without violating these initial and boundary conditions. In this example, the force would be constant

${\displaystyle \chi _{h}(t)={\frac {t^{2}}{2}}\quad \rightarrow \quad \chi _{h}(0)={\dot {\chi }}_{h}(0)=0\,,\quad {\ddot {\chi }}_{h}(t)=1\,.}$

The particular solution χ _p (t), however, satisfies the inhomogeneous initial and boundary conditions

${\displaystyle \chi _{p}(0)=X\quad \wedge \quad {\dot {\chi }}_{p}(0)=v_{0}\quad \rightarrow \quad \chi _{p}(t)=X+v_{0}t\,.}$

The complete solution of the Dgl is the sum of the particulate solution and the homogeneous proportions of the solution:

${\displaystyle \chi (t)=\chi _{p}(t)+{\frac {F}{m}}\chi _{h}(t)=X+v_{0}t+{\frac {F}{2m}}t^{2}\,.}$

The displacement of the body is the difference between its current position χ (t) and its starting position X and is therefore the time-dependent part of the solution function

${\displaystyle u(t)=\chi (t)-X=v_{0}t+{\frac {F}{2m}}t^{2}\,,}$

whereas the starting position X = χ (t) -u (t) is the time-independent part of the solution function. In the approximate solution of a Dgl using the method of weighted residuals ( Ritz's variation method ), a functional approach is made for the solution sought, with which the exact solution can be approximated, e.g. B .:

${\displaystyle \chi ^{h}(t)=At^{2}\quad \rightarrow \quad {\dot {\chi }}^{h}(t)=2At\quad \rightarrow \quad {\ddot {\chi }}^{h}(t)=2A\,.}$

This approach is used in the Dgl, which is usually not met exactly. The rest is the residual

${\displaystyle R(t)=m{\ddot {\chi }}^{h}(t)-F=2mA-F\,.}$

The factor A is calculated according to the Galerkin approach by multiplying the residue by the approach function, integrating it over the interval of interest, here [0.1], and making this weighted remainder disappear:

${\displaystyle \int _{0}^{1}t^{2}(2mA-F)\,\mathrm {d} t=(2mA-F)\left[{\frac {t^{3}}{3}}\right]_{0}^{1}={\frac {1}{3}}(2mA-F){\stackrel {\displaystyle !}{=}}0\quad \rightarrow \quad A={\frac {F}{2m}}\,,}$

This creates the homogeneous approximate solution

${\displaystyle \chi _{h}(t)={\frac {F}{2m}}t^{2}}$

This has to be supplemented by the particulate components in order to take into account the initial and boundary conditions:

${\displaystyle \chi (t)=\chi _{p}(t)+{\frac {F}{2m}}t^{2}=X+v_{0}t+{\frac {F}{2m}}t^{2}\,.}$

The finite element method

In the classic Ritz approach, the solution function is replaced by a sum of functions that depend on a parameter vector and can approximate every function allowed for comparison. The solution to the Dgl is thus reduced from the search for a function to the search for a parameter vector.

The initial positions of the particles - the geometry of the body - is, as stated, a particulate solution component of the Dgl that obeys the initial conditions. Simplifications result from the following assumptions of the FEM that go beyond the Ritz method and the Galerkin approach:

1. Since finding the particular solution is difficult in most cases, this, like the solution function, is also developed in sums of functions. The parameters of the approach functions are to be chosen so that the initial and boundary conditions (body geometry, initial speed) are satisfied.
2. The time and location dependency of the batch functions is divided into purely location-dependent functions and only time-dependent parameters.

In the engineer’s approach, physically significant quantities such as the coordinates or displacements of certain points are selected as parameters. This makes it easy to determine the parameters and to check their plausibility.

Standard formulation

The first application of FEM was the linear treatment of solids and structures and it was based on this that FEM received its impulses. When computing problems in solid mechanics , displacements are sought that reflect the translation, rotation and deformation of a body. During the development of the FEM, a large number of possibilities for describing the geometry and the displacements were shown. The standard formulation is the displacement method in which the displacements at selected points, the nodes , are selected as parameters and the displacements between the nodes are interpolated with shape functions .

The so-called mixed methods use not only the knot displacements but also other unknowns that physically correspond to a pressure , tension or strain . The element shifts then result from the interaction of all these variables. The isoparametric elements establish the connection between the element displacements and the node displacements directly. In addition to the advantages mentioned above, the isoparametric elements also have the additional advantage that the displacement field can be easily visualized.

Displacement method

In the important and descriptive application of the displacement method in solid mechanics, the motion function of a body is sought for all its particles as a function of time. Instead of the entire body, any part of the body can be considered at this point, and so any finite element that models a part of the body can be assumed to be a body. This should also happen in the following. The assembly of the body from finite elements is briefly discussed at the end.

Local element coordinates

For the mathematical description of each particle P is uniquely by a reference configuration a coordinate vector assigned, allowing each particle with its coordinate vector to identify: . For simplicity, each element defines its own reference configuration, which is why there local coordinates to be named, as they are based in the considered finite element. Usually, depending on the dimension d of the element. The coordinates are largely arbitrary and generally differ from the spatial coordinates of the particle. ${\displaystyle {\vec {\Theta }}\in V_{R}\subset \mathbb {R} ^{3}}$ ${\displaystyle P=P({\vec {\Theta }})\leftrightarrow {\vec {\Theta }}={\vec {\Theta }}(P)}$ ${\displaystyle {\vec {\Theta }}}$ ${\displaystyle V_{R}=[-1,1]^{d}}$ ${\displaystyle {\vec {\Theta }}}$

Movement function

The motion function that fulfills the Dgl and the initial and boundary conditions is now sought for all particles in the element . The position vector corresponds to the spatial position of the particle at time t, so that the motion function describes the path of the particle when the particle is held. ${\displaystyle {\vec {\chi }}}$ ${\displaystyle {\vec {\chi }}({\vec {\Theta }},t)}$ ${\displaystyle {\vec {\Theta }}}$ ${\displaystyle {\vec {\Theta }}}$

A finite amount of particles is required for the application of the FEM

${\displaystyle M=\lbrace {\vec {\Theta }}_{i}\in V_{R},i=1,2,...,n\rbrace }$

selected whose elements are called nodes and which span the element. Let the nodes that serve to describe the geometry be elements of the set and have numbers from the index set and those nodes that are used to describe the displacements are elements of the set with numbers from the index set . ${\displaystyle M_{x}\subseteq M}$ ${\displaystyle I_{x}\subseteq \{1,\ldots ,n\}}$ ${\displaystyle M_{u}\subseteq M}$ ${\displaystyle I_{u}\subseteq \{1,\ldots ,n\}}$

Geometric description of the body

Fig. 1: Piece by piece linear shape function (blue) in the plane

Fig. 2: Semicircle and its FE model

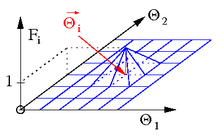
The shape of the element in the time-independent initial configuration at the beginning of the movement at the time represents - as explained above - an initial condition. The geometric position vector indicates the spatial position of the particle at the time and is therefore an object of our perception. The position vector of each particle is a sum of continuous shape functions ${\displaystyle {\vec {\chi }}_{0}({\vec {\Theta }}):={\vec {\chi }}({\vec {\Theta }},t_{0})}$ ${\displaystyle t_{0}}$ ${\displaystyle {\vec {\chi }}_{0}({\vec {\Theta }})}$ ${\displaystyle {\vec {\Theta }}}$ ${\displaystyle t_{0}}$ ${\displaystyle {\vec {\chi }}_{0}({\vec {\Theta }})}$

${\displaystyle {\vec {\chi }}_{0}({\vec {\Theta }})=\sum _{i\in I_{x}}F_{i}({\vec {\Theta }}){\vec {X}}_{i}}$

where F _{i is} the shape function and the coordinate vector of the i-th node. The functions return the value one for exactly one node and the value zero for all other nodes ${\displaystyle {\vec {X}}_{i}={\vec {\chi }}_{0}({\vec {\Theta }}_{i})}$ ${\displaystyle F_{i}({\vec {\Theta }})}$ ${\displaystyle {\vec {\Theta }}_{i}\in M_{x}}$

${\displaystyle F_{i}({\vec {\Theta }}_{j})=\left\{{\begin{array}{ll}1&\mathrm {falls} \;i,j\in I_{x}\;\mathrm {und} \;i=j\\[1ex]0&\mathrm {falls} \;i,j\in I_{x}\;\mathrm {und} \;i\neq j\end{array}}\right.\,,}$

see Fig. 1. The positions of the nodes in are reproduced exactly with the shape functions ${\displaystyle M_{x}}$

${\displaystyle {\vec {\chi }}_{0}({\vec {{\Theta }_{j}}})=\sum _{i\in I_{x}}F_{i}({\vec {\Theta }}_{j}){\vec {X}}_{i}=F_{j}({\vec {\Theta }}_{j}){\vec {X}}_{j}={\vec {X}}_{j}\quad \forall \;j\in I_{x}}$

and the positions of the particles between the nodes are interpolated with the shape functions, which is the name given to these functions. If the course of the shape functions between the nodes does not correspond to the shape of the body, then the (inevitable in the absence of an analytical solution) discretization error occurs , see Fig. 2.

Displacement field

Fig. 3: Iso-, sub- and superparametric elements

The difference vector

${\displaystyle {\vec {u}}({\vec {\Theta }},t)={\vec {\chi }}({\vec {\Theta }},t)-{\vec {\chi }}_{0}({\vec {\Theta }})}$

between the momentary position of a particle and its starting position is the displacement vector, which is the time-dependent part of the motion function and which is developed into a sum of products of continuous, purely position-dependent approach functions and purely time-dependent node variables:

${\displaystyle {\vec {u}}({\vec {\Theta }},t)=\sum _{i\in I_{u}}H_{i}({\vec {\Theta }}){\vec {u}}_{i}(t)\,.}$

The shape functions H _i return the value one for exactly one node and the value zero for all other nodes: ${\displaystyle {\vec {\Theta }}_{i}\in M_{u}}$

${\displaystyle H_{i}({\vec {\Theta }}_{j})=\left\{{\begin{array}{ll}1&\mathrm {falls} \;i,j\in I_{u}\;\mathrm {und} \;i=j\\[1ex]0&\mathrm {falls} \;i,j\in I_{u}\;\mathrm {und} \;i\neq j\end{array}}\right.\,.}$

The parameter vector contains the generally time-dependent displacements of the node i. More ( ) or fewer ( ) nodes can be used than are used to describe the starting position, which the sub- or superparametric elements also do, see Fig. 3. ${\displaystyle {\vec {u}}_{i}(t)}$ ${\displaystyle M_{x}\subset M_{u}}$ ${\displaystyle M_{u}\subset M_{x}}$

Constant displacement field

With these two approaches, the motion function is:

${\displaystyle {\vec {\chi }}({\vec {\Theta }},t)={\vec {\chi }}_{0}({\vec {\Theta }})+{\vec {u}}({\vec {\Theta }},t)=\sum _{i\in I_{x}}F_{i}({\vec {\Theta }}){\vec {X}}_{i}+\sum _{i\in I_{u}}H_{i}({\vec {\Theta }}){\vec {u}}_{i}(t)\,.}$

In order to make physical sense, the approach functions must be able to represent a parallel displacement of the body. In the case of a parallel shift , all particles and thus also all nodes of the model are shifted with the vector regardless of their location . Then the displacement field is ${\displaystyle {\vec {u}}_{0}}$

${\displaystyle {\vec {u}}({\vec {\Theta }},t)=\sum _{i\in I_{u}}H_{i}({\vec {\Theta }}){\hat {u}}_{0}=\left(\sum _{i\in I_{u}}H_{i}({\vec {\Theta }})\right){\hat {u}}_{0}{\stackrel {\displaystyle !}{=}}{\vec {u}}_{0}\quad \forall \;{\vec {\Theta }}\in V_{R}\,,}$

why

${\displaystyle \displaystyle \sum _{i\in I_{u}}H_{i}({\vec {\Theta }})=1\quad \forall \;{\vec {\Theta }}\in V_{R}}$		(I)

is to be demanded. It is also required that the displaced body can also be displayed with a displaced starting position:

${\displaystyle {\begin{array}{rcl}{\vec {\chi }}_{0}({\vec {\Theta }})+{\vec {u}}_{0}&=&\displaystyle \sum _{i\in I_{x}}F_{i}({\vec {\Theta }}){\vec {X}}_{i}+\sum _{i\in I_{u}}H_{i}({\vec {\Theta }}){\hat {u}}_{0}{\stackrel {\displaystyle !}{=}}\sum _{i\in I_{x}}F_{i}({\vec {\Theta }})({\vec {X}}_{i}+{\hat {u}}_{0})\\\rightarrow \displaystyle \sum _{i\in I_{x}}F_{i}({\vec {\Theta }}){\hat {u}}_{0}&=&\displaystyle \left(\sum _{i\in I_{x}}F_{i}({\vec {\Theta }})\right){\hat {u}}_{0}=\sum _{i\in I_{u}}H_{i}({\vec {\Theta }}){\hat {u}}_{0}\,.\end{array}}}$

Because of condition (I) it follows:

${\displaystyle \displaystyle \sum _{i\in I_{x}}F_{i}({\vec {\Theta }})=1\quad \forall \;{\vec {\Theta }}\in V_{R}\,.}$		(II)

Isoparametric elements

The first characteristic of isoparametric elements to be noticed is that the same nodes are used to represent the displacement as for the geometry:

${\displaystyle M_{u}=M_{x}=M\,.}$

The second property of isoparametric elements is that the same continuous shape functions are used for the representation of the displacement as for the starting position

${\displaystyle {\vec {\chi }}({\vec {\Theta }},t)=\sum _{i=1}^{n}N_{i}({\vec {\Theta }}){\vec {X}}_{i}+\sum _{i=1}^{n}N_{i}({\vec {\Theta }}){\vec {u}}_{i}(t)=\sum _{i=1}^{n}N_{i}({\vec {\Theta }})({\vec {X}}_{i}+{\vec {u}}_{i}(t))\,.}$

Following the Galerkin approach , the same functions are used for the weighting functions as for the geometry and displacement. These properties mean that

1. the shape functions only need to fulfill requirement (I), since then (II) is automatically fulfilled,
2. the discretization error can be easily assessed visually in the preprocessor and
3. only one set of shape functions needs to be defined and programmed for the geometry, the displacements and the weighting functions.

Whole body modeling

The movement function must be continuous in the element and this is also required for the global movement function of the entire solid. Usually, it is specified that the local movement function defined in the element disappears outside the element and the global movement function is the sum of all local element movement functions. In order for the global movement function to be constant, neighboring elements must be compatible so that they build up the body without overlapping and without gaps. This means that neighboring elements on their common boundary surface have the same nodes and the same course of the shape functions, see Fig. 2 and 3.

example

A one-dimensional bar element

A one-dimensional isoparametric rod element has the local coordinate

${\displaystyle \Theta \in [-1,1]}$

along its axis, s. Image. With the shape functions

${\displaystyle f_{1}(\Theta )={\frac {1}{2}}(1-\Theta )}$

${\displaystyle f_{2}(\Theta )={\frac {1}{2}}(1+\Theta )}$

each point can be represented on its axis:

${\displaystyle {\vec {X}}=f_{1}(\Theta ){\vec {X}}_{1}+f_{2}(\Theta ){\vec {X}}_{2}={\frac {1}{2}}(1-\Theta ){\vec {X}}_{1}+{\frac {1}{2}}(1+\Theta ){\vec {X}}_{2}\,.}$

The requirement (I) for the shape functions is fulfilled in this element:

${\displaystyle 1{\stackrel {\displaystyle !}{=}}f_{1}(\Theta )+f_{2}(\Theta )={\frac {1}{2}}(1-\Theta )+{\frac {1}{2}}(1+\Theta )=1\,.}$

The element can thus describe a translation in space.

Footnotes

1. ↑ ^{a b} Schwarz [1980], p. 37ff
2. ↑ KJ Bathe, p. 395

literature

• Klaus-Jürgen Bathe: Finite Element Methods: Matrices and linear algebra, the finite element method, solving equilibrium conditions and equations of motion . Springer 1986, ISBN 3-540-15602-X .
• Klaus Knothe, Heribert Wessels: Finite elements: an introduction for engineers . Springer, 2008. ISBN 3-540-72188-6 .
• HR Schwarz: Finite Element Method . Teubner, Stuttgart 1980.
• Peter Wriggers: Nonlinear Finite Element Methods . Springer, 2001. ISBN 3-540-67747-X .