Static determinacy
The Static definiteness is a property of static mechanical systems with one hand and on the other hand theoretical practical importance.
- Theoretical meaning: The system is in mechanical equilibrium in such a way that precisely the external forces and moments (including those occurring at the bearing points) the equilibrium conditions (sum of all forces in each of the 3 spatial directions and sum of all moments around each of the 3 spatial axes equal zero ) fulfill. The i. d. Usually the task at hand, the forces and moments on the bearings ( bearing reactions ) of z. B. Determining structures can be solved with the help of these 6 equations (3 in the flat case).
- Practical meaning: Statically determined systems such as B. Structures
- can be assembled from their rigid components and stored without constraints (prior deformation of individual components);
- experience no constraints (deformation of individual components) or freedom of movement (wobbly) due to thermal expansion of the components or dislocations of the bearing foundations .
A distinction is made between static underdetermination (point 2. does not apply) and static overdetermination (also referred to as static indeterminacy , point 1. does not apply).
Three different values of the degree of freedom f are assigned to these three individual terms :
- static underdetermination: f = ≥1,
- static determination: f = 0,
- static overdetermination or indeterminacy: f ≤-1.
Structures that are statically under-determined (f = ≥1) are of no practical importance, since they would collapse due to their possibility of movement (on the other hand, gears require one or more movement possibilities, here called degree of movement F ≥ 1).
Structures designed statically over / indefinitely (f ≤-1) are practically relevant as well as statically determined (f = 0). The static determinacy enables the simple and easy-to-understand, safe design of the supporting structure through the evaluation of the sufficient number of existing equilibria of forces and moments. Designing statically indeterminate structures has been possible since the development of elastostatics and is now easily and reliably possible with the help of a computer - unfortunately at the expense of clarity. This is because statically indeterminate does not necessarily mean that unacceptable deformations occur in particular during operation. To strive for static determinacy the longer the more a "theoretical luxury" with u. U. significant surcharge. So only because of the static determinacy z. For example, no joints in bridge girders are justifiable "... if this arrangement of joints does not result in any advantages" or if the deformations during use are insignificant and therefore bearable.
Relationships between reactions and movement possibilities
- A structure is statically determined when every possibility of rigid body movement is prevented by a bearing or connection reaction. That is, if a system is statically determined, then the number of support and connection reactions is equal to the number of possible rigid body movements. Conversely, however, it does not necessarily follow that a structure is statically determined if the number of support and connection reactions is equal to the number of possible rigid body movement possibilities (it is therefore only a sufficient condition for static determination). To determine the support reactions and the internal forces , the equilibrium conditions are sufficient for statically determined systems in the theory of the first order .
- A structure is statically indeterminate (or statically overdetermined) if the number of support and connection reactions exceeds the number of possible rigid body movements. More than one reaction counteracts at least one possibility of rigid body movement. The determination of the reaction values is generally only possible taking into account the deformation properties of the elements of such structures ( second order theory ).
- A structure is statically underdetermined if at least one rigid body movement is not counteracted by any reaction, i.e. H. if the body can move in the sense of a rigid body (infinitesimal): freely move or rotate or internal displacements of a kinematic chain. If the number of support and connection reactions is smaller than the number of possible rigid body movements, a structure is statically underdetermined, but a static underdetermination does not necessarily mean that the number of support and connection reactions is smaller than the number of possible rigid bodies -Motion possibilities, since in the counting formula (see below) a multiple static over-determination can cancel out a static under-determination. Therefore, other methods than the counting formula, such as the build-up / breakdown criterion or from perception, are more reliable.
Degree of static indeterminacy
The degree of static indeterminacy is specified in structural engineering with the integer value:
- n-fold statically indeterminate (statically overdetermined),
- i. d. Usually statically determined,
- Can be moved n-times (statically under-determined).
Construction / dismantling criterion
For the construction criterion, it is expedient to start from a statically determined basic system and to get the desired system by adding / removing binding values / storage reactions. Here you usually start with one
- Beam on two supports
- a cantilever
- A three-hinge frame
- a triangular framework made of three hinged rods
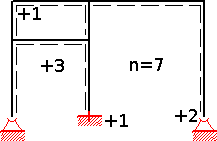
Example: The degree of static uncertainty is sought in a system. A (similar) statically determined basic system is selected and then statically determined cantilever arms are added. You add bonds and support reactions (or remove them in the case of kinematic systems) and add their value.
General counting criterion
The determination of n can be done with the following formula, known as the counting criterion :
- level structures:
- spatial structures:
Here are:
- : Number of possible support forces ( values of the supports)
- : Number of possible intermediate forces ( valences of the connections),
- : Number of rigid components / beams.
by forming you also get the following alternative formula:
With
- : Number of possible support forces ( values of the supports)
- : Number of sections of the continuous beam between the points counted for
- : Number of nodes / member ends
- : Number of relative movements between the connected members that are not prevented
Sample calculation: (flat) rigid body Gerber beam
- ⇐ the Gerber girder is a statically determined structure.
The counting criterion is a necessary but not a sufficient condition. In this process, under- and over-determination can cancel each other out. An example of this is a two-part beam that rests on three floating bearings: Despite the determined n = 0, it is obviously not statically determined. Therefore, z. B. to make a statement about the displaceability of the structure with the kinematics through a pole plan.
Counting criterion for level trusses
A simplified counting criterion can be used for level ideal trusses , since all bars are hinged on both sides:
Here are:
- : Sum of the movement possibilities prevented in the support swivel joints ( values of the supports)
- : Number of bars
- : Number of swivel joints (supports + connections).
This counting criterion results from the fact that only swivel joints occur (or are assessed as such) in the supports and connections of trusses.
Example: truss shown on the right
- ⇐ the framework shown opposite is statically determined.
The counting criterion for trusses is also only a necessary, but not sufficient, condition for the verification of static determinacy.
Equilibrium conditions
All statically determined systems can be calculated with the equilibrium conditions , including equivalence conditions.
Flat system

In a rigid planar system, the degree of freedom = 3: two translational movement possibilities and one rotational movement possibility. To obtain a particular system of equations, three equations are therefore necessary. Each of these three equations deals with a possibility of movement. The sums of the horizontal forces, vertical forces and moments for a specified reference point A must be 0 in an equilibrium system:
The equivalence theorem for general systems of forces , which is based on the reduction to dynames , states that for the equilibrium conditions, equations of forces may be replaced by equations of moments. Possible equilibrium conditions in the plane are therefore:
With this approach, however, any linear dependencies that may occur must be taken into account. If, for example, only moment equations are used and all reference points are on a straight line, there is no valid equivalence condition.
In a central system of forces , i.e. a system of forces in which the lines of action of all forces intersect at one point, no moments occur, so that only two equations are required here:
Spatial system
There are three translational and three rotational movement possibilities in space, so the equilibrium condition consists of six equations: Three equations deal with the force in each of the three coordinate directions, three further equations deal with the moment in each of the three coordinate directions:
It is also possible in space to replace one or more equations of forces with equations of moments.
Internal forces due to constraint
In statically determined systems, deformations caused by displacements and rotations of the bearings, thermal expansion, creep and shrinkage of concrete i. A. No internal forces, but internal stresses can occur. Deformations can, for. B. misalignment of supports are caused, which i. d. Usually leads to a change in the cutting size.
Especially in the Composite residual stresses may i due deformations. A. not be neglected even in statically determined systems, one then speaks of primary constrained stresses , which (without external load) lead to secondary constrained stresses in statically overdetermined systems .
In statically indeterminate systems, the above Actions i. A. Internal sizes.
When calculating static (or dynamic) systems, restraint stresses are i. A. to be considered.
Internal and external static determinacy
In a series of bar structures, it is appropriate and descriptive to distinguish between internal and external static certainty:
- a system is said to be internally statically determined if the internal forces on intersected subsystems can be calculated from the load using the equilibrium conditions;
- A system or system part is called externally statically determined if the external bearing reactions can be calculated from the load using the equilibrium conditions alone.
Examples

Statically determined systems are for example:
-
Single-span beam (beam on two supports)
- Single-span beam with cantilever arm
- Cantilever
- Three-hinge frame
- Three-hinged arch
- Tannery
Statically indeterminate systems are for example:
Examples of an externally determined but internally indeterminate system:
- Framework truss.
literature
- N. Hinrichs: Don't panic about mechanics! Springer, 2009, ISBN 978-3-8348-0646-8 ( limited preview in Google book search).
- C. Spura: Technical Mechanics 1. Stereostatics . Springer, 2016, ISBN 978-3-658-14984-0 .
- Karl-Eugen Kurrer : History of Structural Analysis. In search of balance , Ernst and Son, Berlin 2016, p. 32ff, ISBN 978-3-433-03134-6 .
Remarks
- ↑ z. B. a beam on two supports, in which you insert a joint in the middle
Individual evidence
- ^ Fritz Stüssi: Structural Analysis I , Birkhäuser 1971, page 115.
- ↑ a b c K. Meskouris, E. Hake: Statics of the rod support structures: Introduction to structural engineering . Springer, 1999, ISBN 978-3-540-66136-8 , pp. 44 f . ( limited preview in Google Book search).
- ↑ Oliver Romberg, Nikolaus Hinrichs: Don't panic about mechanics! - Success and fun in the classic "loser subject" of engineering studies . In: Study without panic . 8th, revised edition. tape 4 . Vieweg + Teubner Verlag, 2011, ISBN 978-3-8348-1489-0 , doi : 10.1007 / 978-3-8348-8174-8 (349 pages, first edition: 1999).
- ↑ B. Kauschinger, St. Ihlenfeldt: 6. Kinematics. (No longer available online.) Archived from the original on December 27, 2016 ; accessed on December 27, 2016 . Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ Jürgen Fröschl, Florian Achatz, Steffen Rödling, Matthias Decker: Innovative component test concept for crankshafts . In: MTZ-Motortechnische Zeitschrift . tape 71 , no. 9 . Springer, 2010, p. 614-619 , doi : 10.1007 / BF03225605 .
- ↑ At n = 0 there can be an x-fold static overdetermination and at the same time an x-fold static underdetermination, which is not canceled out in the formula, however, in the mechanical properties. With x ∈ ℕ .
- ↑ Tobias Nef, Gery Colombo, Robert Riener: ARMin - robot for movement therapy of the upper extremities . In: Automation technology . tape 53 , no. 12 , 2005.
- ^ Wilhelm Schröder: Fine positioning with ball screws . No. 11907 . Diss. Techn. Wiss. ETH Zurich, 1996, doi : 10.3929 / ethz-a-001702546 ( ethz.ch [PDF]).
- ↑ Dieter Dinkler: Basics of structural engineering, models and calculation methods for level bar structures . Springer, March 20, 2012, Fundamentals of the calculation methods, p. 31-64 , doi : 10.1007 / 978-3-8348-2372-4_3 .
- ^ Bernhard Pichler, Josef Eberhardsteiner : Structural Analysis VO - LVA no. 202.065 . Ed .: E202 Institute for Mechanics of Materials and Structures - Faculty of Civil Engineering, TU Vienna. SS 2016 edition. TU Verlag, Vienna 2016, ISBN 978-3-903024-17-5 , angle of rotation method (520 pages, tuverlag.at - first edition: 2012). Structural analysis VO - LVA no. 202.065 ( Memento of the original from March 13, 2016 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ Roman Harcke: Static determinateness of counting criterion
- ↑ a b c d e Bernd Markert : Mechanics 1 Stereostatics. Statics of rigid bodies. Institute for General Mechanics , Aachen 2014.
- ↑ Oliver Romberg, Nikolaus Hinrichs: Don't panic about mechanics. Vieweg & Teubner Verlag, Wiesbaden 2011, ISBN 978-3-8348-1489-0 , p. 35.
- ↑ Learn statics. Basics. Archived from the original on August 27, 2016 ; accessed on October 14, 2017 .
- ↑ B. Marussig: Force size method , page 6: Disadvantages of the counting criterion
- ↑ statik-lernen.de: Static (in) certainty counting criterion
- ↑ Marussig, Kraft size method , page 5, example d: Counting criterion not sufficient