Theorem of Betti

The Betti's theorem (also set by Maxwell and Betti , Reziprozitätsatz Betti or set of reciprocal displacement of the work ) was 1872 by Enrico Betti formulated. It says that in two equal, linear elastic systems, which are deformed by forces , in equilibrium

"The work that the forces of the first system do on the paths of the second system are the same as the work that the forces of the second system do on the paths of the first system."

- Wolfram Franke, Thorsten Kunow :

The work of one system of forces on the displacements caused by another system of forces is called reciprocal work . The sentence also applies to torques that work on twisting, as well as for mechanical stresses that work on elongation , which is also the proof of this. Instead of loading two systems of the same kind at the same time, one system can be loaded with two systems of forces one after the other .

Betti's theorem has meaning in technical mechanics , especially in structural engineering . It is also a basis of the boundary element method .

Continuum mechanics

A linear elastic body is given, which has the volume V and the surface A, and which is loaded with surface forces and volume-distributed forces (for example gravity ). The set of displacement, strain tensor and stress tensor fields is an elastic state of the body that belongs to the external force system if ${\displaystyle {\vec {s}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle \{{\vec {u}},{\boldsymbol {\varepsilon }},{\boldsymbol {\sigma }}\}}$ ${\displaystyle \{{\vec {s}},{\vec {b}}\}}$

${\displaystyle \int _{A}{\vec {s}}\cdot {\vec {u}}\,\mathrm {d} A+\int _{V}{\vec {b}}\cdot {\vec {u}}\,\mathrm {d} V=\int _{V}{\boldsymbol {\sigma }}:{\boldsymbol {\varepsilon }}\,\mathrm {d} V}$

applies, see Clapeyron's theorem . The arithmetic symbol " " is the scalar product of vectors and the colon ":" forms the Frobenius scalar product of two tensors A and B using the trace A  : B  : = Sp ( A ^T · B ). The work done by the external forces and on the displacements is therefore equal to the work of deformation of the stresses σ at the distortions ε . ${\displaystyle \cdot }$ ${\displaystyle {\vec {s}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {u}}}$

The shifts are related to the distortions. Here grad forms the gradient and the superscript T stands for the transposition . The stress tensor σ results from the strain tensor ε using a symmetrical elasticity tensor : ${\displaystyle {\boldsymbol {\varepsilon }}={\tfrac {1}{2}}(\operatorname {grad} ({\vec {u}})+\operatorname {grad} ({\vec {u}})^{\top })}$

${\displaystyle \mathbb {C} =\mathbb {C} ^{\top }\quad \rightarrow \quad {\boldsymbol {\sigma }}:=\mathbb {C} :{\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}:\mathbb {C} }$

With the product “:” a fourth order tensor ( ) maps a second order tensor ( ε ) to a second order tensor ( σ ). In Hooke's law, would be isotropy ${\displaystyle \mathbb {C} }$

${\displaystyle \mathbb {C} =2\mu \mathbb {I} +\lambda \mathbf {1\otimes 1} \quad \rightarrow \quad {\boldsymbol {\sigma }}=\mathbb {C} :{\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}:\mathbb {C} =2\mu {\boldsymbol {\varepsilon }}+\lambda \operatorname {Sp} ({\boldsymbol {\varepsilon }})\mathbf {1} }$

The material parameters are the Lamé constants , the unit tensors of the second or fourth order and both are symmetrical. Therefore also applies and . Isotropy is not required in Betti's theorem and the elasticity tensor may be position-dependent. ${\displaystyle \{\mu ,\lambda \}}$ ${\displaystyle \{\mathbf {1} ,\mathbb {I} \}}$ ${\displaystyle \mathbf {1} :{\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}:\mathbf {1} =\operatorname {Sp} ({\boldsymbol {\varepsilon }})}$ ${\displaystyle \mathbb {I} :{\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}:\mathbb {I} ={\boldsymbol {\varepsilon }}}$

Now be a second elastic state of the body that belongs to the external system of forces . Then Betti's sentence says: ${\displaystyle \{{\vec {\tilde {u}}},{\tilde {\boldsymbol {\varepsilon }}},{\tilde {\boldsymbol {\sigma }}}\}}$ ${\displaystyle \{{\vec {\tilde {s}}},{\vec {\tilde {b}}}\}}$

${\displaystyle \int _{A}{\vec {s}}\cdot {\vec {\tilde {u}}}\,\mathrm {d} A+\int _{V}{\vec {b}}\cdot {\vec {\tilde {u}}}\,\mathrm {d} V=\int _{V}{\boldsymbol {\sigma }}:{\tilde {\boldsymbol {\varepsilon }}}\,\mathrm {d} V=\int _{V}{\tilde {\boldsymbol {\sigma }}}:{\boldsymbol {\varepsilon }}\,\mathrm {d} V\,.=\int _{A}{\vec {\tilde {s}}}\cdot {\vec {u}}\,\mathrm {d} A+\int _{V}{\vec {\tilde {b}}}\cdot {\vec {u}}\,\mathrm {d} V}$

The symmetry of the elasticity tensor is a necessary prerequisite for this, which is given in the case of hyperelasticity . ${\displaystyle \mathbb {C} }$

proof

The Betti's theorem is a consequence of the "set of the work done" ( English theorem of work expended ) is the foremost derived.

A displacement field with an associated distortion field is given in the volume of the body . Regardless of this, there is a symmetrical stress tensor field in the same volume , which satisfies the equilibrium condition and on the surface of the body , in which the stress vector applied by forces on the surface is and the normal unit vector directed outwards on the surface of the body (and is therefore written with a hat ). Apart from the external force system , there are no other forces acting on the body. The reciprocal work of the surface tensions on the displacements is expressed with the stress tensor: ${\displaystyle {\vec {u}}}$ ${\displaystyle {\boldsymbol {\varepsilon }}={\tfrac {1}{2}}(\operatorname {grad} ({\vec {u}})+\operatorname {grad} ({\vec {u}})^{\top })}$ ${\displaystyle {\tilde {\boldsymbol {\sigma }}}}$ ${\displaystyle \operatorname {div} {\tilde {\boldsymbol {\sigma }}}+{\vec {\tilde {b}}}={\vec {0}}}$ ${\displaystyle {\vec {\tilde {s}}}={\tilde {\boldsymbol {\sigma }}}\cdot {\hat {n}}}$ ${\displaystyle {\vec {\tilde {s}}}}$ ${\displaystyle {\hat {n}}}$ ${\displaystyle \{{\vec {\tilde {s}}},{\vec {\tilde {b}}}\}}$

${\displaystyle \int _{A}{\vec {\tilde {s}}}\cdot {\vec {u}}\;\mathrm {d} A=\int _{A}({\tilde {\boldsymbol {\sigma }}}\cdot {\hat {n}})\cdot {\vec {u}}\;\mathrm {d} A=\int _{A}({\tilde {\boldsymbol {\sigma }}}\cdot {\vec {u}})\cdot {\hat {n}}\;\mathrm {d} A}$

With sufficient smoothness of the surface, this surface integral can with the divergence theorem according to ${\displaystyle \textstyle \int _{A}{\vec {v}}\cdot {\hat {n}}\,\mathrm {d} A=\int _{V}\operatorname {div} ({\vec {v}})\,\mathrm {d} V}$

${\displaystyle \int _{A}{\vec {\tilde {s}}}\cdot {\vec {u}}\;\mathrm {d} A=\int _{A}({\tilde {\boldsymbol {\sigma }}}\cdot {\vec {u}})\cdot {\hat {n}}\;\mathrm {d} A=\int _{V}\operatorname {div} ({\tilde {\boldsymbol {\sigma }}}\cdot {\vec {u}})\;\mathrm {d} V}$

be converted into a volume integral and the product rule delivers ${\displaystyle \operatorname {div} (\mathbf {T} \cdot {\vec {v}})=\operatorname {div} (\mathbf {T} )\cdot {\vec {v}}+\mathbf {T} ^{\top }:\operatorname {grad} ({\vec {v}})}$

${\displaystyle \int _{A}{\vec {\tilde {s}}}\cdot {\vec {u}}\;\mathrm {d} A=\int _{V}\operatorname {div} ({\tilde {\boldsymbol {\sigma }}}\cdot {\vec {u}})\;\mathrm {d} V=\int _{V}\operatorname {div} ({\tilde {\boldsymbol {\sigma }}})\cdot {\vec {u}}\;\mathrm {d} V+\int _{V}{\tilde {\boldsymbol {\sigma }}}:\operatorname {grad} ({\vec {u}})\;\mathrm {d} V}$

Exploitation of the equilibrium condition and the fact that in the scalar product with the symmetrical stress tensor the asymmetrical part of the displacement gradient does not contribute anything, so the following applies, finally leads to the theorem of the work done : ${\displaystyle \operatorname {div} {\tilde {\boldsymbol {\sigma }}}=-{\vec {\tilde {b}}}}$ ${\displaystyle {\tilde {\boldsymbol {\sigma }}}:\operatorname {grad} ({\vec {u}})={\tilde {\boldsymbol {\sigma }}}:{\boldsymbol {\varepsilon }}}$

${\displaystyle \int _{A}{\vec {\tilde {s}}}\cdot {\vec {u}}\;\mathrm {d} A+\int _{V}{\vec {\tilde {b}}}\cdot {\vec {u}}\;\mathrm {d} V=\int _{V}{\tilde {\boldsymbol {\sigma }}}:{\boldsymbol {\varepsilon }}\;\mathrm {d} V}$

As a prerequisite for the validity of this equation, the displacement, distortion and stress field must meet the following requirements:

• The displacement field is permitted if ${\displaystyle {\vec {u}}}$
  • it is twice differentiable in the volume V of the linear-elastic body , and
  • it is continuous like its gradient in the volume including its surface (in the closed volume) [V] . ${\displaystyle \operatorname {grad} {\vec {u}}}$
• The stress tensor field is permissible if
  • it is continuous and continuously differentiable ( smooth ) in the volume V ,
  • like its divergence in the closed volume [V] it is continuous.

In the set of work done, the field of tension and the field of distortion are independent of each other and not necessarily linked by a material model . The external forces therefore do the same work on the displacement field as the stresses induced by the external forces on the distortions belonging to the displacement field. ${\displaystyle \{{\vec {\tilde {s}}},{\vec {\tilde {b}}}\}}$ ${\displaystyle \{{\vec {\tilde {s}}},{\vec {\tilde {b}}}\}}$

For a second group of external forces with a stress field and a second displacement field with a distortion field, one can use the same method ${\displaystyle \{{\vec {s}},{\vec {b}}\}}$ ${\displaystyle {\boldsymbol {\sigma }}}$ ${\displaystyle {\vec {\tilde {u}}}}$ ${\displaystyle {\tilde {\boldsymbol {\varepsilon }}}={\tfrac {1}{2}}(\operatorname {grad} ({\vec {\tilde {u}}})+\operatorname {grad} ({\vec {\tilde {u}}})^{\top })}$

${\displaystyle \int _{A}{\vec {s}}\cdot {\vec {\tilde {u}}}\;\mathrm {d} A+\int _{V}{\vec {b}}\cdot {\vec {\tilde {u}}}\;\mathrm {d} V=\int _{V}{\boldsymbol {\sigma }}:{\tilde {\boldsymbol {\varepsilon }}}\;\mathrm {d} V}$

derive. The integral equations keep their validity if and are elastic states of the body. Then with a symmetric elasticity tensor and and it follows: ${\displaystyle \{{\vec {u}},{\boldsymbol {\varepsilon }},{\boldsymbol {\sigma }}\}}$ ${\displaystyle \{{\vec {\tilde {u}}},{\tilde {\boldsymbol {\varepsilon }}},{\tilde {\boldsymbol {\sigma }}}\}}$ ${\displaystyle {\boldsymbol {\sigma }}=\mathbb {C} :{\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}:\mathbb {C} }$ ${\displaystyle {\tilde {\boldsymbol {\sigma }}}=\mathbb {C} :{\tilde {\boldsymbol {\varepsilon }}}}$

${\displaystyle {\boldsymbol {\sigma }}:{\tilde {\boldsymbol {\varepsilon }}}=({\boldsymbol {\varepsilon }}:\mathbb {C} ):{\tilde {\boldsymbol {\varepsilon }}}={\boldsymbol {\varepsilon }}:(\mathbb {C} :{\tilde {\boldsymbol {\varepsilon }}})={\boldsymbol {\varepsilon }}:{\tilde {\boldsymbol {\sigma }}}={\tilde {\boldsymbol {\sigma }}}:{\boldsymbol {\varepsilon }}}$

From the above, Betti's theorem results:

${\displaystyle \int _{A}{\vec {s}}\cdot {\vec {\tilde {u}}}\;\mathrm {d} A+\int _{V}{\vec {b}}\cdot {\vec {\tilde {u}}}\;\mathrm {d} V=\int _{V}{\boldsymbol {\sigma }}:{\tilde {\boldsymbol {\varepsilon }}}\;\mathrm {d} V=\int _{V}{\tilde {\boldsymbol {\sigma }}}:{\boldsymbol {\varepsilon }}\;\mathrm {d} V=\int _{A}{\vec {\tilde {s}}}\cdot {\vec {u}}\;\mathrm {d} A+\int _{V}{\vec {\tilde {b}}}\cdot {\vec {u}}\;\mathrm {d} V}$

The symmetry of the elasticity tensor is a necessary prerequisite, without which the theorem does not apply. However, anisotropy and inhomogeneity of the material are permitted.

Examples

Cantilever

Cantilever to demonstrate Betti's theorem

We consider a horizontally supported beam on which points 1 and 2 are arbitrarily defined, just not in the supports (because that would be a trivial case). First we let a vertical force P act at point 1 and measure the vertical depression of point 2, which we call. Next, we remove the force P again and now put a force Q at point 2. This produces a reduction in point 1: . According to Betti: ${\displaystyle \Delta _{P2}}$ ${\displaystyle \Delta _{Q1}}$

${\displaystyle P\cdot \Delta _{Q1}=Q\cdot \Delta _{P2}.}$

Two-spring-mass system

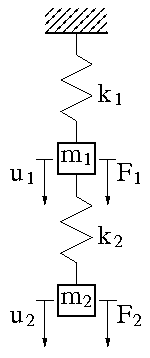
Linear two-spring-mass system.

Let two bodies be connected to each other and to the wall via two springs with stiffnesses k ₁ and k ₂ and are loaded with two forces F ₁ and F ₂ , see figure below on the right. In equilibrium, the bodies then shift according to:

${\displaystyle \underbrace {\begin{pmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}\end{pmatrix}} _{=:\mathbf {K} }{\begin{pmatrix}u_{1}\\u_{2}\end{pmatrix}}={\begin{pmatrix}F_{1}\\F_{2}\end{pmatrix}}\leftrightarrow {\begin{pmatrix}u_{1}\\u_{2}\end{pmatrix}}={\frac {1}{k_{1}k_{2}}}{\begin{pmatrix}k_{2}&k_{2}\\k_{2}&k_{1}+k_{2}\end{pmatrix}}{\begin{pmatrix}F_{1}\\F_{2}\end{pmatrix}}}$

In the first elastic system let

${\displaystyle {\vec {F}}={\begin{pmatrix}F_{1}\\0\end{pmatrix}}\rightarrow {\vec {u}}={\begin{pmatrix}u_{1}\\u_{2}\end{pmatrix}}={\frac {F_{1}}{k_{1}}}{\begin{pmatrix}1\\1\end{pmatrix}}}$

and be in the second elastic system

${\displaystyle {\vec {\tilde {F}}}={\begin{pmatrix}0\\{\tilde {F}}_{2}\end{pmatrix}}\rightarrow {\vec {\tilde {u}}}={\begin{pmatrix}{\tilde {u}}_{1}\\{\tilde {u}}_{2}\end{pmatrix}}={\frac {{\tilde {F}}_{2}}{k_{1}}}{\begin{pmatrix}1\\1+{\frac {k_{1}}{k_{2}}}\end{pmatrix}}}$

In accordance with Betti's theorem, is calculated

${\displaystyle F_{1}{\tilde {u}}_{1}={\frac {F_{1}{\tilde {F}}_{2}}{k_{1}}}={\tilde {F}}_{2}u_{2}}$

More generally calculate out and the reciprocal works ${\displaystyle {\vec {F}}=\mathbf {K} {\vec {u}}}$ ${\displaystyle {\vec {\tilde {F}}}=\mathbf {K} {\vec {\tilde {u}}}}$

${\displaystyle {\vec {F}}^{\top }{\vec {\tilde {u}}}={\vec {\tilde {u}}}^{\top }{\vec {F}}={\vec {\tilde {u}}}^{\top }\mathbf {K} {\vec {u}}={\vec {\tilde {u}}}^{\top }\mathbf {K} ^{\top }{\vec {u}}=(\mathbf {K} {\vec {\tilde {u}}})^{\top }{\vec {u}}={\vec {\tilde {F}}}^{\top }{\vec {u}}}$

The symmetry of the matrix K is necessary for matching reciprocal work .

See also

• Formula collection tensor algebra
• Tensoranalysis formula collection

Individual evidence

1. ^ Petre P. Teodorescu: Treatise on Classical Elasticity . Theory and Related Problems. Springer, Dordrecht 2013, ISBN 978-94-007-2615-4 ( google.de [accessed March 19, 2017]).
2. ^ Daniel Materna: Finite elements and influence functions, diploma thesis. (PDF) Retrieved August 25, 2016 . 
3. ↑ Wolfram Franke, Thorsten Kunow: Small basics of structural analysis . Kassel university press GmbH, Kassel 2007, ISBN 978-3-89958-306-9 ( google.de [accessed on March 5, 2017]).
4. ↑ ^{a b c d} M. E. Gurtin: The Linear Theory of Elasticity . In: S. Flügge (Ed.): Handbuch der Physik . Volume VI2 / a, Volume Editor C. Truesdell. Springer, 1972, ISBN 3-540-05535-5 , pp. 98 f .
5. ↑ Thorsten Kunow: Improved calculation of local target variables with the finite element method using basic solutions. (PDF) See chap. 2.1 , accessed August 25, 2016 . 
6. ↑ Ralf Sube: Dictionary of Physics English: German-English . Routledge, London 2001, ISBN 978-0-415-17338-4 ( google.de [accessed March 17, 2017]).

Web links

• Maxwell and Betti's theorem
• Structural mechanical investigations on a cantilever beam (pdf, 189 kB)
• Popov: The method of Castigliano II. The sentences of Betti and Maxwell. (pdf; 297 kB) TU Berlin, accessed on June 19, 2016 .