Deformation gradient

Figure 1: A body (left) and its displaced and deformed position (right). During the deformation, material lines (black) are shifted, bent and stretched

The deformation gradient (symbol:) is a means in continuum mechanics to describe the local deformation at a material point of a body. To illustrate this, one can imagine a body (in Figure 1, yellow) on which a short line (because only local changes are described, in the picture bold red) is scratched. If the body is deformed (on the right in the picture), the incised line will not only change its position in space, but will also be stretched (or compressed) and twisted. The stretching and twisting describes the deformation gradient and is a measure of the deformation, hence the name. The appendix gradient refers to the fact that local changes are described. The deformation gradient can be used to derive measures for local elongation, distortion, changes in area and volume. In the general case, the deformation gradient is dependent on both the location and the time. The change in the deformation gradient over time gives measures for the rates of change in stretching, twisting, distortion, area and volume changes. The deformation gradient is free of units. ${\displaystyle \mathbf {F} }$

Figure 2: Transformation of a vector by a tensor . ${\displaystyle {\vec {v}}}$ ${\displaystyle \mathbf {T} }$

The mentioned short lines are mathematically vectors that are transformed by the deformation gradient, the vectors generally being rotated and stretched. Illustrations of vectors are performed by tensors , see Figure 2, which is why the deformation gradient is a tensor. If it is clear to which coordinate system the deformation gradient refers, it is calculated like a Jacobian matrix and can then also be noted as a matrix . Often, the deformation gradient maps the (infinitesimally small) material line elements in the initial or reference configuration into the current or momentary configuration. In general, however, such a mapping can also take place between any other configurations to be defined.

Definition and modes of representation

definition

The movement of a material point becomes with the movement function

${\displaystyle {\vec {x}}={\vec {\chi }}({\vec {X}},t)}$

described. The vector is the current position of the material point at the moment in the current configuration. More precisely is the position of the material point in question in the undeformed initial or reference configuration of the body at a time . With a fixed material point , the movement function describes its path through space. In the Cartesian coordinate system with the standard basis { }, the point has the component representation ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle t}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle t_{0}\leq t}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}=\sum _{i=1}^{3}{x}_{i}{\vec {e}}_{i}=\sum _{i=1}^{3}{\chi }_{i}({\vec {X}},t){\vec {e}}_{i}}$

and applies accordingly . In order to investigate how the current position changes if the position varies in the undeformed starting position, the derivative is formed: ${\displaystyle {\vec {X}}=\sum _{i=1}^{3}{X}_{i}{\vec {e}}_{i}}$

${\displaystyle F_{ij}={\frac {\partial \chi _{i}({\vec {X}},t)}{\partial {X}_{j}}}}$   for    . ${\displaystyle i,j=1,2,3}$

The functions are the components of the deformation gradient with respect to the base system . ${\displaystyle F_{ij}}$ ${\displaystyle {\vec {e}}_{i}}$

To get a coordinate-free representation, the dyadic product is used: ${\displaystyle {\otimes }}$

${\displaystyle \mathbf {F} :=\mathrm {GRAD} \,{\vec {\chi }}({\vec {X}},t)={\frac {\partial \chi _{i}}{\partial X_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}={\begin{pmatrix}F_{11}&F_{12}&F_{13}\\F_{21}&F_{22}&F_{23}\\F_{31}&F_{32}&F_{33}\end{pmatrix}}_{{\vec {e}}_{i}\otimes {\vec {e}}_{j}}}$.

This is where the deformation gradient is and is the operator for the material gradient , because it is differentiated according to the material coordinates . ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathrm {GRAD} }$ ${\displaystyle {X}_{j}}$

Figure 3: Transformation of line elements through the deformation gradient

The deformation gradient can also be derived from the directional derivative

${\displaystyle \mathbf {F} ({\vec {X}},t)\cdot \mathrm {d} {\vec {X}}=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}{\vec {\chi }}{({\vec {X}}+s\;\mathrm {d} {\vec {X}},t)}\right|_{s=0}=\mathrm {d} {\vec {x}}}$

which illustrates its transformation properties of the line elements , see Figure 3. ${\displaystyle \mathrm {d} {\vec {X}}}$

Definition and value range

Figure 4: Tangent vectors (black) on material lines create tangent spaces (yellow). The gradient vectors that are dual to the tangent vectors are shown in blue. ${\displaystyle \Theta _{i}}$

Mathematically, the differential is in ${\displaystyle \mathrm {d} {\vec {X}}}$

${\displaystyle \mathrm {d} {\vec {x}}=\mathbf {F} \cdot \mathrm {d} {\vec {X}}}$

Element of the tangent space at the point of the space that the undeformed body occupies in the initial configuration (in Figure 4 above). The differential is accordingly an element of the tangential space at the point of the space that the deformed body occupies in the current configuration (in the picture below). The deformation gradient thus becomes an image ${\displaystyle \mathrm {T} _{\vec {X}}V}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle V}$ ${\displaystyle \mathrm {d} {\vec {x}}=\mathrm {d} {\vec {\chi }}}$ ${\displaystyle {\mathrm {T} }_{\vec {x}}v}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle v}$

${\displaystyle {\begin{array}{llll}\mathbf {F} {:}&\mathrm {T} _{\vec {X}}V&\mapsto &\mathrm {T} _{\vec {x}}v\\&\mathrm {d} {\vec {X}}&\rightarrow &\mathrm {d} {\vec {x}}=\mathbf {F} ({\vec {X}},t)\cdot \mathrm {d} {\vec {X}}\end{array}}}$.

Representation in convective coordinates

If convective coordinates are assigned to each material point via a reference configuration , the tangent vectors form ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {\Theta }}=(\Theta _{1},\Theta _{2},\Theta _{3})}$

${\displaystyle {\vec {G}}_{i}:={\dfrac {\partial {\vec {X}}({\vec {\Theta }})}{\partial \Theta _{i}}}}$    or.    ${\displaystyle {\vec {g}}_{i}:={\dfrac {\partial {\vec {\chi }}\left({\vec {X}}({\vec {\Theta }})\right)}{\partial \Theta _{i}}}}$

covariant bases of the tangent spaces in the point or in the point (shown in black in Figure 4). The gradients of the convective coordinates ${\displaystyle \mathrm {T} _{\vec {X}}V}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle \mathrm {T} _{\vec {x}}v}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {G}}^{i}:=\displaystyle \sum _{j=1}^{3}{\dfrac {\partial \Theta _{i}}{\partial X_{j}}}{\vec {e}}_{j}}$    or.    ${\displaystyle {\vec {g}}^{i}:=\displaystyle \sum _{j=1}^{3}{\frac {\partial \Theta _{i}}{\partial x_{j}}}{\vec {e}}_{j}}$

form contravariant bases that are dual to the covariants (shown in blue in Figure 4).

Expressed in these basic systems, the deformation gradient takes on the particularly simple form

${\displaystyle \mathbf {F} =\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\vec {G}}^{i}}$.

In this representation you can also immediately with

${\displaystyle \mathbf {F} ^{-1}=\sum _{i=1}^{3}{\vec {G}}_{i}\otimes {\vec {g}}^{i}\quad \Leftrightarrow \quad {\vec {g}}_{i}=\mathbf {F} \cdot {\vec {G}}_{i}}$.

specify the inverse of the deformation gradient. The transposed inverse deformation gradient maps the contravariant basis vectors to one another:

${\displaystyle (\mathbf {F} ^{\mathrm {T} })^{-1}=\sum _{i=1}^{3}{\vec {g}}^{i}\otimes {\vec {G}}_{i}\quad \Leftrightarrow \quad {\vec {g}}^{i}=(\mathbf {F} ^{\mathrm {T} })^{-1}\cdot {\vec {G}}^{i}}$.

The spatial deformation gradient

Usually the deformation gradient is formulated as above in its material representation. Occasionally, however, the spatial deformation gradient is also used. Because of , the deformation gradient can be inverted and the result can be expressed as a function of the spatial coordinates : ${\displaystyle \mathrm {det} (\mathbf {F} )>0}$ ${\displaystyle {\vec {X}}={\vec {\chi }}^{-1}({\vec {x}},t)}$ ${\displaystyle {\vec {x}}}$

${\displaystyle \mathbf {f} ({\vec {x}},t)=\mathbf {F} ^{-1}({\vec {\chi }}^{-1}({\vec {x}},t),t)=\operatorname {grad} ({\vec {X}},t)={\frac {\mathrm {d} ({\vec {\chi }}^{-1})_{i}}{\mathrm {d} x_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}}$.

The spatial deformation gradient then maps the line element onto the line element : ${\displaystyle \mathbf {f} ({\vec {x}},t)}$ ${\displaystyle \mathrm {d} {\vec {x}}}$ ${\displaystyle \mathrm {d} {\vec {X}}}$

${\displaystyle {\begin{array}{llll}\mathbf {f} :&\mathrm {T} _{\vec {x}}v&\mapsto &\mathrm {T} _{\vec {X}}V\\&\mathrm {d} {\vec {x}}&\rightarrow &\mathrm {d} {\vec {X}}=\mathbf {f} ({\vec {x}},t)\cdot \mathrm {d} {\vec {x}}\end{array}}}$.

Accordingly, the spatial deformation gradient has the form in convective coordinates

${\displaystyle \mathbf {f} =\sum _{i=1}^{3}{\vec {G}}_{i}\otimes {\vec {g}}^{i}}$.

Geometric linearization

→ Main article : Displacement gradient

In solid mechanics , only small deformations occur in many areas of application. In this case, the equations of continuum mechanics experience a considerable simplification through geometric linearization . For this purpose, the displacements that a material point experiences in the course of its movement are considered. Because the current position is the point that had the position in the initial configuration , the displacement is the difference ${\displaystyle {\vec {u}}({\vec {X}},t)}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {x}}={\vec {\chi }}({\vec {X}},t)}$ ${\displaystyle {\vec {X}}}$

${\displaystyle {\vec {u}}={\vec {\chi }}({\vec {X}},t)-{\vec {X}}}$.

The material gradient of the displacements is the tensor

${\displaystyle \mathbf {H} =\mathrm {GRAD} \,{\vec {u}}=\mathrm {GRAD} \,{\vec {\chi }}-\mathrm {GRAD} \,{\vec {X}}=\mathbf {F} -\mathbf {I} }$.

and is called the displacement gradient. If is a characteristic dimension of the body, then both and are required for small displacements , so that all terms that contain higher powers of or can be neglected. In this case, the following relationships arise: ${\displaystyle L_{0}}$ ${\displaystyle |{\vec {u}}|\ll L_{0}}$ ${\displaystyle \parallel \mathbf {H} \parallel \ll 1}$ ${\displaystyle {\vec {u}}}$ ${\displaystyle \mathbf {H} }$

${\displaystyle {\begin{array}{lcl}\mathbf {F} &=&\mathbf {I} +\mathbf {H} \\\mathbf {F} ^{-1}&\approx &\mathbf {I} -\mathbf {H} \\\mathrm {det} (\mathbf {F} )&\approx &1+\mathrm {Sp} (\mathbf {H} )\\\mathbf {U} &\approx &\mathbf {I} +{\frac {1}{2}}(\mathbf {H} +\mathbf {H} ^{\mathrm {T} })\\\mathbf {v} &\approx &\mathbf {I} +{\frac {1}{2}}(\mathbf {H} +\mathbf {H} ^{\mathrm {T} })\\\mathbf {R} &\approx &\mathbf {I} +{\frac {1}{2}}(\mathbf {H} -\mathbf {H} ^{\mathrm {T} })\end{array}}}$.

The tensors and occur in the polar decomposition, see below. ${\displaystyle \mathbf {U} ,\mathbf {v} }$ ${\displaystyle \mathbf {R} }$

Transformation properties

Polar decomposition

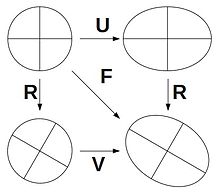
Figure 5: Polar decomposition of the deformation gradient

The deformation gradient can be clearly broken down "polar" into a rotation and a pure stretching. The representation results from the application of the polar decomposition ${\displaystyle \mathbf {F} }$

${\displaystyle \mathbf {F} =\mathbf {R\cdot U} =\mathbf {v\cdot R} }$.

Here is an "actually orthogonal tensor" . The material right stretch tensor and the spatial left stretch tensor are symmetrical and positive definite . (Donkey bridge: stands to the right of and to the left of it in the polar representation.) ${\displaystyle \mathbf {R} }$ ${\displaystyle \mathbf {U} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle \mathbf {U} }$ ${\displaystyle \mathbf {R} }$ ${\displaystyle \mathbf {v} }$

The polar decomposition clearly means a series connection of two transformations: in the one case a rotation-free stretching with subsequent rotation and in the other case a rotation with subsequent rotation-free stretching as shown in Figure 5. ${\displaystyle \mathbf {U} }$ ${\displaystyle \mathbf {R} }$ ${\displaystyle \mathbf {R} }$ ${\displaystyle \mathbf {v} }$

The right stretch tensor is calculated according to

${\displaystyle \mathbf {U} =+{\sqrt {\mathbf {F} ^{\mathrm {T} }\cdot \mathbf {F} }}}$

from the main axis transformation of , extract the root of the diagonal terms and inverse transformation, see also the example below. The same applies to the left stretch tensor ${\displaystyle \mathbf {F} ^{\mathrm {T} }\cdot \mathbf {F} }$

${\displaystyle \mathbf {v} =+{\sqrt {\mathbf {F\cdot F} ^{\mathrm {T} }}}}$.

The rotation tensor then results from ${\displaystyle \mathbf {R} }$

${\displaystyle \mathbf {R} =\mathbf {F\cdot U} ^{-1}=\mathbf {v} ^{-1}\cdot \mathbf {F} }$.

Line, area and volume elements

With the help of the deformation gradient, integrals in the material representation can be converted into the spatial one. The quantity to be integrated is a field that can be scalar, vector or tensor-valued and in the material representation and the spatial representation ${\displaystyle q}$ ${\displaystyle q_{0}({\vec {X}},t)}$

${\displaystyle q({\vec {x}},t)=q_{0}\left({\vec {\chi }}^{-1}({\vec {x}},t),t\right)}$

present. Then the identities apply:

${\displaystyle {\begin{array}{ll}\int _{l}q({\vec {x}},t)\mathrm {d} {\vec {x}}&=\int _{L}q_{0}({\vec {X}},t)\;\mathbf {F} \cdot \mathrm {d} {\vec {X}}\\\int _{a}q({\vec {x}},t){\vec {n}}\;\mathrm {d} a&=\int _{A}q_{0}({\vec {X}},t)\;\mathrm {det} (\mathbf {F} )(\mathbf {F} ^{\mathrm {T} })^{-1}\cdot {\vec {N}}\;\mathrm {d} A\\\int _{v}q({\vec {x}},t)\mathrm {d} v&=\int _{V}q_{0}({\vec {X}},t)\;\mathrm {det} (\mathbf {F} )\;\mathrm {d} V\end{array}}}$.

The operator forms the determinant and the transposed inverse . is a material line in the initial configuration and the corresponding spatial line in the current configuration. The surface of the body in the initial configuration has the surface element , i. H. the normal of the patch multiplied by the patch. The same applies to the spatial surface element on the surface of the body in the current configuration. These transformations are useful in the time derivative of the integrals on the left hand sides of the equations, because the areas on the left hand sides do not depend on time as they do on the right hand sides. ${\displaystyle \mathrm {det} (\cdot )}$ ${\displaystyle ((\cdot )^{\mathrm {T} })^{-1}}$ ${\displaystyle L}$ ${\displaystyle l}$ ${\displaystyle A}$ ${\displaystyle {\vec {N}}\mathrm {d} A}$ ${\displaystyle \mathrm {d} A}$ ${\displaystyle {\vec {N}}}$ ${\displaystyle {\vec {n}}\mathrm {d} a}$ ${\displaystyle a}$

Volume ratio

The determinant of indicates the local volume ratio in the material point under consideration during the deformation. ${\displaystyle \mathbf {F} }$ ${\displaystyle J=\mathrm {det} (\mathbf {F} )={\frac {\mathrm {d} v}{\mathrm {d} V}}>0}$

This results in u. a. that must be positive, otherwise the deformation would not be physically possible ( inversion of the material point ). ${\displaystyle J=\mathrm {det} (\mathbf {F} )}$

If the volume is retained in the event of a deformation , i.e. incompressibility is present. In the case of rubber or elastomer materials , this is a common assumption in the description of continuum mechanics and is approximately the case due to the behavior of this material class. The same applies to the incompressible liquids . ${\displaystyle J=1}$

Transformation of tensors

In addition to the line, surface and volume elements, the deformation gradient also transforms tensors from the initial configuration to the current configuration. These transformations are different for covariant tensors (often strain tensors ) and contravariant tensors (often stress tensors ), e.g. B .:

${\displaystyle {\begin{array}{lcl}\mathbf {e} &=&(\mathbf {F} ^{\mathrm {T} })^{-1}\cdot \mathbf {E} \cdot \mathbf {F} ^{-1}\\\mathbf {S} &=&\mathbf {F} \cdot {\tilde {\mathbf {T} }}\cdot \mathbf {F} ^{\mathrm {T} }\end{array}}}$.

The tensor

${\displaystyle \mathbf {e} :={\tfrac {1}{2}}(\mathbf {I} -(\mathbf {F} ^{\mathrm {T} })^{-1}\cdot \mathbf {F} ^{-1})}$

is the Euler-Almansi strain tensor in the instantaneous configuration,

${\displaystyle \mathbf {E} :={\tfrac {1}{2}}({\mathbf {F} }^{\mathrm {T} }\cdot \mathbf {F} -\mathbf {I} )}$

the Green-Lagrange strain tensor in the initial configuration,

${\displaystyle \mathbf {S} :=\mathrm {det} (\mathbf {F} )\mathbf {T} }$

the weighted Cauchy stress tensor, the Cauchy stress tensor (both in the instantaneous configuration) and ${\displaystyle \mathbf {T} }$

${\displaystyle {\tilde {\mathbf {T} }}:=\det(\mathbf {F} )\mathbf {F} ^{-1}\cdot \mathbf {T} \cdot (\mathbf {F} ^{\mathrm {T} })^{-1}}$

the second Piola-Kirchhoff stress tensor in the initial configuration. The scalar product ":" of the tensors assigned to one another in this way is not changed by the transformation, e.g. B .:

${\displaystyle \mathbf {S} :\mathbf {e} =\mathbf {F} \cdot {\tilde {\mathbf {T} }}\cdot \mathbf {F} ^{\mathrm {T} }:(\mathbf {F} ^{\mathrm {T} })^{-1}\cdot \mathbf {E} \cdot \mathbf {F} ^{-1}={\tilde {\mathbf {T} }}:\mathbf {E} }$.

Multiplicative decomposition of the deformation gradient

The multiplicative decomposition of the deformation gradient is used in material theory to model the deformation of a body due to various influences. A body can become deformed because it is heated or exposed to an external force. The deformation can also depend on how quickly the temperature or force is applied. The reactions of the material can be modeled more easily if the phenomena are viewed separately from one another. One model can simulate the influence of temperature and another model the isothermal deformation caused by forces. The deformations due to one or the other phenomenon can then be brought together again. In material theory, it has become established to use an additive decomposition of the strains for small deformations and a multiplicative decomposition of the deformation gradient for large deformations.

Let a and b be two deformation components of a material. For the modeling, the deformation gradient is decomposed multiplicatively:

${\displaystyle \mathbf {F} =\mathbf {F} _{a}\cdot \mathbf {F} _{b}}$.

One model then describes the development of the proportion due to influence a and another model describes the development of the proportion due to influence b . The deformation gradients and generally do not meet the compatibility conditions, which is why there is generally no movement field from which the two components can be derived by creating a gradient. ${\displaystyle \mathbf {F} _{a}}$ ${\displaystyle \mathbf {F} _{b}}$ ${\displaystyle \mathbf {F} _{a}}$ ${\displaystyle \mathbf {F} _{b}}$

Because the deformation gradient, as explained in the previous section, transforms tensors from one configuration to the other, the multiplicative decomposition corresponds to the introduction of an intermediate configuration . The tensors of the reference configuration are transformed with the portion and those of the current configuration are transformed into the intermediate configuration. Transformation of the Green-Lagrange strain tensor from the reference configuration into the intermediate configuration yields: ${\displaystyle \mathbf {F} _{b}}$ ${\displaystyle \mathbf {F} _{a}}$

${\displaystyle {\begin{array}{lcl}{\boldsymbol {\Gamma }}&:=&(\mathbf {F} _{b}^{\mathrm {T} })^{-1}\cdot \mathbf {E} \cdot \mathbf {F} _{b}^{-1}=(\mathbf {F} _{b}^{\mathrm {T} })^{-1}\cdot {\frac {1}{2}}\left((\mathbf {F} _{a}\cdot \mathbf {F} _{b})^{\mathrm {T} }\cdot (\mathbf {F} _{a}\cdot \mathbf {F} _{b})-\mathbf {I} \right)\cdot \mathbf {F} _{b}^{-1}=:{\boldsymbol {\Gamma }}_{a}+{\boldsymbol {\Gamma }}_{b}\\{\boldsymbol {\Gamma }}_{a}&:=&{\frac {1}{2}}\left(\mathbf {F} _{a}^{\mathrm {T} }\cdot \mathbf {F} _{a}-\mathbf {I} \right)\\{\boldsymbol {\Gamma }}_{b}&:=&{\frac {1}{2}}\left(\mathbf {I} -(\mathbf {F} _{b}^{\mathrm {T} })^{-1}\cdot \mathbf {F} _{b}^{-1}\right).\end{array}}}$

The Green-Lagrange strain tensor transformed into the intermediate configuration thus breaks down into two parts:

• One part is of the Green-Lagrange type and is formed with . ${\displaystyle {\boldsymbol {\Gamma }}_{a}}$ ${\displaystyle \mathbf {F} _{a}}$
• The other part is of the Euler-Almansi type and is formed with . ${\displaystyle \mathbf {F} _{b}}$

The same when the Euler Almansi tensor applies, with is transformed to the intermediate configuration: ${\displaystyle \mathbf {e} }$ ${\displaystyle \mathbf {F} _{a}}$

${\displaystyle \mathbf {F} _{a}^{\mathrm {T} }\cdot \mathbf {e} \cdot \mathbf {F} _{a}=\mathbf {F} _{a}^{\mathrm {T} }\cdot {\frac {1}{2}}\left(\mathbf {I} -(\mathbf {F} _{a}\cdot (\mathbf {F} _{b})^{\mathrm {T} })^{-1}\cdot (\mathbf {F} _{a}\cdot \mathbf {F} _{b})^{-1}\right)\cdot \mathbf {F} _{a}={\boldsymbol {\Gamma }}_{a}+{\boldsymbol {\Gamma }}_{b}}$

In the intermediate configuration, the two phenomena can now be modeled separately with the strain tensors and . The stress tensor resulting in the model in the intermediate configuration is then transformed into the current configuration or into the reference configuration. ${\displaystyle {\boldsymbol {\Gamma }}_{a}}$ ${\displaystyle {\boldsymbol {\Gamma }}_{b}}$ ${\displaystyle \mathbf {F} _{a}}$ ${\displaystyle \mathbf {F} _{b}}$

Deformation rates

→ Main article : Velocity gradient

The material time derivative of the deformation gradient

${\displaystyle {\dot {\mathbf {F} }}:=\mathrm {GRAD} \,{\dot {\vec {\chi }}}({\vec {X}},t)={\frac {\mathrm {d} {\dot {\chi }}_{i}}{\mathrm {d} X_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}}$

is a measure of the deformation speed. It hangs over

${\displaystyle \mathbf {l} :=\mathrm {grad} \,{\vec {v}}({\vec {x}},t)={\frac {\mathrm {d} v_{i}}{\mathrm {d} x_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}=\sum _{i,j,k=1}^{3}{\frac {\mathrm {d} v_{i}}{\mathrm {d} X_{k}}}{\vec {e}}_{i}\otimes {\vec {e}}_{k}\cdot {\frac {\mathrm {d} X_{l}}{\mathrm {d} x_{j}}}{\vec {e}}_{l}\otimes {\vec {e}}_{j}={\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}}$

with the spatial velocity gradient of the spatial velocity field . In convective coordinates it reads ${\displaystyle \mathbf {l} }$ ${\displaystyle {\vec {v}}({\vec {x}},t)}$

${\displaystyle {\begin{array}{lcl}{\dot {\mathbf {F} }}&=&\displaystyle \sum _{i=1}^{3}{\dot {\vec {g}}}_{i}\otimes {\vec {G}}^{i}\\\mathbf {l} &=&\displaystyle \sum _{i=1}^{3}{\dot {\vec {g}}}_{i}\otimes {\vec {g}}^{i}=-\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\dot {\vec {g}}}^{i}.\end{array}}}$

example

Figure 6: Shear of a square (purple) into a parallelogram (red). The shear is a pure stretching (royal blue) with subsequent twist or a twist (light blue) with subsequent stretching

The calculation of the deformation gradient and its polar decomposition is demonstrated using the shear of a square.

A square with an edge length of one is deformed into a parallelogram of the same area with a base and height of one, see Figure 6. The points of the square have the coordinates in the initial configuration

${\displaystyle {\begin{pmatrix}X\\Y\end{pmatrix}}\in [0,1]^{2}\subset \mathbb {R} ^{2}}$.

Let the slope of the parallelogram be

${\displaystyle \tan(\alpha )={\frac {5}{6}}\quad \rightarrow \quad \alpha \approx 0{,}6947\,\mathrm {rad} \approx 39{,}8055^{\circ }}$.

Then the spatial coordinates of the points are given by

${\displaystyle {\begin{pmatrix}x\\y\end{pmatrix}}={\vec {\chi }}\left({\begin{pmatrix}X\\Y\end{pmatrix}},t\right)={\begin{pmatrix}X+\tan(\alpha )Y\\Y\end{pmatrix}}={\begin{pmatrix}X+{\frac {5}{6}}Y\\Y\end{pmatrix}}}$.

As usual, with and with is identified. Then you get the deformation gradient by deriving: ${\displaystyle X}$ ${\displaystyle X_{1}}$ ${\displaystyle Y}$ ${\displaystyle X_{2}}$

${\displaystyle \mathbf {F} =\sum _{i,j=1}^{2}{\frac {\partial x_{i}}{\partial X_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}={\begin{pmatrix}1&{\frac {5}{6}}\\0&1\end{pmatrix}}}$.

The directional derivative delivers about

${\displaystyle {\begin{array}{lcl}\mathbf {F} \cdot {\begin{pmatrix}\mathrm {d} X\\\mathrm {d} Y\end{pmatrix}}&=&{\dfrac {\partial }{\partial s}}{\vec {\chi }}\left.\left({\begin{pmatrix}X\\Y\end{pmatrix}}+s{\begin{pmatrix}\mathrm {d} X\\\mathrm {d} Y\end{pmatrix}},t\right)\right|_{s=0}=\left.{\dfrac {\partial }{\partial s}}{\begin{pmatrix}(X+s\mathrm {d} X)+{\frac {5}{6}}(Y+s\mathrm {d} Y)\\(Y+s\mathrm {d} Y)\end{pmatrix}}\right|_{s=0}\\[3ex]&=&{\begin{pmatrix}\mathrm {d} X+{\frac {5}{6}}\mathrm {d} Y\\\mathrm {d} Y\end{pmatrix}}={\begin{pmatrix}1&{\frac {5}{6}}\\0&1\end{pmatrix}}{\begin{pmatrix}\mathrm {d} X\\\mathrm {d} Y\end{pmatrix}}\end{array}}}$

same result. The deformation gradient is independent of location and time and has the determinant one, which confirms that the area has been preserved. The right stretch tensor is calculated from the right Cauchy-Green tensor ${\displaystyle \mathbf {U} }$

${\displaystyle \mathbf {C} =\mathbf {F} ^{\mathrm {T} }\cdot \mathbf {F} ={\begin{pmatrix}1&0\\{\frac {5}{6}}&1\end{pmatrix}}{\begin{pmatrix}1&{\frac {5}{6}}\\0&1\end{pmatrix}}={\begin{pmatrix}1&{\frac {5}{6}}\\{\frac {5}{6}}&{\frac {61}{36}}\end{pmatrix}}}$

via principal axis transformation, pulling the root of the diagonal terms and inverse transformation. For the principal axis transformation one needs the eigenvalues and vectors of . One finds: ${\displaystyle \lambda _{1,2}}$ ${\displaystyle {\vec {v}}_{1,2}}$ ${\displaystyle \mathbf {C} }$

${\displaystyle {\begin{array}{lclclcl}\lambda _{1}&=&{\dfrac {9}{4}}&,\quad &{\vec {v}}_{1}&=&{\dfrac {1}{\sqrt {13}}}{\begin{pmatrix}2\\3\end{pmatrix}}\\[3ex]\lambda _{2}&=&{\dfrac {4}{9}}&,\quad &{\vec {v}}_{2}&=&{\dfrac {1}{\sqrt {13}}}{\begin{pmatrix}3\\-2\end{pmatrix}}\end{array}}}$.

The principal axis transformation is obtained with these eigenvalues ​​and vectors

${\displaystyle {\begin{array}{lcl}\mathbf {C} &=&\displaystyle \sum _{i=1}^{2}\lambda _{i}{\vec {v}}_{i}\otimes {\vec {v}}_{i}=\left(\sum _{j=1}^{2}{\vec {v}}_{j}\otimes {\vec {e}}_{j}\right)\cdot \left(\sum _{i=1}^{2}\lambda _{i}{\vec {e}}_{i}\otimes {\vec {e}}_{i}\right)\cdot \left(\sum _{k=1}^{2}{\vec {e}}_{k}\otimes {\vec {v}}_{k}\right)\\[3ex]&=&{\dfrac {1}{\sqrt {13}}}{\begin{pmatrix}2&3\\3&-2\end{pmatrix}}{\begin{pmatrix}{\frac {9}{4}}&0\\0&{\frac {4}{9}}\end{pmatrix}}{\dfrac {1}{\sqrt {13}}}{\begin{pmatrix}2&3\\3&-2\end{pmatrix}}\end{array}}}$

and with it the right stretch tensor

${\displaystyle \mathbf {U} =+{\sqrt {\mathbf {C} }}={\frac {1}{13}}{\begin{pmatrix}2&3\\3&-2\end{pmatrix}}{\begin{pmatrix}+{\sqrt {\frac {9}{4}}}&0\\0&+{\sqrt {\frac {4}{9}}}\end{pmatrix}}{\begin{pmatrix}2&3\\3&-2\end{pmatrix}}={\frac {1}{13}}{\begin{pmatrix}12&5\\5&{\frac {97}{6}}\end{pmatrix}}}$.

With its inverse

${\displaystyle \mathbf {U} ^{-1}={\frac {1}{13}}{\begin{pmatrix}{\frac {97}{6}}&-5\\-5&12\end{pmatrix}}}$

the result is the rotation tensor

${\displaystyle \mathbf {R} =\mathbf {F\cdot U} ^{-1}={\frac {1}{13}}{\begin{pmatrix}12&5\\-5&12\end{pmatrix}}={\begin{pmatrix}\cos(\beta )&-\sin(\beta )\\\sin(\beta )&\cos(\beta )\end{pmatrix}}}$,

see rotation matrix . The rotation tensor rotates the royal blue parallelogram or light blue square in the picture around the angle

${\displaystyle \beta =\left|\arcsin \left(-{\frac {5}{13}}\right)\right|\approx 0{,}3948\,\mathrm {rad} \approx 22{,}6199^{\circ }}$.

The left stretch tensor can now be removed more easily

${\displaystyle \mathbf {v} =\mathbf {F\cdot R} ^{\mathrm {T} }={\begin{pmatrix}1&{\frac {5}{6}}\\0&1\end{pmatrix}}{\frac {1}{13}}{\begin{pmatrix}12&-5\\5&12\end{pmatrix}}={\frac {1}{13}}{\begin{pmatrix}{\frac {97}{6}}&5\\5&12\end{pmatrix}}}$

determine.

See also

Mathematics:

• Differential geometry
• Jacobian matrix

Formula collections:

• Formula collection tensor algebra
• Tensoranalysis formula collection

literature

• H. Altenbach: Continuum Mechanics . Springer 2012, ISBN 978-3-642-24118-5 .
• P. Haupt: Continuum Mechanics and Theory of Materials. Springer Verlag, 2000, ISBN 3-540-66114-X .