Dilation (geometry)

To define a dilatation: ${\displaystyle \delta (g)|g}$

In geometry, a dilation is a collineation of an affine plane or an affine space , with the property that

• each straight line is mapped onto a straight line parallel to it.

Dilations are special affinities . The following applies more precisely:

• A dilation different from the identity is either a centric stretching (with a fixed point) or a parallel displacement (without a fixed point).

affine versions of Desargues' theorem.
Above: large sentence,
below: small sentence

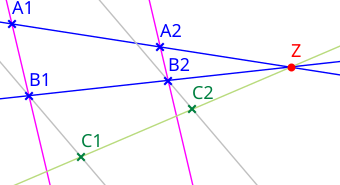
In synthetic geometry , centric elongations are also called homotheties . There they have a direct relation to the affine form of Desargues' large theorem (see picture). Parallel displacements are also called translations . They are related to the affine form of Desargues' little theorem. Performing two translations one after the other is always also a translation. The analogous statement does not apply to homotheties. For example, performing two point reflections one behind the other is a translation and not a homothety. All dilations form a groupand all translations are a subset of them. If the underlying plane / space is embedded in a projective plane / space, a dilation becomes a central collineation with the far straight line / hyperplane as the axis. More precisely: a translation or homothesis then becomes an elation or homology , depending on whether the center is on the axis or not.

In a Euclidean space one can

• a stretching at the zero point ${\displaystyle \ {\vec {x}}\to c{\vec {x}}\ ,\ c\neq 0,}$
• a translation by ${\displaystyle \ {\vec {x}}\to {\vec {x}}+{\vec {v}}\ }$

describe. While translations leave line lengths invariant, a centric stretch lengthens or shortens lines by the same factor. In the upper figure of the second picture, the blue triangle is mapped onto the green triangle by a centric stretch at the point . In the figure below, the blue triangle is translated into the (congruent) green triangle. Dilatations are one of the similarity maps . ${\displaystyle Z}$

Note: Axial affinities are not dilations.

Definitions

The definition of linear algebra for Desargue affine planes is equivalent to the definition of synthetic geometry, for non-Desargue planes only the synthetic definition makes sense and is therefore a generalization. There are also purely geometric definitions for higher-dimensional affine geometries, but these are then equivalent to the definition of linear algebra.

Linear Algebra

Let be a body or oblique body , a vector space or left vector space over , whose dimension over is at least 2, an affine space over , whose connection vectors form. Then an affinity is called dilatation if a scalar exists such that for two points it always holds. The scalar clearly determined by the dilation is called the stretch factor of . For is a translation. ${\displaystyle K}$ ${\displaystyle V}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle K}$ ${\displaystyle V\,}$ ${\displaystyle \alpha \colon {\mathcal {A}}\rightarrow {\mathcal {A}}}$ ${\displaystyle a\in K\setminus \{0\}}$ ${\displaystyle P,Q\in {\mathcal {A}}\,}$ ${\displaystyle {\overrightarrow {\alpha (P)\alpha (Q)}}=a\cdot {\overrightarrow {PQ}}\,}$ ${\displaystyle a}$ ${\displaystyle \alpha }$ ${\displaystyle a=1}$ ${\displaystyle \alpha }$

Synthetic geometry

Be an affine plane . A collineation, i.e. a straight bijection, is called dilation if one of the following equivalent conditions is met: ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \alpha \colon {\mathcal {A}}\rightarrow {\mathcal {A}}}$

1. Every straight line in the plane is parallel to its straight line in the image . ${\displaystyle g}$ ${\displaystyle \alpha (g)}$
2. The continuation of in the projective conclusion of is a projective perspective , in which the distance line is a fixed point line . ${\displaystyle \alpha }$ ${\displaystyle {\mathcal {A}}}$

Dilation groups

To an at least two-dimensional affine geometry means

• the group of dilations on dilatation group of , ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \Delta ({\mathcal {A}})}$ ${\displaystyle {\mathcal {A}}}$
• the group of dilatations with a fixed fixed point (generalized) extension group with a center , ${\displaystyle Z\in {\mathcal {A}}}$ ${\displaystyle \Delta _{Z}({\mathcal {A}})}$ ${\displaystyle Z}$
• the group of dilations without a fixed point together with the identity translation group . ${\displaystyle {\mathcal {T}}({\mathcal {A}})}$

properties

General

• Every dilation is an affinity.
• An affinity or collineation on an at least two-dimensional affine geometry is a dilation if and only if every straight line is parallel to its image straight line.
• If a dilatation has more than one fixed point, then it is the identical mapping .
• A dilation is clearly defined by specifying the image points for two different points in space.
• In the case of a non-identical dilation with a fixed point , the straight lines are exactly through fixed lines. ${\displaystyle Z}$ ${\displaystyle Z}$
• In the case of a non-identical translation , exactly the parallels to the connecting straight lines are fixed straight lines, with any point being. ${\displaystyle \tau \in {\mathcal {T}}({\mathcal {A}})}$ ${\displaystyle P\,\tau (P)}$ ${\displaystyle P\in {\mathcal {A}}}$
• In an affine geometry that satisfies the affine Fano axiom , every point reflection is a dilation.

Structure of the dilation groups

• The translation group is a normal part of the dilation group . ${\displaystyle \left({\mathcal {T}}({\mathcal {A}})\triangleleft \Delta ({\mathcal {A}})\right)}$
• To two points if a translation exists, on maps , then the generalized stretching groups in the Dilatationsgruppe conjugate subgroups - then applies - and isomorphic to each other. ${\displaystyle X,Y\in {\mathcal {A}}}$ ${\displaystyle \tau \in {\mathcal {T}}({\mathcal {A}})}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \left(\tau (X)=Y\right)}$ ${\displaystyle \Delta _{X}({\mathcal {A}}),\Delta _{Y}({\mathcal {A}})<\Delta ({\mathcal {A}})}$ ${\displaystyle \tau \Delta _{X}({\mathcal {A}})\tau ^{-1}=\Delta _{Y}({\mathcal {A}})}$

Desargue spaces

• In a -dimensional affine space ( ) over a sloping body we have: ${\displaystyle n}$ ${\displaystyle n\geq 2}$ ${\displaystyle K}$

1. A dilation is a translation if and only if the extension factor assigned to it is, otherwise it has a fixed point and it applies . ${\displaystyle \alpha }$ ${\displaystyle a=1}$ ${\displaystyle Z}$ ${\displaystyle \alpha \in \Delta _{Z}({\mathcal {A}})}$
2. The translation group is a commutative normal divisor of the dilatation group and, as a group, is isomorphic to the left vector space of the connecting vectors . ${\displaystyle K}$ ${\displaystyle \left(({\mathcal {T}}({\mathcal {A}}),\circ )\cong (K^{n},+)\right)}$
3. The extension groups to any centers are isomorphic to each other and to the multiplicative group of the oblique body . With the isomorphism to the multiplicative group of the oblique body, each stretching is assigned its stretching factor. ${\displaystyle \left((\Delta _{X}({\mathcal {A}}),\circ )\cong (\Delta _{Y}({\mathcal {A}}),\circ )\cong (K^{\ast },\cdot )\right)}$
4. The Dilatationsgruppe is the inner semi direct product of translation group with any stretching group: . ${\displaystyle \Delta ({\mathcal {A}})\cong {\mathcal {T}}({\mathcal {A}})\cdot \Delta _{Z}({\mathcal {A}})}$
5. In particular, each dilation can be clearly represented as a concatenation of a stretching around the firmly selected origin with a subsequent translation. ${\displaystyle \alpha }$ ${\displaystyle O\in {\mathcal {A}}}$
6. The Dilatationsgruppe is isomorphic to an outer semi direct product : . The operation from on is given by the left multiplication with the stretching factors. ${\displaystyle (\Delta ({\mathcal {A}}),\circ )\cong (K^{n},+)\times _{\theta }(K^{\ast },\cdot )}$ ${\displaystyle \theta }$ ${\displaystyle K^{\ast }}$ ${\displaystyle K^{n}}$
7. If there is a finite field with elements, then the dilation group contains elements. ${\displaystyle K}$ ${\displaystyle q}$ ${\displaystyle q^{n}\cdot (q-1)}$

Affine translation planes

• In an affine translation plane whose coordinate range is the left quasi-body and whose oblique body is the true-track endomorphisms of the translation group , the following applies: ${\displaystyle K}$ ${\displaystyle S=\operatorname {Kern} (K)}$

1. There is a constant for every dilation , so that it always holds for any point . As in Desargue's case, this constant is called the stretching factor of the dilation. A dilation is a translation if and only if its stretching factor is, otherwise it has a fixed point and it applies . ${\displaystyle \alpha }$ ${\displaystyle a\in S^{\ast }}$ ${\displaystyle P,Q\in {\mathcal {A}}}$ ${\displaystyle {\overrightarrow {\alpha (P)\alpha (Q)}}=a\cdot {\overrightarrow {PQ}}}$ ${\displaystyle \alpha }$ ${\displaystyle a=1}$ ${\displaystyle Z}$ ${\displaystyle \alpha \in \Delta _{Z}({\mathcal {A}})}$
2. The translation group is a commutative normal divisor of the dilation group and, as a group, is isomorphic to the left vector space of the displacements . ${\displaystyle S}$ ${\displaystyle \left(({\mathcal {T}},\circ )\cong (K^{2},+)\right)}$
3. The extension groups to any centers are isomorphic to each other and to the multiplicative group . In the isomorphism for the multiplicative group, each stretch is assigned its stretch factor. ${\displaystyle S=\operatorname {Kern} (K)}$ ${\displaystyle \left((\Delta _{X}({\mathcal {A}}),\circ )\cong (\Delta _{Y}({\mathcal {A}}),\circ )\cong (S^{\ast },\cdot )\right)}$ ${\displaystyle S^{\ast }}$
4. The Dilatationsgruppe is the inner semi direct product of translation group with any stretching group: . ${\displaystyle \Delta ({\mathcal {A}})\cong {\mathcal {T}}({\mathcal {A}})\cdot \Delta _{Z}({\mathcal {A}})}$
5. In particular, each dilation can be clearly represented as a concatenation of a stretching around the firmly selected origin with a subsequent translation. ${\displaystyle \alpha }$ ${\displaystyle O\in {\mathcal {A}}}$
6. The Dilatationsgruppe is isomorphic to an outer semi direct product: . The operation from on is given by the left multiplication with the stretching factors. ${\displaystyle (\Delta ({\mathcal {A}}),\circ )\cong (K^{2},+)\times _{\theta }(S^{\ast },\cdot )}$ ${\displaystyle \theta }$ ${\displaystyle S^{\ast }}$ ${\displaystyle K^{2}}$
7. If the quasi-body is finite and therefore a -dimensional vector space over its kernel, a finite body with elements, then the dilation group contains elements. ${\displaystyle K}$ ${\displaystyle r}$ ${\displaystyle q}$ ${\displaystyle q^{2r}\cdot (q-1)}$

Lengths, angles, volumes

Levels

• If there is an orthogonality relation between the straight lines in an affine incidence plane, then the orthogonality remains in the case of a dilation : If the plane is straight, then the following applies . This remains correct even if the orthogonality allows isotropic straight lines ( ). ${\displaystyle {\mathcal {A}}}$ ${\displaystyle \alpha }$ ${\displaystyle g,h}$ ${\displaystyle g\perp h\;\Leftrightarrow \;\alpha (g)\perp \alpha (h)}$ ${\displaystyle g\perp g}$
• In a pre-Euclidean plane :

1. The image of a right-angled coordinate system is again a right-angled coordinate system . The orthogonality constants with respect to and are equal. ${\displaystyle S=(O,E_{1},E_{2})}$ ${\displaystyle \alpha (S)=(\alpha (O),\alpha (E_{1}),\alpha (E_{2}))}$ ${\displaystyle S}$ ${\displaystyle \alpha (S)}$
2. If there is a pre-Euclidean plane with squares and a Cartesian coordinate system, then Cartesian is also . ${\displaystyle {\mathcal {A}}}$ ${\displaystyle S}$ ${\displaystyle \alpha (S)}$
3. Every dilation is true to a circle: the image of a circle is a circle.
4. The picture of a length class is a length class: If the arrows and are of the same length, then this also applies to their picture arrows and under a dilation . ${\displaystyle (P_{1},Q_{1})}$ ${\displaystyle (P_{2},Q_{2})}$ ${\displaystyle (\alpha (P_{1}),\alpha (Q_{1}))}$ ${\displaystyle (\alpha (P_{2}),\alpha (Q_{2}))}$ ${\displaystyle \alpha }$
5. If the stretching factor of a dilatation is 1 or −1, then this dilatation even maps each length class to itself. In other words: Exactly the translations and the point reflections are true-length dilatations.

• In a Euclidean plane or more generally in an arranged , freely movable plane with a length dimension for lines and an (oriented) angle dimension, the following applies:

1. The (oriented) angle measure is invariant under every dilation.
2. The following applies to the ratio of the length of a segment to the length of the image segment: Here are different points of the plane, the stretching factor of the dilation . In particular, the translations and point reflections are precisely length- true dilatations, and with each dilatation the ratios of any two line lengths are retained. ${\displaystyle |\alpha (P)\alpha (Q)|:|PQ|=|a|}$ ${\displaystyle P,Q\in {\mathcal {A}}}$ ${\displaystyle a}$ ${\displaystyle \alpha }$
3. If the plane is oriented, every dilation preserves orientation.

Note that the stretching factors can also be "infinite" numbers for planes over non- Archimedean ordered bodies . ${\displaystyle a}$

Spaces with a scalar product

In an at least two-dimensional affine space over a subfield of real numbers , in whose vector space the connection vector is declared a scalar product , the following applies: ${\displaystyle {\mathcal {A}}}$ ${\displaystyle K}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle K}$ ${\displaystyle V}$ ${\displaystyle \langle \cdot ,\cdot \rangle \colon V\times V\rightarrow \mathbb {R} }$

1. The scalar product of connection vectors always changes by the same factor for a dilation , more precisely: with the stretching factor of . ${\displaystyle \alpha }$ ${\displaystyle \langle {\overrightarrow {\alpha (P)\alpha (Q)}},{\overrightarrow {\alpha (R)\alpha (S)}}\rangle =a^{2}\cdot \langle {\overrightarrow {PQ}},{\overrightarrow {RS}}\rangle }$ ${\displaystyle a}$ ${\displaystyle \alpha }$
2. If a rigid subfield of the real numbers is a kind of inversion: If there is a mapping that satisfies the property for any point and every scalar product with the same constant , then there is a dilatation of with the stretching factor or . ${\displaystyle K}$ ${\displaystyle f\colon {\mathcal {A}}\rightarrow {\mathcal {A}}}$ ${\displaystyle \langle {\overrightarrow {f(P)f(Q)}},{\overrightarrow {f(R)f(S)}}\rangle =a^{2}\cdot \langle {\overrightarrow {PQ}},{\overrightarrow {RS}}\rangle }$ ${\displaystyle P,Q,R,S\in {\mathcal {A}}}$ ${\displaystyle V}$ ${\displaystyle a\in K^{\ast }}$ ${\displaystyle f}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle a}$ ${\displaystyle -a}$
3. The (non-oriented) angular measure defined with the help of the scalar product is invariant under every dilation.
4. The defined by means of the scalar product (square) of each connecting standard vector multiplied by the amount of stretch factor of a dilatation: . ${\displaystyle \|{\overrightarrow {\alpha (P)\alpha (Q)}}\|_{2}=|a|\cdot \|{\overrightarrow {PQ}}\|_{2}}$
5. In particular, the translations and point reflections are exactly length- true dilatations and with each dilatation the ratios of any two line lengths are retained.
   

   For angular orientation: form a triangle, is the center of the rotation around the angle at which the beam is rotated through the angular field to be measured . ${\displaystyle A,B,C\in {\mathcal {A}}}$ ${\displaystyle B}$ ${\displaystyle w(\angle ABC)}$ ${\displaystyle BA^{+}}$ ${\displaystyle BC^{+}}$
6. If there is a translation-invariant, -additive volume measure that is compatible with the norm , then this applies to measurable subsets . ${\displaystyle \sigma }$ ${\displaystyle \operatorname {vol} }$ ${\displaystyle M\subset {\mathcal {A}}:\,|\operatorname {vol} (\alpha (M))|=|a|^{n}\cdot |\operatorname {vol} (M)|}$
7. The image of a right-angled coordinate system under a dilatation is again a right-angled coordinate system.
8. In an oriented affine space of dimension over an arranged subfield of real numbers, the following applies: ${\displaystyle n\geq 2}$

• A dilatation is orientationally true if its stretching factor is positive or the dimension of the space is an even number, otherwise it reverses the orientation. ${\displaystyle n}$
• The amount of the oriented angular dimension of a directed angle is retained with each dilation. Compare the figures on the right and in the introduction! If the sign of the angle is taken into account, the following applies more precisely where is the sign function . ${\displaystyle w(\angle ABC)}$ ${\displaystyle \angle ABC}$ ${\displaystyle w(\angle \alpha (A)\alpha (B)\alpha (C))=\operatorname {sgn}(a)^{n}\cdot w(\angle ABC),}$ ${\displaystyle \operatorname {sgn} }$
• If there is an oriented, translation-invariant, additive volume measure compatible with the norm , then this applies to measurable, oriented subsets . ${\displaystyle \sigma }$ ${\displaystyle \operatorname {vol} }$ ${\displaystyle M\subset {\mathcal {A}}:\,\operatorname {vol} (\alpha (M))=a^{n}\cdot \operatorname {vol} (M)}$

Image construction, uniqueness and existence

In the main case , four different, coplanar points are specified or can be constructed from the specifications that form a non-degenerate trapezoid but not a parallelogram. The trapezoid can also be "overturned". The non-parallel sides of the trapezoid intersect at the center of the dilation. ${\displaystyle A_{1},A_{2},B_{1},B_{2}}$ ${\displaystyle Z}$

The following is always an at least two-dimensional affine geometry. The illustrations for the constructions in this section can also be understood spatially : The (up to four) default points always lie in a common plane of the geometry, in which the center is also, if it exists. There is no dilatation for specifications that are not on the same level. If the image point is to be constructed for a further point , then again all points involved in the construction lie in one plane, which however does not have to be that determined by the default points. All in all, all of the “constructions” described here take place in an at most three-dimensional affine subspace of the geometry . ${\displaystyle {\mathcal {A}}}$ ${\displaystyle C_{1}}$ ${\displaystyle {\mathcal {A}}}$

A fixed point is given

If there is a point-image point pair and a fixed point , then there is only a dilation with if ${\displaystyle A_{1},A_{2}}$ ${\displaystyle Z}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha (A_{1})=A_{2};\alpha (Z)=Z}$

1. the points are collinear and different, or ${\displaystyle Z,A_{1},A_{2}}$
2. ${\displaystyle A_{1}=A_{2}\neq Z}$is or
3. ${\displaystyle A_{1}=A_{2}=Z}$ is.

In the second case there is exactly one dilation with the required property: the identity of the space. In the third case, there is at least the identity that has the required property, in general there are further central dilatations with the required property, in the first case there is at most one dilatation with the required property. If a Desargue geometry, then such a dilatation exists, if an affine translation plane, then it exists if and only if are commensurable . The construction can be carried out as described below in the “main case”. Compare also the illustration on the right. ${\displaystyle {\mathcal {A}}}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle Z,A_{1},A_{2}}$

Two point-image point pairs given

If there are four different points of the geometry, then there is only a dilation with in the following cases ${\displaystyle A_{1},A_{2},B_{1},B_{2}}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha (A_{1})=A_{2};\alpha (B_{1})=B_{2}:}$

1. The four points form a parallelogram or ${\displaystyle A_{1}B_{1}B_{2}A_{2}}$
2. they form a - possibly also overturned - not degenerate trapezoid with , but (main case) or ${\displaystyle A_{1}B_{1}B_{2}A_{2}}$ ${\displaystyle A_{1}B_{1}\parallel A_{2}B_{2}}$ ${\displaystyle A_{1}A_{2}\not \parallel B_{1}B_{2}}$
3. they are collinear.

Collinear specifications

In the case of collinear specifications, you first construct 2 auxiliary points that do not lie on the same straight line as the specification points . ${\displaystyle H_{1},H_{2}}$ ${\displaystyle A_{1},A_{2},B_{1},B_{2}}$

The third case can be traced back to one of the other cases by the following construction:

• Pick any point outside of . ${\displaystyle H_{1}}$ ${\displaystyle A_{1}A_{2}}$
• Draw the straight lines connecting the triangle . ${\displaystyle A_{1}H_{1}B_{1}}$
• The parallel to through cuts the parallel to through at one point . ${\displaystyle A_{1}H_{1}}$ ${\displaystyle A_{2}}$ ${\displaystyle B_{1}H_{1}}$ ${\displaystyle B_{2}}$ ${\displaystyle H_{2}}$

So you now have a trapezoid and thus either the 1st or the 2nd case of the above case distinction (with in the place of ). A dilation fulfills the original specifications regardless of the choice of the auxiliary point exactly when it is fulfilled. ${\displaystyle A_{1}H_{1}H_{2}A_{2}}$ ${\displaystyle H_{1},H_{2}}$ ${\displaystyle B_{1},B_{2}}$ ${\displaystyle \alpha }$ ${\displaystyle H_{1}}$ ${\displaystyle \alpha (A_{1})=A_{2};\alpha (H_{1})=H_{2}}$

The specifications form a non-degenerate parallelogram

If the default points form a nondegenerate parallelogram, then the dilation (if it exists) must be a translation. One of the point-image point pairs is sufficient for the construction of further images, in the construction shown here was used. ${\displaystyle B_{1},B_{2}}$

In the first case, the dilation must be a non-identical translation, i.e. free of fixed points, compare the figure on the right. The image point can be constructed for any point (otherwise use ): The parallel to through intersects the parallel to through in ${\displaystyle C_{1}\not \in B_{1}B_{2}}$ ${\displaystyle A_{1},A_{2}}$ ${\displaystyle B_{1}B_{2}}$ ${\displaystyle C_{1}}$ ${\displaystyle B_{1}C_{1}}$ ${\displaystyle B_{2}}$ ${\displaystyle C_{2}.}$

The construction text shows that the dilatation, if it exists, is clearly determined by the specifications. It always exists for the 1st case if ${\displaystyle {\mathcal {A}}}$

• an affine translation plane, desarguess plane or
• is an at least three-dimensional affine geometry.

There are also affine levels that allow any in any direction parallel shifts: the affine excerpts of projective planes of Lenz class I .

The specifications form a trapezoid that is not a parallelogram

In the second case, the dilation is central if it exists . Compare the illustration for the “main case” earlier in this section.

• The center of the dilation is the intersection of the straight line with . ${\displaystyle Z}$ ${\displaystyle A_{1}A_{2}}$ ${\displaystyle B_{1}B_{2}}$

For any point (otherwise use ) the image point is constructed as follows: ${\displaystyle C_{1}\not \in B_{1}B_{2}}$ ${\displaystyle A_{1},A_{2}}$

• The parallel to through intersects the fixed line in ${\displaystyle B_{1}C_{1}}$ ${\displaystyle B_{2}}$ ${\displaystyle ZC_{1}}$ ${\displaystyle C_{2}.}$

It follows from the construction text that at most one dilation can meet the requirements. For specifications that correspond to the main case, there is always a dilatation, if ${\displaystyle {\mathcal {A}}}$

• is a desargue level,
• is an at least three-dimensional affine geometry or
• is an affine translation plane and the trapezoid with the center determined by it fulfills the requirements of the 1st ray theorem for translation planes. ${\displaystyle Z}$

literature

Dilation as defined in this article

• Wendelin Degen and Lothar Profke: Fundamentals of affine and Euclidean geometry . In: Mathematics for teaching at high schools . 1st edition. Teubner, Stuttgart 1976, ISBN 3-519-02751-8 ( table of contents [accessed on January 14, 2012]).
• Helmut Karzel, Kay Sörensen, Dirk Windelberg: Introduction to Geometry . In: Studia mathematica; University paperbacks . Paperback 1. Vandenhoeck and Ruprecht, Göttingen 1973, ISBN 3-525-03406-7 ( table of contents [accessed on January 14, 2012]).
• Max Koecher, Aloys Krieg: level geometry . 3., rework. and exp. Edition. Springer, Berlin / Heidelberg / New York 2007, ISBN 978-3-540-49327-3 ( table of contents [accessed January 14, 2012]).

Dilatation with a different meaning

• David Hilbert and Stephan Cohn-Vossen: Descriptive Geometry . 2nd Edition. Springer, Berlin / Heidelberg / New York 2011, ISBN 978-3-642-19947-9 ( table of contents [accessed on January 14, 2012]).
• Günter Scheja, Uwe Storch: Textbook of Algebra: including linear algebra . 2., revised. and exp. Edition. Teubner, Stuttgart 1994, ISBN 3-519-12203-0 ( table of contents [accessed on January 14, 2012]).

Web links

• Eric W. Weisstein : Dilation . In: MathWorld (English).

References and comments

1. ↑ Stefan E. Schmidt: Fundamentals of a general affine geometry . Springer-Verlag, 2013, ISBN 3-0348-9233-0 , p. 20.
2. ↑ Gerd Fischer: Analytical Geometry . Springer-Verlag, 2013, ISBN 3-322-96417-5 , p. 31.
3. ↑ Max Koecher, Aloys Krieg: level geometry . Springer-Verlag, 2007, ISBN 3-540-49328-X , p. 18
4. ^ Wilhelm Klingenberg: Linear Algebra and Geometry . Springer-Verlag, 2013, ISBN 3-642-77646-9 , p. 208
5. ^ P. Dembowski: Finite Geometries . Springer-Verlag, 1968, ISBN 3-642-62012-4 , p. 30.
6. ↑ ^{a b c} sword (1976)
7. ^ Koecher and War §2
8. ↑ A body is said to be rigid if it does not allow any body automorphisms apart from identity. Rigid body parts are z. B. itself, and the Archimedean ordered Euclidean solids. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$
9. ↑ ^{a b} “ Compatible with the norm” is an (oriented) volume measure if the (oriented) volume of the unit cuboid is 1.
10. ↑ Compare the 5th axiom for affine geometries .