Archimedes' axiom

Illustration of the Archimedean axiom: No matter how small the segment A is, if you only lay these segments together sufficiently often, the total length will be greater than for segment B.

The so-called Archimedean axiom is named after the ancient mathematician Archimedes , but it is older and was formulated by Eudoxus of Knidos in his theory of sizes. In modern terms it reads as follows:

For every two quantities there is a natural number with . ${\displaystyle y>x>0}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle nx>y}$

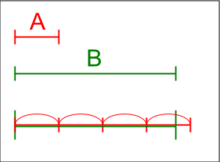
Geometrically, the axiom can be interpreted as follows: If you have two segments on a straight line, you can surpass the larger of the two if you only remove the smaller one often enough.

An ordered group or an ordered body , in which the Archimedean axiom applies, is called Archimedean (an) ordered .

For the field of real numbers it is sometimes introduced axiomatically . However, one can prove with the axioms of an ordered body and the supremum axiom ( every upwardly restricted subset of the body has a supremum ) that the real numbers are ordered Archimedes. ${\displaystyle \mathbb {R} }$

Proof from the supremum axiom for an ordered body

Be it ${\displaystyle x>0.}$

Assertion: For each there is a natural number such that it holds. ${\displaystyle y>x}$ ${\displaystyle n}$ ${\displaystyle nx>y}$

Counter-assumption: There is a such that for all natural numbers ${\displaystyle y>x}$ ${\displaystyle nx\leq y}$ ${\displaystyle n.}$

From the opposite assumption it follows that for all natural numbers there is an upper bound for . With the supremum axiom it follows from this the existence of a smallest upper bound . But if it applies to all natural numbers , then it also applies, and thus also to all natural numbers . But then there is also an upper bound for . Because of , is not a smallest upper bound, which contradicts the definition of . Thus the counter-assumption must be wrong and the claim is proven. ${\displaystyle y}$ ${\displaystyle n}$ ${\displaystyle nx}$ ${\displaystyle y_{0}}$ ${\displaystyle nx\leq y_{0}}$ ${\displaystyle n}$ ${\displaystyle \left(n+1\right)x\leq y_{0}}$ ${\displaystyle nx\leq y_{0}-x}$ ${\displaystyle n}$ ${\displaystyle y_{0}-x}$ ${\displaystyle nx}$ ${\displaystyle y_{0}-x<y_{0}}$ ${\displaystyle y_{0}}$ ${\displaystyle y_{0}}$

Consequences from the Archimedean axiom

For every number there is such that and . It follows that for every there exists a unique number with ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle n_{1},n_{2}\in \mathbb {N} }$ ${\displaystyle n_{1}>x}$ ${\displaystyle -n_{2}<x}$ ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle n\in \mathbb {Z} }$

${\displaystyle n\leq x<n+1.}$

It is denoted by or . There is also a clearly defined number with ${\displaystyle n}$ ${\displaystyle \lfloor x\rfloor }$ ${\displaystyle \operatorname {floor} (x)}$ ${\displaystyle m\in \mathbb {Z} }$

${\displaystyle m-1<x\leq m}$

which is denoted by or . This also applies: for everyone there is a with and therefore vice versa . This relationship is useful in analysis, for example to demonstrate the convergence or divergence of sequences . ${\displaystyle \lceil x\rceil }$ ${\displaystyle \operatorname {ceil} (x)}$ ${\displaystyle \varepsilon >0}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle n>1/\varepsilon }$ ${\displaystyle 1/n<\varepsilon }$

Furthermore, it follows from the Archimedean axiom that for two real numbers always a rational number with are, and that the set of natural numbers in the body is not limited to above. ${\displaystyle a,b\in \mathbb {R} ,a<b}$ ${\displaystyle q\in \mathbb {Q} }$ ${\displaystyle a<q<b}$ ${\displaystyle \mathbb {R} }$

Archimedean ordered groups

An ordered group is a group with a (here written additively) link and an order structure compatible with the group structure . ${\displaystyle +}$ ${\displaystyle \leq }$

The two axioms apply to the order structure:

Für alle  ${\displaystyle x\in G}$ gilt  ${\displaystyle x\leq x}$, das heißt  ${\displaystyle \leq }$ ist reflexiv.
Aus  ${\displaystyle x\leq y}$ und  ${\displaystyle y\leq z}$ folgt  ${\displaystyle x\leq z}$ für alle  ${\displaystyle x,y,z\in G}$, das heißt  ${\displaystyle \leq }$ ist transitiv.

In addition there is the axiom of group compatibility :

Aus  ${\displaystyle x\leq y}$ folgt  ${\displaystyle x+z\leq y+z}$ für alle  ${\displaystyle x,y,z\in G}$.

An ordered group is ordered according to Archimedes if:

Zu je zwei Elementen  ${\displaystyle x}$ und  ${\displaystyle y}$ der Gruppe mit  ${\displaystyle y>x>0}$ existiert eine natürliche Zahl  ${\displaystyle n\in \mathbb {N} }$ mit  ${\displaystyle nx>y}$.

Holder's theorem

Every Archimedean ordered group is commutative and isomorphic to an additively ordered subgroup of . ${\displaystyle G}$ ${\displaystyle \mathbb {R} }$

The figure is for a group linkage written with e> 0 and additively ${\displaystyle e\in G}$

${\displaystyle x\mapsto r=\sup \,\left\{{\frac {z}{n}}\mid z\in \mathbb {Z} ,n\in \mathbb {N} ,z\cdot e<n\cdot x\right\}}$

an isomorphism of G into an additive ordered subgroup of , where for and and for and . ${\displaystyle \mathbb {R} }$ ${\displaystyle n\cdot x=\underbrace {x+x+\dotsb +x} _{n{\text{-mal}}}}$ ${\displaystyle x\in G}$ ${\displaystyle n\in N}$ ${\displaystyle z\cdot e=-z\cdot (-e)}$ ${\displaystyle z\in Z}$ ${\displaystyle z<0}$

The element e can be used as a unit with which each group element can be "measured". This means: For each element of the group there is one such that . ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle r}$ ${\displaystyle x=r\cdot e(r\in \mathbb {R} )}$

Example : The intervals in music theory form an Archimedean ordered commutative group and can all be measured with the unit octave or cent . See: tone structure .

Classification : Either an Archimedean ordered group G is of the form G = {0} or G = {…, −3a, −2a, −a, 0, a, 2a, 3a, ...} (isomorphic to the additive group of the whole Numbers) or there is no smallest element, which is specified in the following.

There is a with for each element . (If there is no minimal positive , then there is certainly a with for each . If you can choose. If there is a with and if holds for the inequality .) ${\displaystyle a>0}$ ${\displaystyle b}$ ${\displaystyle 0<2b<a}$ ${\displaystyle a}$ ${\displaystyle a>0}$ ${\displaystyle c}$ ${\displaystyle 0<c<a}$ ${\displaystyle 2c<a}$ ${\displaystyle b=c}$ ${\displaystyle 2c=a}$ ${\displaystyle b}$ ${\displaystyle 0<2b<2c=a}$ ${\displaystyle 2c>a}$ ${\displaystyle b=a-c}$ ${\displaystyle 0<2b=2a-2c<2a-a=a}$

Non-Archimedean arranged bodies

An example of an arranged field in which the axiom of Archimedes does not apply is the field of hyperreal numbers studied in nonstandard analysis .

A simpler example consists of the rational functions over the rational (or real) number field, which are ordered so that is greater than all numbers (this can be done in a unique way). ${\displaystyle R(x)}$ ${\displaystyle x}$

Historical

In the elements in Book 3 Proposition 16, Euclid gives an explicit example of quantities that do not fulfill Archimedes' axiom, so - called horn - shaped angles that are formed by touching curved curves, in Euclid's example by a circle and its tangent. They only appear at this point in the elements.

Web links

Wikibooks: Math for Non-Freaks: Archimedes' Axiom  - Learning and Teaching Materials

Individual evidence

1. ↑ Narrated in: Euclid, elements V, definition 4: That they have a relationship to one another is said of quantities which, when multiplied, exceed one another.
2. ↑ Otto Hölder The axioms of quantity and the doctrine of measure , Ber. Verh. Saxon Society of Sciences Leipzig, Math. Phys. Class, Volume 53, 1901, pp. 1-64.
3. ↑ Alexander Gennadjewitsch Kurosch lectures on general algebra. Harri Deutsch, Zurich 1964.
4. ^ Euclid, Book 3, Proposition 16, in David Joyce
5. ^ Felix Klein Elementary Mathematics from the Higher Viewpoint , Springer Verlag, Volume 2, pp. 221f.