Sylvester-Gallai's theorem

The Sylvester-Gallai theorem is a mathematical theorem of plane geometry . It says that for every finite set of points that are not all on a straight line but in a plane , there is a straight line that contains exactly two points of the set. It is named after James Joseph Sylvester , who first formulated the statement in the Educational Times in 1893 , and Tibor Gallai , who published the first evidence in 1944 after Paul Erdős re-posed the problem in 1943. The first known evidence comes from Eberhard Melchior in 1940.

statement

Let be a finite set of points lying in a plane that do not all lie on a straight line. Then there is a straight line that contains exactly two points of . ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {P}}}$

An alternative equivalent formulation reads:

Let be a finite set of points on the plane with the following property: On every straight line through two points there is at least a third point of this set. Then all points lie on a straight line. ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {P}}}$

The statement also applies in unchanged form in higher-dimensional spaces; by choosing three points that do not lie on a straight line and considering the plane determined by them, the problem can be reduced to the two-dimensional case.

proof

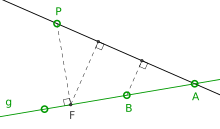
The following evidence goes back to Leroy Milton Kelly . It is often cited as a prime example of elegant evidence.

We consider pairs consisting of a straight line through two points and a point that does not lie on. Since not all points are on a straight line, there are such pairs, since the set is finite, there are also only finitely many such pairs. So that we can a pair of select, so that the distance , the by , has minimal is. It remains to show that it possesses the desired property, i.e. that there is no third point that lies on it. ${\displaystyle (g,P)}$ ${\displaystyle g}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle P\in {\mathcal {P}}}$ ${\displaystyle g}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle (g,P)}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle g}$ ${\displaystyle {\mathcal {P}}}$

Constellation of the points and lines in the decisive proof step

Let us assume that there are three such points. First be the base of the perpendicular from on . According to the drawer principle, there are then two points of which lie on the same side of on , these are and , where is closer to than . Then the distance from to the straight line through and smaller than the distance from zu , because it is at most as large as the distance from zu , which as the height in the right triangle is smaller than the length of the cathetus . ${\displaystyle F}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle F}$ ${\displaystyle g}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle F}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle F}$ ${\displaystyle AP}$ ${\displaystyle APF}$ ${\displaystyle PF}$

This is a contradiction to the choice of , because the straight line goes through and thus together with the point forms a pair with a smaller distance. So the assumption must be wrong, there are exactly two points on display as desired . ${\displaystyle (g,P)}$ ${\displaystyle A}$ ${\displaystyle P}$ ${\displaystyle B}$ ${\displaystyle g}$ ${\displaystyle {\mathcal {P}}}$

There are a number of other proofs for the Sylvester-Gallai theorem. So could HSM Coxeter show that the order axioms alone enough already to prove the concept of a distance is therefore not necessary.

Further evidence comes from Robert Steinberg (see below), Robert Creighton Buck , Norman Steenrod , Abraham Robinson , GDW Lang (1955) and VC Williams (1968) , among others . A proof of the equivalent projective-dual theorem comes from Eberhard Melchior (* 1912) from 1940 and is therefore the first proof. He uses Euler's polyhedron substitute in projective form.

application

The Fano plane consists of 7 points and 7 lines, with three points on each line. Therefore one of the straight lines must be represented as a circle.

A direct consequence of the Sylvester-Gallai theorem is the fact that the Fano plane cannot be embedded in the Euclidean plane.

The theorem also applies in the projective plane ( Robert Steinberg ), so that one can derive the dual statement: For a finite set of straight lines that do not all pass through a point, there is a point that lies on exactly two of these straight lines.

Generalizations

According to Sylvester-Gallai's theorem, for every finite, non-collinear set of points, there is at least one straight line that goes through exactly two of the points. By Dirac and Motzkin presumption comes that there will be even points at least are of such lines. On the other hand, constructions are known for even numbers in which precisely such straight lines actually exist, so that the bound cannot be improved. If odd, there are arrangements of points for which there are straight lines that contain exactly two of the points. Ben Green and Terence Tao were able to show that these limits can not be improved, at least for large ones, so there is a constant , so that for each one applies: If points are not on a straight line, there are at least (for even ) or (for odd ) Straight lines that go through exactly two of the points. ${\displaystyle n}$ ${\displaystyle \lfloor n/2\rfloor }$ ${\displaystyle n}$ ${\displaystyle n/2}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 3\lfloor n/4\rfloor }$ ${\displaystyle n}$ ${\displaystyle n_{0}}$ ${\displaystyle n>n_{0}}$ ${\displaystyle n}$ ${\displaystyle n/2}$ ${\displaystyle n}$ ${\displaystyle 3\lfloor n/4\rfloor }$ ${\displaystyle n}$

literature

• Martin Aigner , Günter M. Ziegler : The book of evidence . Springer, Berlin, 4th edition, 2015. ISBN 978-3-662-44456-6 . Chapter 11: Straight lines in the plane and decompositions of graphs.
• Peter Borwein , William Oscar Jules Moser : A survey of Sylvester's problem and its generalizations , Aequationes Mathematicae, Volume 40, 1990, pp. 111-135, pdf

Individual evidence

1. ^ Sylvester, Mathematical Question 11851, Educational Times, Volume 59, 1893, p. 98.
2. ^ Gallai, Problem 4065, American Mathematical Monthly, Volume 51, 1944, pp. 169-171.
3. ↑ Erdős, Problem 4065, American Mathematical Monthly, Volume 50, 1943, p. 65.
4. ↑ Eberhard Melchior: About versatility of the projective level. In: Deutsche Mathematik, Volume 5, 1940, pp. 461-475. The address given in the work was Munich. His proof is presented in S. Felsner: Geometric Graphs and Arrangements. Vieweg, 2004, p. 72 f.
5. ↑ Published in HSM Coxeter , A problem of collinear points , American Mathematical Monthly, Volume 55, 1948, pp. 26-28.
6. ↑ ^{a b} Erdős, Solution to problem 4065, American Mathematical Monthly, Volume 51, 1944, pp. 169-171.
7. ↑ See Motzkin, The lines and planes connecting the points of a finite set, Trans. Amer. Math. Soc., Vol. 70, 1951, pp. 451-464.
8. ^ Lang, The dual of a well known problem, Mathematical Gazette, Volume 39, 1955, p. 314.
9. ^ Williams, A proof of Sylvester's theorem on collinear points, American Mathematical Monthly, Volume 75, 1968, pp. 980-982.
10. ↑ Melchior, About Versatile of Projective Plane, German Mathematics, Volume 5, 1940, pp. 461–475. Shown in S. Felsner Geometric Graphs and Arrangements , Vieweg 2004, p. 72f
11. ^ R. Steinberg, Three point collinearity, American Mathematical Monthly, Volume 51, 1944, pp. 169-171. A projective proof.
12. ^ GA Dirac: Collinearity Properties of Sets of Points. In: The Quarterly Journal of Mathematics. 1951, Vol. 2. pp. 221-227. doi: 10.1093 / qmath / 2.1.221 , Th. Motzkin: The lines and planes connecting the points of a finite set. In: Transactions of the American Mathematical Society. 1951, Vol. 70. pp. 451-464. doi: 10.2307 / 1990609
13. ^ DW Crowe, TA McKee: Sylvester's Problem on Collinear Points. In: Mathematics Magazine. 1968, vol. 41, no. 1. pp. 30-34. doi: 10.2307 / 2687957
14. ↑ Ben Green, Terence Tao: On Sets Defining Few Ordinary Lines. In: Discrete & Computational Geometry. 2013, Vol. 50, No. 2. pp. 409-468. doi: 10.1007 / s00454-013-9518-9