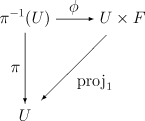Fiber bundle

In mathematics , especially in topology , a fiber bundle is a space that locally looks like a product : Fiber bundles can be understood as continuous surjective mappings with a local triviality condition: for each point of there is an environment for which the restriction projection of one Product with a fiber . ${\ displaystyle \ pi \ colon E \ to B}$ ${\ displaystyle B}$ ${\ displaystyle U}$ ${\ displaystyle \ pi | _ {\ pi ^ {- 1} (U)}}$ ${\ displaystyle U \ times F}$ ${\ displaystyle F}$

${\ displaystyle E, B}$ and are called total space , base and fiber of the bundle. There are various generalizing terms of the term fiber bundle of fibers , in particular Serre and Hurewicz fibers . ${\ displaystyle F}$

Special fiber bundles are z. B. vector bundles , which play a fundamental role in the mathematical formulation of physical gauge theory .

definition

A fiber bundle is specified by the data , where , and are topological spaces and the projection is a continuous surjective map which is locally trivializable, i.e. H. it exists for each point in an open environment , so that it is homeomorphic to space , provided with the product topology , and the following diagram commutes: ${\ displaystyle (E, B, \ pi, F)}$ ${\ displaystyle E}$ ${\ displaystyle B}$ ${\ displaystyle F}$ ${\ displaystyle \ pi \ colon E \ to B}$ ${\ displaystyle x}$ ${\ displaystyle B}$ ${\ displaystyle U}$ ${\ displaystyle \ pi ^ {- 1} (U)}$ ${\ displaystyle U \ times F}$

where is the natural projection on the first factor and a homeomorphism. The set of all such is called the local trivialization of the bundle and by definition they cover the base. ${\ displaystyle \ operatorname {proj} _ {1} \ colon U \ times F \ to U}$ ${\ displaystyle \ phi \ colon \ pi ^ {- 1} (U) \ to U \ times F}$ ${\ displaystyle \ {(U_ {i}, \ phi _ {i}) \}}$ ${\ displaystyle U_ {i}}$

For each out the archetype is homeomorphic to and is called fiber over . A fiber bundle is often represented by the short exact sequence . Note that each fiber bundle is an open image , since projections of products are open images. Therefore, the quotient topology induced by the mapping carries . ${\ displaystyle x}$ ${\ displaystyle B}$ ${\ displaystyle \ pi ^ {- 1} (x)}$ ${\ displaystyle F}$ ${\ displaystyle x}$ ${\ displaystyle (E, B, \ pi, F)}$ ${\ displaystyle F \ longrightarrow E \ {\ xrightarrow {\, \ \ pi \}} \ B}$ ${\ displaystyle \ pi \ colon E \ to B}$ ${\ displaystyle B}$ ${\ displaystyle \ pi}$

A fiber bundle is a special case of Serre fiber , that is, it has the so-called homotopy elevation property for images of CW complexes .

Examples

The Möbius strip is a nontrivial bundle over S ¹ with fibers [0,1].

The Klein bottle is a nontrivial bundle over S ¹ with fiber S ¹ .

Be and the projection on the first factor. Then a bundle of fibers is over with fiber . In this case, a product space is not only local, but even global . Such a fiber bundle is called a trivial bundle . ${\ displaystyle E = B \ times F}$ ${\ displaystyle \ pi \ colon E \ to B}$ ${\ displaystyle E}$ ${\ displaystyle B}$ ${\ displaystyle F}$ ${\ displaystyle E}$

A simple example of a nontrivial bundle is the Möbius strip . The base is here (the circular line ), the fiber a closed interval. The corresponding trivial bundle would be a cylinder , from which the Möbius strip differs by twisting the fiber. This rotation is only visible globally, the cylinder and Möbius strip are locally identical. ${\ displaystyle B}$ ${\ displaystyle S ^ {1}}$ ${\ displaystyle F}$

A similar nontrivial bundle is the Klein bottle , which has a fiber structure over it. The corresponding trivial bundle would be a torus . Each fiber bundle across is an imaging torus . ${\ displaystyle S ^ {1}}$ ${\ displaystyle S ^ {1}}$ ${\ displaystyle S ^ {1}}$

Each overlay of a contiguous space is a fiber bundle with a discrete fiber.

A special class of fiber bundles, the vector bundles , are characterized by the fact that their fibers are vector spaces and the trivializations are linear fiber by fiber . Important examples here are the tangential and cotangential bundles of a manifold .

Another special class of fiber bundles are the principal bundles or main fiber bundles .

Cuts

→ Main article: Cut (bundle of fibers)

Under a global average is defined as a continuous map such that for all of . The theory of characteristic classes in algebraic topology deals with the existence of global sections. ${\ displaystyle f \ colon B \ to E}$ ${\ displaystyle \ pi (f (x)) = x}$ ${\ displaystyle x}$ ${\ displaystyle B}$

Often you can only define sections locally. A local section is a continuous mapping , which is an open set in and for all out . This is always possible for local trivialization . These cuts are equivalent to continuous images that form a sheaf . ${\ displaystyle f \ colon U \ to E}$ ${\ displaystyle U}$ ${\ displaystyle B}$ ${\ displaystyle \ pi (f (x)) = x}$ ${\ displaystyle x}$ ${\ displaystyle U}$ ${\ displaystyle (U, \ phi)}$ ${\ displaystyle U \ to F}$

Structural groups

With the exception of topological equivalence, fiber bundles are characterized by “atlases” that indicate how their local trivializations are “stuck together”: Let be a topological group that acts on the fiber from the left by means of an effective effect . A - Atlas of the bundle consists of local trivializations, so that for any two overlapping maps and the endomorphism ${\ displaystyle G}$ ${\ displaystyle F}$ ${\ displaystyle G}$ ${\ displaystyle (E, B, \ pi, F)}$ ${\ displaystyle (U_ {i}, \ phi _ {i})}$ ${\ displaystyle (U_ {j}, \ phi _ {j})}$

{\ displaystyle \ phi _ {i} \ phi _ {j} ^ {- 1} \ colon (U_ {i} \ cap U_ {j}) \ times F \ to (U_ {i} \ cap U_ {j} ) \ times F}

by

{\ displaystyle \ phi _ {i} \ phi _ {j} ^ {- 1} (x, \ xi) = (x, t_ {ij} (x) \ xi)}

is given, where is a continuous mapping. Two atlases are equivalent if their union is also an atlas. A bundle is a bundle of fibers together with an equivalence class of atlases. The group is called the structural group of the bundle. Each fiber bundle can be described by an atlas if we choose the automorphism group of the fiber as the structural group; if we choose smaller, the fiber bundle gains additional structure. ${\ displaystyle t_ {ij} \ colon U_ {i} \ cap U_ {j} \ to G}$ ${\ displaystyle G}$ ${\ displaystyle G}$ ${\ displaystyle G}$ ${\ displaystyle G}$ ${\ displaystyle G}$ ${\ displaystyle G}$ ${\ displaystyle G}$

Because the map changes describe the transition between local trivializations, they satisfy the Cozykel condition (see also Čech cohomology ); in particular follow and . ${\ displaystyle t_ {ij}}$ ${\ displaystyle t_ {ik} (x) = t_ {ij} (x) t_ {jk} (x)}$ ${\ displaystyle t_ {ii} (x) = \ operatorname {id} _ {U_ {i}}}$ ${\ displaystyle t_ {ij} (x) = t_ {ji} (x) ^ {- 1}}$

A principal bundle is a bundle in which the fiber is identified and on which a fiber-preserving legal effect on total space is explained. ${\ displaystyle G}$ ${\ displaystyle G}$ ${\ displaystyle G}$

literature

Norman Steenrod : The Topology of Fiber Bundles. Princeton University Press, Princeton NJ 1951 ( Princeton Mathematical Series 14, ISSN 0079-5194 ), (7. printing, and 1. paperback printing. Ibid 1999, ISBN 0-691-00548-6 ( Princeton Landmarks in Mathematics and Physics. = Princeton Paperbacks )).
David Bleecker: Gauge Theory and Variational Principles. Addison-Wesley publishing, Reading MA 1981, ISBN 0-201-10096-7 , chapter 1.
Martin Schottenloher: Geometry and Symmetry in Physics. The leitmotif of mathematical physics. Vieweg, Braunschweig et al. 1995, ISBN 3-528-06565-6 ( Vieweg textbook Mathematical Physics ).