Vector bundle

Vector bundles or sometimes also vector space bundles are families of vector spaces that are parameterized by the points of a topological space . Vector bundles therefore also belong to the fiber bundles . If there is a set of bases for each vector space of the vector bundle , then this set can also form a fiber bundle. One then speaks of frame bundles or also re bundles. These special fiber bundles are also main fiber bundles .
A vector bundle clearly consists of one vector space for each point of the base space. However, since vector spaces of the same dimension are always isomorphic, the essential information lies in the relationships between these vector spaces. The best known example of a vector bundle is the tangential bundle of a differentiable manifold . The relationship between the various tangential spaces, i.e. the vector spaces for the individual points, is expressed, for example, in the question of whether a vector field is differentiable.
The question of how vector bundles can look in a space is closely related to global topological properties of space. Non-isomorphic vector bundles can often be distinguished by their characteristic classes .
Definitions
Vector bundle
Let be a real or a complex n-dimensional vector space. A real or complex vector bundle of rank is a triple , consisting of topological spaces ( total space ) and ( base ) as well as a continuous surjective mapping , so that:
- For each point of the fiber contributes from about the structure of a real or complex n -dimensional vector space .
- “Local triviality”: For each point there is an environment of and a homeomorphism
- ,
- who is compatible with , that is , and for the
- for each in one isomorphism is of vector spaces. The projection on the first factor denotes . Such is called local trivialization .
A vector bundle is called trivial if there is a trivialization with . is a trivial bundle of vectors.
In abbreviated form one often speaks of the "vector bundle ", which implicitly denotes the triple .
Line bundle
A vector bundle with rank 1 is called a straight line bundle (as a mistranslation from English also a line bundle ).
Examples
- The tangent bundle of a differentiable manifold is a vector bundle consisting of the tangent spaces of the manifold. Correspondingly, the cotangential bundle consisting of the cotangential spaces - that is, the dual spaces of the tangential spaces - is a vector bundle.
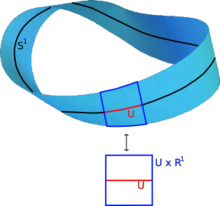
- The Möbius strip is a bundle of straight lines over the 1-sphere ( circle ) . Locally it is homeomorphic to , where is an open subset of . However, the Möbius strip is not homeomorphic to what a cylinder would be.
- As a bundle of external algebra , the space of differential forms is also a vector bundle.
- The - tensor bundle is also a vector bundle that includes the vector bundles listed above as special cases.
Homomorphism of vector bundles
Homomorphism
A vector bundle homomorphism from the vector bundle into the vector bundle is a pair of continuous maps and , such that
- applies and
- is a linear map for all .
A vector bundle homomorphism is often referred to as a bundle homomorphism or a homomorphism for short.
Isomorphism
A vector bundle homomorphism from to is a vector bundle isomorphism if and are homeomorphisms and the induced linear mapping is a vector space isomorphism .
example
Looking at the district as a manifold, then the tangent from isomorphic to the trivial vector bundle . The homeomorphism between the base spaces is the identical mapping and that between the total spaces reads
for and .
Substructures
Sub-vector bundle
The fibers of the vector bundle at the point are designated with. A sub-vector bundle of the vector bundle consists of a topological subspace consisting of a family of sub-vector spaces of , so that is a separate vector bundle.
Restricted vector bundle
The fibers of the vector bundle at the point are again designated with and designates a topological subspace. The restricted vector bundle is defined by
- .
The restricted vector bundle is an independent vector bundle with regard to the topological subspace .
Constructions with vector bundles
Withdrawn vector bundle
For a vector bundle and a continuous mapping , the withdrawn vector bundle ("pull-back" or "induced bundle", see also return transport ) is defined as the bundle over with total space
and projection . The vector space structure is defined by . One can show that this again defines a locally trivial vector bundle.
The following applies to the mapping defined by and for each induces a vector space isomorphism .
For each bundle mapping one has an isomorphism , where the mapping that belongs to is the bases.
Direct product, Whitney sum, tensor product
For two vector bundles the direct product is defined as
each fiber is provided with the vector space structure as the direct sum of the vector spaces and .
Now let's be vector bundles over the same base, so . Your Whitney sum is then defined as a withdrawn bundle using the diagonal mapping
- .
The Whitney sum is just the vector bundle over whose fiber is over the direct sum .
Similarly, the tensor product is defined as the vector bundle whose fiber is over the tensor product .
Other objects in vector bundles
cut
If an open subset of , then a mapping is called
for which applies a cut of over . The set of all cuts from over forms a vector space.
frame
A frame (English frame , French repère ) is a kind of base of a vector bundle. There are n linearly independent vectors for each fiber. These vectors form a base of the fiber at each point . This means precisely:
Let be a vector bundle with rank and be an open subset of the base space. A local reper or frame of over is an ordered n-tuple . There is a cut in over for all i , so that a base of the fiber forms for all . If one can choose, one speaks of a global framework.
Vector bundles with additional structures
Differentiable vector bundle
Be a vector bundle. If and are differentiable manifolds and if the projection as well as the trivializations are differentiable, then the vector bundle is called differentiable . It is said to be smooth if the manifolds are smooth and the mappings can be differentiated any number of times.
Holomorphic vector bundle
A holomorphic vector bundle is a complex vector bundle over a complex manifold , so that the total space is a complex manifold and the projection is a holomorphic mapping .
G vector bundle
Be a group. If and are G-spaces , then a vector bundle is a G-vector bundle if the group action
is a linear map for all .
Classifying space and classifying picture
The classifying space for -dimensional real vector bundles is the Graßmann manifold of -dimensional subspaces in , this is called. That means: every -dimensional real vector bundle is of the form for a continuous mapping (the so-called classifying mapping of the bundle) and the tautological bundle , and two bundles are isomorphic if and only if their classifying mappings are homotopic .
Analogously , the Graßmann manifold of the -dimensional subspaces in , the classifying space for -dimensional complex vector bundles.
Stable vector bundles
Two vector bundles and are called stable equivalent if there are trivial vector bundles (not necessarily of the same dimension) with
gives. The equivalence classes of this equivalence relation are called stable vector bundles . (This definition has no connection with the concept of stable vector bundles in algebraic geometry.)
Let it be and the ascending associations (i.e. the colimites with regard to the inclusions defined by means of and ), then one can consider a vector bundle and its classifying mapping or the composition with the inclusion or . Two vector bundles are stable equivalent if and only if the corresponding mappings or are homotopic.
Vector bundles in algebraic geometry
definition
For (algebraic) vector bundles in algebraic geometry are and schemes , is for all the points of a vector space, and the local trivialization are isomorphisms
In algebraic geometry, however, “vector bundle” usually means a locally free sheaf (see below).
Local-free sheaf
Let it be a locally small space, e.g. B. a topological space with the sheaf of continuous real or complex-valued functions, a differentiable manifold with the sheaf of -functions or a scheme .
A locally free sheaf is a - module , the locally isomorphic to a free is module d. H. can be covered by open sets for which is isomorphic to a direct sum of copies of .
Local-free sheaves and vector bundles
In the case of topological spaces or differentiable manifolds, the following two constructions provide an equivalence of the categories of locally free sheaves and vector bundles (for the sake of simplicity of the notation, the case of real vector bundles is described over a topological space):
- The sheaf of its cuts is assigned to a vector bundle.
- The disjoint union of its fibers is assigned to a locally free sheaf . We choose an open coverage of so that on each one becomes trivial. A trivialization nowhere defines disappearing cuts from over , which fiber by fiber form a base. These define a mapping
- ,
- and we define the topology by requiring that these mappings be homeomorphisms. It is well defined because these mappings differ over the intersection of two sets and only by one homeomorphism (more precisely, a continuously varying vector space automorphism of ).
In the case of algebraic geometry, this design is somewhat simpler: the bundle to a locally free sheaf is
here denotes the symmetrical algebra and the algebra spectrum .
Additional terms
- The investigation of so-called stable equivalence classes of vector bundles is the subject of K-theory .
- On algebraic curves have (semi) stable vector bundles particularly good properties.
literature
- R. Abraham, JE Marsden , T. Ratiu: Manifolds, Tensor Analysis, and Applications . 2nd Edition. Springer, Berlin 1988, ISBN 3-540-96790-7 (English).
- Allen Hatcher: Vector Bundles & K-Theory. Version 2.1, May 2009, (math.cornell.edu; PDF; 1.11 MB) .
- Karlheinz Knapp: vector bundle . Springer Fachmedien, Wiesbaden 2013, ISBN 978-3-658-03113-8 .
Web links
Individual evidence
- ^ Thomas Friedrich: Dirac operators in Riemannian geometry . 1st edition. Vieweg, 1997, ISBN 3-528-06926-0 .
- ↑ John Baez , Javier P. Muniain: Gauge fields, knots and gravity (= Series on knots and everything. 4). World Scientific, Singapore et al. 1994, ISBN 981-02-2034-0 , p. 200.
- ↑ Graeme Segal: Equivariant K-theory ( Memento from June 22, 2010 in the Internet Archive )