Laguerre plain

A Laguerre plane , named after Edmond Laguerre , is in the classical case an incidence structure that essentially describes the geometry of the curves given by an equation of form , that is, straight lines and parabolas, in the real plane of observation. Points with the same x-coordinates have no connection, so they are called parallel . ${\displaystyle y=ax^{2}+bx+c}$

Classic Laguerre plane: plane model

Laguerre plain: stereographic projection

Obviously, the following applies: 3 non-parallel points have exactly one connecting curve (straight line or parabola). Two such curves intersect at a maximum of 2 points and can touch in a common tangent . However, there are parabolas which intersect at only one point but do not touch: for example, intersect and only at the point (1,1) there and have no common tangent (see picture.). In order to exclude such cases from the contact relation, the far point is added to each curve . These curves are called cycles . The curves completed in this way now have the further intersection . The following statements apply to this extended system of points and cycles (see Möbius plane ): ${\displaystyle p_{1}:y=x^{2}}$ ${\displaystyle p_{2}:y=(x-2)^{2}}$ ${\displaystyle y=ax^{2}+bx+c}$ ${\displaystyle (\infty ,a)}$ ${\displaystyle p_{1},p_{2}}$ ${\displaystyle (\infty ,1)}$

• (B1): For every 3 pairs of non-parallel points, there is exactly one cycle that contains. ${\displaystyle A,B,C}$ ${\displaystyle z}$ ${\displaystyle A,B,C}$
• (B2): For each point and each of Cycles there is exactly one point on which to parallel (s image.). ${\displaystyle A}$ ${\displaystyle z}$ ${\displaystyle B}$ ${\displaystyle z}$ ${\displaystyle A}$
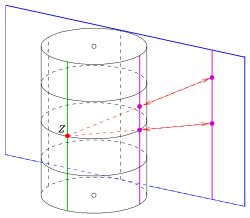
• (B3): (Berührrelation) For every Cycles , each point on and each point not on , to be not parallel , there is exactly one Cycles by which in contacts (s image.). ${\displaystyle z}$ ${\displaystyle P}$ ${\displaystyle z}$ ${\displaystyle Q}$ ${\displaystyle z}$ ${\displaystyle P}$ ${\displaystyle z^{\prime }}$ ${\displaystyle P,Q}$ ${\displaystyle z}$ ${\displaystyle P}$

As with the Möbius planes, it is not to be expected that the geometry of the extended straight lines and parabolas described here is the only incidence structure that has the properties (B1), (B2), (B3). If the real numbers are replaced here by any number field , (B1), (B2), (B3) remain valid (in contrast to the case of the Möbius plane).

In addition to the formally inhomogeneous model (there are straight lines and parabolas), a homogeneous spatial model is obtained with the help of the inversion of a suitable stereographic projection of the real plane onto a circular cylinder : The points of the new incidence structure are the points on the cylinder surface, the cycles are ellipses / Circles and parallel points lie on a straight cylinder. The classic real Laguerre plane can also be understood as the geometry of the plane sections (ellipses / circles) on a circular cylinder.

A Laguerre level is one of the 3 Benz levels : Möbius level, Laguerre level and Minkowski level . The classic Möbius plane is the geometry of the circles and the classic Minkowski plane is the geometry of the hyperbolas .

Comment:

1. A Laguerre plane was originally defined as the geometry of directed circles and straight lines in the real plane.
2. In addition to the previously mentioned geometric descriptions of the classic real Laguerre plane, there is also the representation above the ring of the dual numbers (analogous to the description of the classic Möbius plane above the complex numbers ).

The axioms of a Laguerre plane

Let it be an incidence structure with the set of points and the set of cycles . Two points are parallel ( ) if is or there is no cycle containing and . is called the Laguerre plane if the following axioms are fulfilled: ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {Z}}}$
${\displaystyle A,B}$ ${\displaystyle A\parallel B}$ ${\displaystyle A=B}$ ${\displaystyle A}$ ${\displaystyle B}$
${\displaystyle {\mathcal {L}}}$

Laguerre plane: axioms

(B1): For every 3 points , not parallel in pairs, there is exactly one cycle that contains. ${\displaystyle A,B,C}$ ${\displaystyle z}$ ${\displaystyle A,B,C}$

(B2): For every point and every cycle there is exactly one point with . ${\displaystyle P}$ ${\displaystyle z}$ ${\displaystyle P'\in z}$ ${\displaystyle P\parallel P'}$

(B3): (Axiom of contact) For every cycle , every point and every point that is not parallel to , there is exactly one cycle through with , ${\displaystyle z}$ ${\displaystyle P\in z}$ ${\displaystyle Q\notin z}$ ${\displaystyle P}$ ${\displaystyle z'}$ ${\displaystyle P,Q}$ ${\displaystyle z\cap z'=\{P\}}$

d. H. and touch at the point . ${\displaystyle z}$ ${\displaystyle z'}$ ${\displaystyle P}$

(B4): Every cycle contains at least 3 points, there is at least one cycle. There are at least 4 points not on a cycle.

Four points are concyclic if there is a cycle with . ${\displaystyle A,B,C,D}$ ${\displaystyle z}$ ${\displaystyle A,B,C,D\in z}$

From the definition of the property and axiom B2 follows ${\displaystyle \parallel }$

• The relation is an equivalence relation . ${\displaystyle \parallel }$

Motivated by the classic cylinder model, we are introducing the following designation:

a) For suppose b) An equivalence class is called generating . ${\displaystyle P\in {\mathcal {P}}}$ ${\displaystyle {\overline {P}}:=\{Q\in {\mathcal {P}}\ |\ P\parallel Q\}\quad .}$ ${\displaystyle {\overline {P}}}$

In the classic Laguerre plane, a generating line is a line parallel to the y-axis (plane model) or a straight line on the cylinder (cylinder model).

The connection to linear geometry is provided by the following term:

For a Laguerre plain we define the local structure ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$

${\displaystyle {\mathcal {A}}_{P}:=({\mathcal {P}}\setminus \{{\overline {P}}\},\{z\setminus \{{\overline {P}}\}\ |\ P\in z\in {\mathcal {Z}}\}\cup \{{\overline {Q}}\ |\ Q\in {\mathcal {P}}\setminus \{{\overline {P}}\},\in )}$

and name it the derivative in point P.

In the plane model of the classical Laguerre plane is the real affine plane . In general: ${\displaystyle {\mathcal {A}}_{(\infty ,0)}}$ ${\displaystyle \mathbb {R} ^{2}}$

• Every derivative of a Laguerre plane is an affine plane .

This results in the alternative definition of a Laguerre level (see Möbius level):

Theorem: An incidence structure together with an equivalence relation of is a Laguerre plane if and only if the derivative is an affine plane for every point . ${\displaystyle \parallel }$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle P}$ ${\displaystyle {\mathcal {A}}_{P}}$

Finite Laguerre plains

Minimal model of a Laguerre plane (only 4 of 8 cycles are drawn)

The following incidence structure is a minimal model of a Laguerre plane:

${\displaystyle {\mathcal {P}}:=\{A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}\},\quad {\mathcal {Z}}:=\{\{A_{i},B_{j},C_{k}\}\ |\ i,j,k=1,2\}}$,

${\displaystyle A_{1}\parallel A_{2},\ B_{1}\parallel B_{2},\ C_{1}\parallel C_{2}.}$.

So is and ${\displaystyle |{\mathcal {P}}|=6}$ ${\displaystyle |{\mathcal {Z}}|=8.}$

For finite Laguerre planes, i.e. H. , surrendered: ${\displaystyle |{\mathcal {P}}|<\infty }$

• For every cycle and every generating line of a finite Laguerre plane : ${\displaystyle z_{1},z_{2}}$ ${\displaystyle {\overline {P}}}$ ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$

${\displaystyle |z_{1}|=|z_{2}|=|{\overline {P}}|+1}$.

For a finite Laguerre plane and a cycle the natural number is called the order of . ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ ${\displaystyle z\in {\mathcal {Z}}}$ ${\displaystyle n:=|z|-1}$ ${\displaystyle {\mathcal {L}}}$

From combinatorial considerations it follows:

• It is a Laguerre level of order . Then: ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )}$ ${\displaystyle n}$

a) Every derivative is an affine plane of order b) c) ${\displaystyle {\mathcal {A}}_{P}}$ ${\displaystyle n\quad ,}$ ${\displaystyle |{\mathcal {P}}|=n^{2}+n\quad ,}$ ${\displaystyle |{\mathcal {Z}}|=n^{3}.}$

The classic real Laguerre plain

Originally, the classical real Laguerre plane was defined as the geometry of directed circles and straight lines in the Euclidean plane. For a better comparison with a Möbius plane (geometry of the circles) and a Minkowski plane (geometry of the hyperbolas), we prefer the parabolic model here.

We define:

${\displaystyle {\mathcal {P}}:=\mathbb {R} ^{2}\cup (\{\infty \}\times \mathbb {R} ),\ \infty \notin \mathbb {R} ,}$be the set of points ,

${\displaystyle {\mathcal {Z}}:=\{\{(x,y)\in \mathbb {R} ^{2}\mid y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\mid a,b,c\in \mathbb {R} \}}$be the set of cycles .

The point set is plus one copy of the real numbers (see picture). Each parabola / straight line receives the additional point . ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle y=ax^{2}+bx+c}$ ${\displaystyle (\infty ,a)}$

Two points with the same x-coordinate cannot be connected by cycles and are called parallel ( ). So: ${\displaystyle A,B}$ ${\displaystyle A\parallel B}$

• Two points are parallel if and only if is. is an equivalence relation , similar to the parallelism of straight lines. ${\displaystyle (a_{1},a_{2}),(b_{1},b_{2})}$ ${\displaystyle a_{1}=b_{1}}$ ${\displaystyle \parallel }$
• The incidence structure fulfills the axioms (B1), (B2), (B3) and (B4) and is called the classical real Laguerre plane . ${\displaystyle ({\mathcal {P}},{\mathcal {Z}},\in )}$

classic Laguerre level: 2d / 3d model

Similar to the spherical model of the classic Möbius plane, there is the cylinder model of the classic Laguerre plane:

• ${\displaystyle ({\mathcal {P}},{\mathcal {Z}},\in )}$ is isomorphic to the geometry of the plane sections of a circular cylinder.

The following illustration projects the xz-plane from the point onto the cylinder with the equation , axis and radius ${\displaystyle \Phi }$ ${\displaystyle (0,1,0)}$ ${\displaystyle u^{2}+v^{2}-v=0}$ ${\displaystyle (0,{\tfrac {1}{2}},\dots )}$ ${\displaystyle r={\tfrac {1}{2}}\ :}$

${\displaystyle \Phi :\ (x,z)\rightarrow \left({\frac {x}{1+x^{2}}},{\frac {x^{2}}{1+x^{2}}},{\frac {z}{1+x^{2}}}\right)=(u,v,w)\ .}$

• The points (straight line through the center) have no archetypes. ${\displaystyle (0,1,a)}$
• ${\displaystyle \Phi }$projects the parabola / straight line with the equation into the plane . I.e. the image of the parabola / straight line is the intersection of a non-perpendicular plane with the cylinder and thus a circle / ellipse without the point . The parabolas / straight lines are mapped onto (horizontal) circles. ${\displaystyle z=ax^{2}+bx+c}$ ${\displaystyle w-a=bu+(a-c)(v-1)}$ ${\displaystyle (0,1,a)}$ ${\displaystyle z=ax^{2}+a}$
• A straight line (i.e. ) merges into a circle / ellipse through the projection center and a parabola (i.e. ) into a circle / ellipse does not . ${\displaystyle a=0}$ ${\displaystyle (0,1,0)}$ ${\displaystyle a\neq 0}$ ${\displaystyle (0,1,0)}$

Miquelian Laguerre Plains

In contrast to Möbius planes, the replacement of the real numbers in the classical model of a Laguerre plane by any body always leads to a Laguerre plane. ${\displaystyle \mathbb {R} }$ ${\displaystyle K}$

Sentence: For a body and ${\displaystyle K}$

${\displaystyle {\mathcal {P}}:=K^{2}\cup }$ ${\displaystyle (\{\infty \}\times K),\ \infty \notin K}$,

${\displaystyle {\mathcal {Z}}:=\{\{(x,y)\in K^{2}\ |\ y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\ |\ a,b,c\in K\}}$ is the incidence structure

${\displaystyle {\mathcal {L}}(K):=({\mathcal {P}},{\mathcal {Z}},\in )}$a Laguerre plane with the following parallelism relation: if and only if is. ${\displaystyle (a_{1},a_{2})\parallel (b_{1},b_{2})}$ ${\displaystyle a_{1}=b_{1}}$

As with Mobius levels levels Laguerre applies for the set of Miquel in the following on Laguerre planes adapted version: ${\displaystyle {\mathcal {L}}(K)}$

Miquel's theorem (circles instead of parabolas)

Theorem ( MIQUEL ): The following applies to the Laguerre level : ${\displaystyle {\mathcal {L}}(K)}$

If for any 8 points pairs of non-parallel points , which can be assigned to the corners of a cube in such a way that 4 points with 5 faces each lie on a cycle, this is also the case for the 4 points on the 6th face (see Sect. Image: For a better overview, circles were drawn instead of parabolas). ${\displaystyle P_{1},\dots ,P_{8}}$

The meaning of Miquel's theorem is shown in the following theorem by vd Waerden, Smid and Chen:

Theorem ( vd Waerden , Smid, Chen ): Only one Laguerre plane fulfills Miquel's theorem. ${\displaystyle {\mathcal {L}}(K)}$

Because of this theorem, a Miquelian is called Laguerre plane . ${\displaystyle {\mathcal {L}}(K)}$

Comment:

1. The minimal model of a Laguerre plane is Miquelian: it is isomorphic to the Laguerre plane with (body ). ${\displaystyle {\mathcal {L}}(K)}$ ${\displaystyle K=GF(2)}$ ${\displaystyle \{0,1\}}$
2. The proof of Miquel's theorem for a Laguerre plane uses the peripheral angle theorem for parabolas (see parabola ) and is carried out analogously to the proof of Miquel's theorem for circles / straight lines in the real case. ${\displaystyle {\mathcal {L}}(K)}$
3. A suitable stereographic projection (see above) shows: is isomorphic to the geometry of the plane sections of a cylindrical quadric above the body . ${\displaystyle {\mathcal {L}}(K)}$ ${\displaystyle K}$

Laguerre Ovoid Plains

There are many Laguerre plains that are not miquelian (see web link). A large class of Laguerre plains containing the miquelian form the ovoid Laguerre plains. An Ovoid Laguerre Plane is the geometry of the plane cuts on an oval cylinder. An oval cylinder is a square set and has the same geometric properties as a circular cylinder in real 3-dimensional space: The cross section is an oval and an oval is a flat set of points with the following properties: 1) A straight line meets an oval in 0.1 or 2 points, 2) There is exactly one tangent at each point. In the real plane one can e.g. B. smoothly connect a semicircle with one half of an ellipse in a suitable manner to obtain an oval that is not a quadric. Even in the finite case there are ovals that are not quadrics (see quadratic set). For the class of ovoidalen Laguerre levels, there is a set of the Miquel similar lock set, the bundle theorem (ger .: Bundle Theorem ). It characterizes the ovoid Laguerre plains. Miquel's theorem and the Büschels theorem have a similar meaning for Laguerre planes as the Pappos and Desargues theorems have for projective planes.

Individual evidence

1. ^ Walter Benz : Lectures on the geometry of algebras . Reprint from 1973. Springer , Heidelberg 2013, ISBN 978-3-642-88671-3 , p. 20 .
2. ^ Walter Benz : Lectures on the geometry of algebras . Reprint from 1973. Springer , Heidelberg 2013, ISBN 978-3-642-88671-3 , p. 11 .
3. ^ Walter Benz : Lectures on the geometry of algebras . Reprint from 1973. Springer , Heidelberg 2013, ISBN 978-3-642-88671-3 , p. 26 .
4. ^ Walter Benz: Lectures on the geometry of algebras . Reprint from 1973. Springer, Heidelberg 2013, ISBN 978-3-642-88671-3 , p. 11 .
5. ^ Planar Circle Geometries, an Introduction to Moebius, Laguerre and Minkowski Planes. (PDF; 891 kB), p. 76.
6. ^ Planar Circle Geometries, an Introduction to Moebius, Laguerre and Minkowski Planes. (PDF; 891 kB), p. 78.

Web links

• Benz plane at SpringerLink
• Lecture Note Planar Circle Geometries , an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF; 891 kB)

literature

• Walter Benz: Lectures on the geometry of algebras . Reprint from 1973. Springer, Heidelberg 2013, ISBN 978-3-642-88671-3 . , P. 11
• F. Buekenhout (ed.), Handbook of Incidence Geometry , Elsevier (1995) ISBN 0-444-88355-X , p. 1343