Focal conic section

Focal conic sections: ellipse, hyperbola
A, C: main
vertex of the ellipse and focal points of the hyperbola E, F: focal points of the ellipse and vertex of the hyperbola

Focal conic sections: two parabolas
A: vertex of the red parabola and focal point of the blue parabola
F: focal point of the red parabola and vertex of the blue parabola

In geometry , focal conic sections are a pair of curves consisting of either

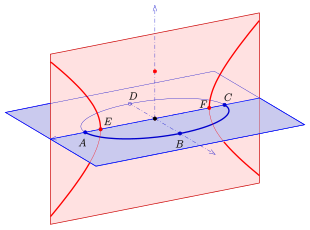
• an ellipse and a hyperbola , the hyperbola lying in a plane perpendicular to the plane of the ellipse and whose vertices are the focal points of the ellipse and whose focal points are the main vertices of the ellipse (see picture).

or

• two parabolas in mutually perpendicular planes, the vertex of one being the focal point of the other.

Focal conic sections result naturally when answering the question "Which cones of revolution contain a given ellipse, hyperbola or parabola as a section?" (See below)

They also play an essential role in geometry

1. in the generation of Dupin's cyclides . There they are guide curves for the representation of a cyclide as a channel surface .
2. in the thread construction of 3-axis ellipsoids .

In physical chemistry , focal conics are used to describe the geometric properties of liquid crystals .

One should not confuse focal conics with confocal conics . In the latter, all conic sections have the same focal points.

Equations and parametric representations

Ellipse and hyperbola

Equations

Describes the ellipse in the xy-plane as usual by the equation

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\;,}$

the associated focal hyperbola in the xz plane of the equation is sufficient

${\displaystyle {\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b^{2}}}=1\;,}$

where is the linear eccentricity of the ellipse, d. H. it applies ${\displaystyle c}$ ${\displaystyle \;c^{2}=a^{2}-b^{2}\;.}$

Parametric representations

Ellipse: and ${\displaystyle \quad {\vec {u}}(\varphi )=(a\cos \varphi ,b\sin \varphi ,0)^{T}\ }$

Hyperbole: ${\displaystyle \ {\vec {v}}(\psi )=(c\cosh \psi ,0,b\sinh \psi )^{T}\ .}$

Two parables

Two parabolas in the xy plane or xz plane:

1st parabola: and ${\displaystyle \ y^{2}=p^{2}-2px\ }$

2nd parabola: ${\displaystyle \ z^{2}=2px\ .}$

Where is the half parameter of the two parabolas. ${\displaystyle p}$

Circular cone (green) through an ellipse (blue)

Rotation cone through an ellipse or a hyperbola

• The tips of the cones of rotation through a given ellipse (hyperbola) lie on the focal hyperbola (focal ellipse) belonging to the ellipse (hyperbola).

above: cone of rotation (green, tip S) through the ellipse (blue),
k: Dandelin's sphere (purple, center point K)

proof

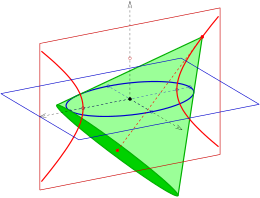
Given : an ellipse with main vertex and focal points and a cone of revolution containing the ellipse (green in the picture) with a tip . ${\displaystyle A,B}$ ${\displaystyle E,F}$ ${\displaystyle S}$

For reasons of symmetry, the axis of rotation of the cone must lie in the plane perpendicular to the plane of the ellipse through the main axis of the ellipse. There is a Dandelin sphere that touches the plane of the ellipse at the focal point and the cone in a circle. With the help of the picture and the fact that all tangential distances of a point from a sphere are the same, one recognizes: ${\displaystyle k}$ ${\displaystyle F}$

${\displaystyle |AS|=|AA_{1}|+|A_{1}S|=|AF|+|B_{1}S|}$

${\displaystyle |BS|=|BB_{1}|+|B_{1}S|=|BF|+|B_{1}S|}$

So is:

${\displaystyle |AS|-|BS|=|AF|-|BF|=|EF|=const.}$

and the set of all possible cone points lie on the hyperbola with the vertices and the focal points . ${\displaystyle S}$ ${\displaystyle E,F}$ ${\displaystyle A,B}$

If you let the cone tip wander into infinity, the cone turns into a cylinder with the asymptote of the hyperbola as the axis and with the small ellipse half-axis (= small hyperbola half-axis) as the radius.

Analogously one proves the case that a hyperbola is given.

Section of the cones through focal conic sections

Orthogonal cones (green, brown) through (purple) ${\displaystyle {\overline {ST}}}$

The perpendicular circular cones associated with a pair of focal conic sections through the conic sections (see previous section) play an important role in the application of Dupin's theorem to Dupin's cyclides. Because it applies

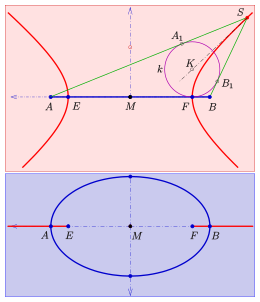
If one chooses any point of the hyperbola and any point of the ellipse and the circular cone (green) is through the ellipse with a tip and the circular cone (brown) through the hyperbola with a tip , then both cones intersect perpendicularly in the common straight line . ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle k_{S}}$ ${\displaystyle S}$ ${\displaystyle k_{T}}$ ${\displaystyle T}$ ${\displaystyle {\overline {ST}}}$

The key to the proof lies in the fact that the cone axis from is the tangent to the hyperbola in the point . The same applies: The axis of the cone is tangent to the ellipse in . Both statements follow from the fuel beam properties of an ellipse or hyperbola (see picture). ${\displaystyle a_{S}}$ ${\displaystyle k_{S}}$ ${\displaystyle S}$ ${\displaystyle a_{T}}$ ${\displaystyle k_{T}}$ ${\displaystyle T}$

Since we are dealing with vertical circular cylinders, it suffices to show that the normal planes of the cones intersect orthogonally: ${\displaystyle {\overline {ST}}}$

Is

${\displaystyle S:{\vec {s}}=(c\cosh \psi ,0,b\sinh \psi )^{T}\ }$and so is ${\displaystyle \ T:{\vec {t}}=(a\cos \varphi ,b\sin \varphi ,0)^{T}\ }$

${\displaystyle {\vec {s}}'=(c\sinh \psi ,0,b\cosh \psi )^{T}\ }$and . ${\displaystyle \ {\vec {t}}'=(-a\sin \varphi ,b\cos \varphi ,0)^{T}\ }$

The following applies: (see above). ${\displaystyle \ c^{2}=a^{2}-b^{2}\ }$

It has to be proven that the normal vectors of the two normal planes are perpendicular to one another, i.e. h. that

${\displaystyle ({\vec {s}}'\times ({\vec {s}}-{\vec {t}}))\cdot ({\vec {t}}'\times ({\vec {s}}-{\vec {t}}))=0\ }$ is.

When recalculating, one can avoid the cross product with the help of the Lagrange identity :

${\displaystyle ({\vec {s}}'\times ({\vec {s}}-{\vec {t}}))\cdot ({\vec {t}}'\times ({\vec {s}}-{\vec {t}}))=({\vec {s}}'\cdot {\vec {t}}')\;({\vec {s}}-{\vec {t}})^{2}-({\vec {t}}'\cdot ({\vec {s}}-{\vec {t}}))\;({\vec {s}}'\cdot ({\vec {s}}-{\vec {t}}))\ }$

literature

• Georg Glaeser, Hellmuth Stachel, Boris Odehnal: The Universe of Conics , Springer, 2016, ISBN 3662454505 .
• E. Müller, E. Kruppa : Textbook of the performing Geomelrie , Springer-Verlag, Vienna, 1961, ISBN 978-3-211-80589-3 .

Individual evidence

1. ↑ Müller-Kruppa, p. 104
2. ↑ Glaeser-Stachel-Odehnal, p. 137
3. ↑ Felix Klein: Lectures on Higher Geometry , editor: W. Blaschke, Richard Courant, Springer-Verlag, 2013, ISBN 3642498485 , p. 58.
4. ↑ Glaeser-Stachel-Odehnal: p. 147
5. ↑ D. Hilbert & S Cohn-Vossen: Illustrative Geometry , Springer-Verlag, 2013, ISBN 3662366851 , p. 18.
6. ↑ Thomas Andrew Waigh: The Physics of Living Processes , Verlag John Wiley & Sons, 2014, ISBN 1118698274 , p. 128.
7. ↑ Glaeser-Stachel-Odehnal p. 139