Dupin's cyclides

Ring cyclides with lines of curvature (circles)

In geometry, a Dupin's cyclid is a surface named after the French mathematician Charles Dupin with special geometric properties. The most outstanding feature is:

(KL) A Dupin's cyclide is covered by two vertically intersecting sets of circles. Each of these circles is a line of curvature .

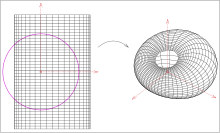
The simplest examples are the rotation gates and other toroidal surfaces (see picture).

Dupin's cyclides have been extensively studied not only by Dupin, but also by A. Cayley and JC Maxwell .

Today, Dupin's cyclides are of particular interest in the CAD area, as cyclic parts can be described by rational functions and are suitable for modeling smooth transitions between channel surfaces (cylinder, cone, tori ...).

Definition of a Dupin's cyclide

Dupin investigated surfaces whose lines of curvature are circles, and in 1822 in his book Applications de Geometrie gave the following definition of a class of such surfaces:

• The enveloping surface of a group of spheres, which 3 predetermined spheres touch in a continuous manner, is called (Dupin's) cyclide .

Further equivalent definitions and generalizations can be found in the literature.

Parametric representation, implicit representation

(KF) A Dupin's cyclide can be described in two ways as the enveloping surface of a single-parameter set of spheres, i.e. H. it is a channel surface and can be generated with two different guide curves. The guide curve pairs are focal conic sections and consist either of an ellipse and a hyperbola or two parabolas, the vertex of the ellipse being the focal point of the hyperbola and vice versa or the vertex of one parabola being the focus of the other and vice versa. In the first case one calls the cyclide elliptical in the second case parabolic . In both cases the conic sections lie in mutually perpendicular planes. In exceptional cases (if the ellipse is a circle) the hyperbola can degenerate into a straight line. The cyclide is then a torus of rotation.

The pair of guide curves is the focal surface of the cyclide that has degenerated into two curves .

Elliptical cyclides

An elliptical cyclide can be described by the following parameter representation (see section Cyclides as a channel surface ):

Meaning of the shape parameters . Here is: and is the radius of the generating sphere in the secondary vertices of the ellipse (see cyclid as channel surface ) The two vertical circles with the centers have the radii . ${\displaystyle a,b,c,d}$ ${\displaystyle a=1,\;b=0.98\to c=0.199}$ ${\displaystyle d=0.3}$
${\displaystyle d}$
${\displaystyle (\pm a,0,0)}$ ${\displaystyle d\mp c}$

${\displaystyle x={\frac {d(c-a\cos u\cos v)+b^{2}\cos u}{a-c\cos u\cos v}}\ ,}$

${\displaystyle y={\frac {b\sin u(a-d\cos v)}{a-c\cos u\cos v}}\ ,}$

${\displaystyle z={\frac {b\sin v(c\cos u-d))}{a-c\cos u\cos v}}\ ,}$

${\displaystyle 0\leq u,v<2\pi \ .}$

The numbers with are the major or minor semi-axis of an ellipse in the xy-plane and its linear eccentricity : ${\displaystyle a,b,c}$ ${\displaystyle \ a>b>0,\;c^{2}=a^{2}-b^{2}}$ ${\displaystyle c}$

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,\quad z=0\ .}$

The hyperbola

${\displaystyle {\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b^{2}}}=1,\quad y=0\;}$

in the xz plane is the focal conic section belonging to the ellipse, i.e. H. the foci of the ellipse are the vertices of the hyperbola and the vertices of the ellipse are the foci of the hyperbola. The two conic sections form the focal surfaces (here: focal lines) of the cyclides that have degenerated into two curves .

The number is a shape parameter of the cyclides. In the case of a ring cyclide, there is a mean radius of the spheres that create the cyclides as a channel surface. For a torus of revolution is the radius of the rotating circle. ${\displaystyle \;d\geq 0\ }$ ${\displaystyle d}$ ${\displaystyle d}$

For or you get the lines of curvature (circles) of the surface. ${\displaystyle u={\text{const.}}}$ ${\displaystyle v={\text{const.}}}$

The respective implicit representation is:

${\displaystyle (x^{2}+y^{2}+z^{2}+b^{2}-d^{2})^{2}-4(ax-cd)^{2}-4b^{2}y^{2}=0\ .}$

If is , i. H. the ellipse becomes a circle and the hyperbola degenerates into a straight line. The associated cyclides are then rotational gates. ${\displaystyle a=b}$ ${\displaystyle c=0}$

(ellipt.) Dupin's cyclids for shape parameters a, b, c, d
${\displaystyle d=0}$	${\displaystyle 0<d<c}$	${\displaystyle d=c}$	${\displaystyle c<d}$	${\displaystyle d=a}$	${\displaystyle a<d}$
symm. Horn cyclides	Horn cyclides	Unicorn cyclides	Ring cyclides	Ring cyclides	Spindle cyclides

The intersection points of the cyclides with the x-axis are more intuitive than the shape parameters . See also the section Cyclids through 4 points on the x-axis . ${\displaystyle a,b,c,d}$

Parabolic cyclides

A parabolic cyclide can be described by the following parameter representation (see section Cyclides as channel surface ):

parabolic cyclides with guide parabolas

${\displaystyle x={\frac {p}{2}}\,{\frac {2v^{2}+k(1-u^{2}-v^{2})}{1+u^{2}+v^{2}}}\ ,}$

${\displaystyle y=pu\,{\frac {v^{2}+k}{1+u^{2}+v^{2}}}\ ,}$

${\displaystyle z=pv\,{\frac {1+u^{2}-k}{1+u^{2}+v^{2}}}\ ,}$

${\displaystyle -\infty <u,v<\infty \ .}$

Having determined the shape of the two parabolas (Fokalkegelschnitte): ${\displaystyle p}$

${\displaystyle y^{2}=p^{2}-2px,\ z=0\ }$ (red in the picture) and

${\displaystyle z^{2}=2px,\ y=0\ }$ (blue).

(For the geometric meaning of : see parabola ). The shape parameter defines the diameter of the horizontal hole in multiples of . For both holes have the same diameter. In the picture is . ${\displaystyle p}$ ${\displaystyle k}$ ${\displaystyle p/2}$ ${\displaystyle k=0.5}$ ${\displaystyle k=0.7}$

A related implicit representation is

${\displaystyle \left(x+\left({\frac {k}{2}}-1\right)p\right)\left(x^{2}+y^{2}+z^{2}-{\frac {k^{2}p^{2}}{4}}\right)+pz^{2}=0\ .}$

parabolic Dupin's cyclides for design parameters p = 1, k
${\displaystyle k=0{,}5}$	${\displaystyle k=1}$	${\displaystyle k=1{,}5}$
Ring cyclides	Unicorn cyclides	Zweihorn cyclides

Note : The gaps in the representation of the circles are caused by the necessary restriction of the parameters . ${\displaystyle u,v}$

Cyclides as a channel surface

Dupin's cyclides as a channel surface (envelope of a spherical array)

In the book Analytical Geometry , Wilhelm Blaschke gives the following two constructions of a cyclide as a channel surface :

Ellipse as a guide curve

In the xy plane is the ellipse with the equation

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\ ,\ z=0}$

given as a leading curve. It has the parametric representation ${\displaystyle a>b}$

${\displaystyle \ x=a\cos \varphi \;,\ y=b\sin \varphi \;,\ z=0\ .}$

It is the great and the small semi-axis of the ellipse. The following is the linear eccentricity of the ellipse, i.e. H. it is . The radii of the generating spheres are ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle c^{2}=a^{2}-b^{2}}$

${\displaystyle r(\varphi )=d-c\cos \varphi \ .}$

${\displaystyle d}$is a shape parameter. It can be seen as a mean sphere radius. In the case , the ellipse is a circle and the cyclide is a torus of rotation with a small radius . ${\displaystyle c=0}$ ${\displaystyle d}$

In the picture is . ${\displaystyle \;a=1,\;b=0.99,\ d=0.25\;}$

Property of the focal points of the guide ellipse. The ellipse is the equidistant curve of the blue and purple circles.

Property of Maxwell

The following simple relationship between the respective center point of the sphere (ellipse point) and the associated sphere radius goes back to Maxwell:

• The sum of the radius of the sphere and the distance between the center of the sphere (point of the ellipse) and one of the two fixed focal points of the guide ellipse is constant.

proof

The foci of the above ellipse are . If you select and calculate the distance , this results . With the above sphere radius is . If you choose the other focal point, the result is ${\displaystyle \ E=(a\cos \varphi ,b\sin \varphi ,0)\ }$ ${\displaystyle \ F_{i}=(\pm c,0,0)\ }$ ${\displaystyle \ F_{1}=(c,0,0)\ }$ ${\displaystyle \ |EF_{1}|\ }$ ${\displaystyle \ |EF_{1}|=a-c\cos \varphi \ }$ ${\displaystyle \ |EF_{1}|-r=a-d\ }$
${\displaystyle \ |EF_{2}|+r=a+d\ .}$

Ie: In the xy plane, the envelopes of the spherical circles are two circles with the focal points of the guide ellipse as the center and the radii (see picture). ${\displaystyle a\pm d}$

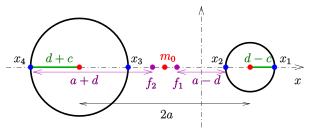
Cyclides through 4 points on the x-axis

To determine the shape parameters a, b, c, d as specified by ${\displaystyle x_{1},x_{2},x_{3},x_{4}}$

Above: ring cyclides with middle: horn cyclides with below: spindle cyclides with ${\displaystyle x_{1}=3,x_{2}=1,x_{3}=-3,x_{4}=-7}$
${\displaystyle x_{1}=1,x_{2}=3,x_{3}=-3,x_{4}=-7}$
${\displaystyle x_{1}=3,x_{2}=-3,x_{3}=1,x_{4}=-7}$

The Maxwell property makes it possible to define a ring cyclic symmetrical to the xz-plane and xy-plane by specifying its intersection points on the x-axis:

Given: four points on the x-axis (see picture). ${\displaystyle x_{1},x_{2},x_{3},x_{4}}$

Wanted: center point , semi-axes , linear eccentricity and focal points of the guide ellipse as well as the mean radius of the ring cyclides. ${\displaystyle m_{0}}$ ${\displaystyle a,b}$ ${\displaystyle c}$ ${\displaystyle d}$

First of all, the Maxwell properties result

${\displaystyle 2(a+d)=x_{1}-x_{4}\;,\quad \ 2(a-d)=x_{2}-x_{3}\ }$

and it

${\displaystyle a={\frac {1}{4}}\left(x_{1}+x_{2}-x_{3}-x_{4}\right),\quad }$ ${\displaystyle d={\frac {1}{4}}\left(x_{1}-x_{2}+x_{3}-x_{4}\right)\ .}$

The position of the focal points (on the x-axis) is

${\displaystyle f_{1}={\frac {1}{2}}(x_{2}+x_{3}),\quad f_{2}={\frac {1}{2}}(x_{1}+x_{4})}$ and thus

${\displaystyle c={\frac {1}{4}}\left(-x_{1}+x_{2}+x_{3}-x_{4}\right)\;,\quad \ b={\sqrt {a^{2}-c^{2}}}\ }$

The center of the focal conic sections is included

${\displaystyle m_{0}={\frac {1}{4}}\left(x_{1}+x_{2}+x_{3}+x_{4}\right)\ .}$

When using the above parameter representation, the center shifted here must be taken into account!

Importance of the arrangement of ${\displaystyle x_{1},x_{2},x_{3},x_{4}}$

(H) If you mix up the example , a horn cyclide is created. (S) If you swap, you get a spindle cyclide. (E) If one sets a unicorn cyclide. (R) If you set , you get a ring cyclide touching at the zero point. ${\displaystyle x_{1},x_{2}}$
${\displaystyle x_{2},x_{3}}$
${\displaystyle x_{1}=x_{2}=2}$
${\displaystyle x_{2}=x_{3}=0}$

Parallel surfaces

Parallel surfaces of a cyclide with parameters ${\displaystyle a=1,b=0.98,\ d=0.30,0.45,0.60}$

If the parameter is enlarged or reduced in such a way that no new types (horn cyclides ...) are created, parallel surfaces are obtained (analogous to parallel curves) , which are again cyclides (see picture). ${\displaystyle d}$

Hyperbola as a guide curve

The book also describes the second generation of the cyclid as a canal surface with the centers on the focal hyperbola belonging to the above ellipse. The equation of the hyperbola is

Cyclides with two spheres of contact, the centers of which lie on the focal hyperbola

${\displaystyle {\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b^{2}}}=1\ ,\ y=0\ .}$

In this case, the spheres touch the cyclides from outside in the second set of circles. A subset of spheres belongs to each branch of the hyperbola. The spheres of one group enclose the cyclid (in the picture: purple sphere). The other group is touched from the outside by the cyclide (in the picture: blue).

The hyperbola has the parametric representation

${\displaystyle (\pm c\cosh \psi ,0,b\sinh \psi )\ .}$

The radii of the associated spheres are

${\displaystyle R(\psi )=a\cosh \psi \mp d\ .}$

In the torus case ( ) the hyperbola degenerates into the torus axis. ${\displaystyle c=0}$

Maxwell property for hyperbola. The hyperload is also the equidistance curve of the two gray circles. ${\displaystyle H_{+}}$

Maxwell property for hyperbola

The focal points of the hyperbola are . For the distance of the hyperbolic point from the focal point we finally get and with the spherical radius . Analogously results . For a point on the second branch we get: ${\displaystyle \;H_{\pm }(\psi )=(\pm c\cosh \psi ,0,b\sinh \psi )\;}$ ${\displaystyle \;F_{i}=(\pm a,0,0)\;}$ ${\displaystyle \;H_{+}(\psi )=(c\cosh \psi ,0,b\sinh \psi )\;}$ ${\displaystyle F_{1}}$ ${\displaystyle \;|H_{+}F_{1}|=a\cosh \psi -c\;}$ ${\displaystyle R_{+}(\psi )=a\cosh \psi -d}$ ${\displaystyle \;|H_{+}F_{1}|-R_{+}=d-c\;}$ ${\displaystyle \;|H_{+}F_{2}|-R_{+}=d+c\;}$ ${\displaystyle \;R_{-}-|H_{-}F_{1}|=d-c\;,\ R_{-}-|H_{-}F_{2}|=d+c\;.}$

That means: In the xz-plane the circles (intersections of the spheres with the xz-plane) with the centers and radii envelop the two circles (gray in the picture) with centers and radii . ${\displaystyle H_{\pm }(\psi )}$ ${\displaystyle R_{\pm }(\psi )}$ ${\displaystyle F_{1/2}=(\pm a,0,0)}$ ${\displaystyle d\mp c}$

Point construction

Derivation of the parametric representation

Elliptical cyclides

The ellipse and the hyperbola are the focal surfaces that have degenerated into a pair of curves (here: focal lines) of the cyclides clearly determined by them and the parameter . If an arbitrary pair of points is the ellipse and the hyperbola, then (because of the property of focal surfaces): ${\displaystyle d}$ ${\displaystyle E,H}$

1) the straight line is a normal of cyclides and ${\displaystyle {\overline {EH}}}$

2) the associated cyclic point divides the distance in the ratio of the associated spherical radii . ${\displaystyle EH}$ ${\displaystyle r,R}$

With parametric display and spherical radius of the

ellipse ${\displaystyle \quad \ \ \ E(u)=(a\cos u,b\sin u,0),\quad r(u)=d-c\cos u\ \ ,}$

hyperbole ${\displaystyle \quad H(v)=({\frac {c}{\cos v}},0,b\tan v),\quad R(u)={\frac {a}{\cos v}}-d\ .}$

(For the somewhat unusual, but more suitable, parametric representation of the hyperbola, see: Hyperbola .)

you get the corresponding cyclic point (see picture):

${\displaystyle \ P(u,v)={\frac {R(v)}{r(u)+R(v)}}\;E(u)+{\frac {r(u)}{r(u)+R(v)}}\;H(v)\ .}$

The result is the parametric representation of an elliptical cyclide given above .

If you parameterize the cyclides as it is described in the article for channel surfaces, there is generally only a family of parameter curves made up of circles.

To describe the spherical radii

In order to avoid case distinctions, only the case is considered here. The other cases are analogous: ${\displaystyle 0\leq u,v<{\tfrac {\pi }{2}}}$

Since the centers of curvature are, it must apply (see picture) ${\displaystyle E(u),H(v)}$

${\displaystyle r(u)+R(v)=|E(u)H(v)|=\cdots ={\frac {a}{\cos v}}-c\cos u\ .}$

So it is and with any number . ${\displaystyle \ r(u)=d-c\cos u\ }$ ${\displaystyle \ R(v)={\frac {a}{\cos v}}-d\ }$ ${\displaystyle d}$

The parameter lines are circles

If there is, there is a perpendicular circular cone that contains the ellipse and has the point as its apex (see the article Focal Conic Section ). The sphere with as the center and as the radius cuts a circle, the parameter line , from the cone . Analogously it follows that there is a circle. ${\displaystyle v=v_{0}}$ ${\displaystyle H(v_{0})}$ ${\displaystyle H(v_{0})}$ ${\displaystyle R(v_{0})}$ ${\displaystyle P(u,v_{0})}$
${\displaystyle P(u_{0},v)}$

The circles are lines of curvature

To do this one proves:

(KO) If E, H are two points of the ellipse or hyperbola, the associated circular cones with point E and H intersect perpendicularly through the hyperbola or ellipse (see previous paragraph) along the common straight line EH.

Since the straight line EH is the normal in the cyclic point P lying on it, the two cones and the cyclic line intersect orthogonally in pairs in P. According to Dupin's theorem on triple orthogonal systems, the intersection curves (circles) with the cyclide are lines of curvature.

The statement (KO) is proven by showing that the normal planes of the cones through the straight line EH are perpendicular to one another. These planes go through EH and the respective cone axes (tangent of the ellipse in E or hyperbola in H, see focal conic section ).

Another proof: Every circle is the circle of contact of the cyclide with a sphere. Ie: all normals along a circle go through the center of the sphere. The normals thus form a torse (here a cone), which means that the circle is a line of curvature.

Parabolic cyclides

Generation of a parabolic cyclide as a channel surface

The derivation of the parametric representation for the parabolic case is analogous:

With the parametric representations and spherical radii of the guide parabolas (focal conic sections):

${\displaystyle P_{1}(u)=\left({\frac {p}{2}}(1-u^{2}),pu,0\right),\quad r_{1}={\frac {p}{2}}(1-k+u^{2})\;}$

${\displaystyle P_{2}(v)=\left({\frac {p}{2}}v^{2},0,pv\right),\qquad \qquad r_{2}={\frac {p}{2}}(k+v^{2})\ }$

results with

${\displaystyle \ P(u,v)={\frac {r_{2}(v)}{r_{1}(u)+r_{2}(v)}}\;P_{1}(u)+{\frac {r_{1}(u)}{r_{1}(u)+r_{2}(v)}}\;P_{2}(v)}$

the parametric representation above.

Dupin's cyclides and inversions

For investigations of the areas it is advantageous:

(I) Every Dupin's cyclid is the image of a vertical circular cylinder or a vertical circular cone or a torus of rotation under an inversion (reflection on a sphere).

The reflection ( inversion ) on the sphere with the equation can be described in analogy to the mirroring of a circle by: ${\displaystyle x^{2}+y^{2}+z^{2}=R^{2}}$

${\displaystyle (x,y,z)\rightarrow {\frac {R^{2}\cdot (x,y,z)}{x^{2}+y^{2}+z^{2}}}\ .}$

The most important properties of such a spherical reflection for cyclides are:

1. Balls and circles that do not contain the origin are mapped onto the same.
2. Planes / straight lines through the origin are mapped onto themselves.
3. Planes / straight lines that do not contain the origin are mapped to spheres / circles through the origin.
4. An inversion is involutive (identical to its reverse imaging).
5. An inversion is conformal.

Any surfaces can be represented with an inversion. The above mapping rule then immediately provides a parameter representation / implicit representation of the image area if the given area is parameterized / implicitly given. In the parameterized case:

${\displaystyle (x(u,v),y(u,v),z(u,v))\rightarrow {\frac {R^{2}\cdot (x(u,v),y(u,v),z(u,v))}{x(u,v)^{2}+y(u,v)^{2}+z(u,v)^{2}}}\ .}$

Ring cyclides by inversion of a cylinder on a sphere (magenta)

parabolic ring cyclides by inversion of a cylinder containing the zero point

Two-horn cyclides by inversion of a cone

Ring cyclides by inversion of a torus

But: only vertical circular cylinders, vertical circular cones and rotation gates are mapped onto Dupin's cyclides by inversion and vice versa.

Example cylinder

1. Since straight lines that do not contain the zero point are mapped to circles through the zero point when they are reflected on the sphere (in the picture: magenta), the image of the cylinder is a ring cyclide in which a group of circles touch at the zero point. Only circular arcs appear as images of routes. The spheres that touch the cylinder from the inside merge into the first set of spheres, which the cyclide creates as a channel surface from the outside. The tangential planes of the cylinder merge into the second set of spheres enveloping the cyclides from the inside. The latter balls all go through the origin.
2. In the second example, a surface line of the cylinder goes through the zero point. Straight lines through the zero point are mapped onto themselves. That is why the image is an unlimited surface, i.e. a parabolic cyclide.

Example cone

The surface lines of the cone are mapped onto circles that intersect at the zero point and in the image of the cone tip. The image of the cone is a two-horn cyclide. In the picture, the images of the mantle stretches only appear as arcs.

Ring cyclides with Villarceau circles

Example torus

The two sets of circles of the torus merge into the corresponding sets of circles of the ring cyclides. A rotating torus penetrating one another is mapped onto a spindle cyclide.
Villarceau circles form two more sets of circles on a torus. Since circles are usually mapped to circles again in the event of an inversion, there are also two further sets of circles on an inverted torus (see picture).

If, as with the Villarceau circles, the co-inverted torus circles are used for visualization, the point distribution of the circle network is not good. This can be improved by calculating the shape parameters and using the parametric representation introduced at the beginning: ${\displaystyle a,b,c,d}$

Cyclid (blue) by inversion of a torus (black) on the red unit sphere

Given: Torus that is shifted from the standard position in the x-direction. The sections with the x-axis have the x-values (see picture). All non-zero. Otherwise no ring cyclides will be produced. Wanted: semi-axes and linear eccentricity of Leitellipse and the mean radius (. S section parameter representation ) of the resulting in the inversion of the unit sphere of the torus Ringzyklide (blue in the picture). ${\displaystyle x_{1},x_{2},x_{3},x_{4}}$
${\displaystyle a,b}$ ${\displaystyle c}$ ${\displaystyle d}$

The Maxwell properties (see previous section) result

${\displaystyle a={\frac {1}{4}}\left({\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}-{\frac {1}{x_{4}}}\right),\quad }$ ${\displaystyle d={\frac {1}{4}}\left(-{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right)\ }$ and

${\displaystyle c={\frac {1}{4}}\left({\frac {1}{x_{1}}}-{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right)\;,\quad \ b={\sqrt {a^{2}-c^{2}}}\ }$

The center of the focal conic sections is included

${\displaystyle m_{0}={\frac {1}{4}}\left({\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+{\frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right)\ .}$

Web links

• mathcurve: cyclides
• L. Garnier, S. Foufou, M. Neveu: FROM DUPIN CYCLIDES TO SCALED CYCLIDES
• M. Peternell: Generalized Dupin Cyclides with Rational Lines of Curvature.
• E. Berberich, M. Kerber: Arrangements on Surfaces of Genus One: Tori and Dupin Cyclides.

literature

• A. Cayley: On the cyclide. In: Quarterly Journal of Pure and Applied Mathematics. 12, 1873, pp. 148-163.
• C. Dupin: Applications de Geometry et de Mechanique. Bachelier, Paris 1822.
• G. Fischer: Mathematical models: From the collections of universities and museums. Akademie-Verlag, 1986, ISBN 978-3-322-85046-1 , p. 30.
• K. Fladt: Analytical geometry of special surfaces and space curves. Vieweg-Teubner-Verlag, ISBN 978-3-528-08278-9 , p. 201.
• G. Glaeser: Geometry and its applications in art and technology. Springer-Verlag, 2014, ISBN 978-3-642-41851-8 , p. 229.
• D. Hilbert, S. Cohn-Vossen: Illustrative geometry. Springer-Verlag, 2011, ISBN 978-3-642-19947-9 , p. 192.
• F. Klein, W. Blaschke: Lectures on higher geometry. Springer-Verlag, 1926, ISBN 978-3-642-98494-5 , p. 56.
• JC Maxwell: On the cyclide. In: Quarterly Journal of Pure and Applied Mathematics. 9, 1868, pp. 111-126.
• MJ Pratt: Cyclide Blending in Solid Modeling. In: Wolfgang Strasser, Hans-Peter Seidel (Ed.): Theory and Practice in Geometric Modeling. Springer-Verlag, 1989, ISBN 0-387-51472-4 , p. 235.
• YL Srinivas, V. Kumar, D. Dutta: Surface design using cyclide patches. In: Computer-Aided Design. Volume 28, Issue 4, 1996, pp. 263-276.

Individual evidence

1. ↑ V. Chandru, D. Dutta, CM Hoffmann: On the geometry of Dupin cyclides. In: The Visual Computer. 1989 (5), pp. 277-290.
2. ^ W. Blaschke: Analytische Geometrie , Springer-Verlag, 2013, ISBN 303486812X , p. 115
3. ↑ mentioned in W. Boehm: On Cyclides in Geometric Modeling. Computer Aided Geometric Design 7, 1990, pp. 243-255.
4. ↑ s. Book by W. Blaschke
5. ↑ Blaschke, p. 61