Implicit area

implicit area torus (R = 40, a = 15)

implicit area of ​​gender 2

implicit non-algebraic surface ( wine glass )

An implicit surface in mathematics is a surface in Euclidean space that is represented by an equation of the form

${\displaystyle F(x,y,z)=0}$

is described. An implicit area consists of the totality of the zeros of a function of three variables. Implicit means that the equation of the area is not solved for x or y or z.

Function graphs are usually described by an equation and are therefore explicitly represented areas. The third important description of surfaces is the parameter representation: . The x, y and z coordinates of surface points are described by three functions that depend on two common parameters . The transition from one representation to another is usually only easy if there is an explicit representation : (implicit), (parameterized). ${\displaystyle z=f(x,y)}$ ${\displaystyle (x(s,t),y(s,t),z(s,t))}$ ${\displaystyle x(s,t)\,,y(s,t)\,,z(s,t)}$ ${\displaystyle z=f(x,y)}$ ${\displaystyle z-f(x,y)=0}$ ${\displaystyle (s,t,f(s,t))}$

Examples of implicit surfaces:

1. one level , ${\displaystyle x+2y-3z+1=0}$
2. a ball , ${\displaystyle x^{2}+y^{2}+z^{2}-4=0}$
3. a torus , ${\displaystyle (x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0}$
4. Area of gender 2: (see picture), ${\displaystyle 2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0}$
5. Surface of rotation (see picture wine glass ). ${\displaystyle x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0}$

While one can easily specify parametric representations for plane, sphere and torus, this is no longer easy for the fourth surface.

As with implicit curves , under certain conditions, the theorem on implicit functions can also be used to locally prove an explicit representation for implicit surfaces. In practice, such resolutions are only possible in simple cases (plane, sphere, ...). But the theoretical possibility of a resolution is the key to calculate tangent planes and curvatures in a surface point (see below).

If there is a polynomial in x, y and z, the associated area is called algebraic . ${\displaystyle F(x,y,z)}$

Example 5. is not algebraic.

Implicit areas have the disadvantage that they are difficult to visualize. However, they offer a wide range of theoretically interesting surfaces (e.g. Steiner surfaces ) and in the CAD area it is relatively easy to create surfaces with predictable shapes and properties (see below).

Formulas

For the following formulas, the implicit area is always described by an equation , whereby the function fulfills the necessary differentiability requirements. The partial derivatives of are denoted by etc. ${\displaystyle F(x,y,z)=0}$ ${\displaystyle F}$ ${\displaystyle F}$ ${\displaystyle F_{x},...,F_{xx},...}$

Tangent plane and normal vector

A surface point is called regular, if ${\displaystyle (x_{0},y_{0},z_{0})}$

• ${\displaystyle (F_{x}(x_{0},y_{0},z_{0}),F_{y}(x_{0},y_{0},z_{0}),F_{z}(x_{0},y_{0},z_{0}))\neq (0,0,0)}$is, otherwise the point is called singular .

The equation of the tangent plane in a regular surface point is ${\displaystyle (x_{0},y_{0},z_{0})}$

• ${\displaystyle F_{x}(x_{0},y_{0},z_{0})(x-x_{0})+F_{y}(x_{0},y_{0},z_{0})(y-y_{0})+F_{z}(x_{0},y_{0},z_{0})(z-z_{0})=0}$, and

${\displaystyle \mathbf {n} (x_{0},y_{0},z_{0})=(F_{x}(x_{0},y_{0},z_{0}),F_{y}(x_{0},y_{0},z_{0}),F_{z}(x_{0},y_{0},z_{0}))^{T}}$is a normal vector .

Normal curvature

In order to keep the formula clear, the arguments have been left out: ${\displaystyle (x_{0},y_{0},z_{0})}$

• ${\displaystyle \kappa _{n}={\frac {\mathbf {v} ^{\top }H_{F}\mathbf {v} }{\|\operatorname {grad} F\|}}}$is the normal curvature of the surface at a regular point in the direction of the unit tangent vector . ${\displaystyle \mathbf {v} }$

${\displaystyle H_{F}}$is the Hessian matrix of (matrix of the second derivatives). ${\displaystyle F}$

The proof of these formulas results, as in the case of the implicit curve, from the theorem about the resolution of implicit functions and the formula for the normal curvature of a parameterized surface.

Applications of implicit surfaces

Implicit surfaces, like implicit curves, can be generated relatively easily by algebraic operations (addition, multiplication) of simple implicit surfaces / functions.

Equipotential area of ​​4 point charges

Equipotential areas of point charges

The potential of a point charge in the point , measured in the point , can be passed through, except for constants ${\displaystyle q_{i}}$ ${\displaystyle \mathbf {p} _{i}=(x_{i},y_{i},z_{i})}$ ${\displaystyle \mathbf {p} =(x,y,z)}$

${\displaystyle F_{i}(x,y,z)={\frac {q_{i}}{\|\mathbf {p} -\mathbf {p} _{i}\|}}}$ describe.

The equipotential area to the potential is the implicit area . This is a centered sphere . ${\displaystyle c}$ ${\displaystyle F_{i}(x,y,z)-c=0}$ ${\displaystyle \mathbf {p} _{i}}$

The potential of (e.g.) point charges can be passed through ${\displaystyle 4}$

${\displaystyle F(x,y,z)={\frac {q_{1}}{\|\mathbf {p} -\mathbf {p} _{1}\|}}+{\frac {q_{2}}{\|\mathbf {p} -\mathbf {p} _{2}\|}}+{\frac {q_{3}}{\|\mathbf {p} -\mathbf {p} _{3}\|}}+{\frac {q_{4}}{\|\mathbf {p} -\mathbf {p} _{4}\|}}}$ describe.

In the figure the four charges are equal to 1 and are located in the points . The area shown is the equipotential area (implicit area) . ${\displaystyle (\pm 1,\pm 1,0)}$ ${\displaystyle F(x,y,z)-2.8=0}$

Constant spacing product areas

Just as a Cassinian curve can be defined as the set of points for which the product of the distances to two given points is constant (in an ellipse the sums of the distances to two points are constant!), Areas can also be defined whose distance products allow given points are constant.

The surface shown in the picture Metamorphoses at the top left is created according to this principle: With

${\displaystyle F(x,y,z)={\sqrt {(x-1)^{2}+y^{2}+z^{2}}}\cdot {\sqrt {(x+1)^{2}+y^{2}+z^{2}}}\cdot {\sqrt {x^{2}+(y-1)^{2}+z^{2}}}\cdot {\sqrt {x^{2}+(y+1)^{2}+z^{2}}}}$

results in the area . ${\displaystyle F(x,y,z)-1.1=0}$

Metamorphosis between two implicit surfaces (torus and distance product surface)

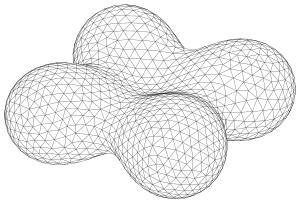
Metamorphoses of implicit surfaces

Another simple construction of new implicit surfaces is the metamorphosis of implicit surfaces. In doing so, one assumes two implicit surfaces (in the example: a distance product surface and a torus) and uses the array parameter to generate the array of surfaces ${\displaystyle F_{1}(x,y,z)=0,F_{2}(x,y,z)=0}$ ${\displaystyle \mu \in [0,1]}$

${\displaystyle F(x,y,z)=\mu F_{1}(x,y,z)+(1-\mu )F_{2}(x,y,z)=0}$

Areas for were shown in the picture. ${\displaystyle \mu =0,\,0.33,\,0.66,\,1}$

Approximation of three tori (parallel projection)

PovRay image of an approximation of three tori (central projection)

Smooth approximations of several implicit surfaces

Analogously to the method of the smooth approximation of several implicit curves,

${\displaystyle F(x,y,z)=F_{1}(x,y,z)\cdot F_{2}(x,y,z)\cdot F_{3}(x,y,z)-c=0}$

for suitable parameters, smooth approximations of three intersecting tori with the equations ${\displaystyle c}$

${\displaystyle F_{1}=(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0}$,

${\displaystyle F_{2}=(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+z^{2})=0}$,

${\displaystyle F_{3}=(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(y^{2}+z^{2})=0}$.

(The parameter of the face in the image are: ) ${\displaystyle R=1,\,a=0.2,\,c=0.01}$

PovRay image: metamorphosis between a sphere and a 6-point distance product surface

Visualization of implicit areas

Implicit areas can only be visualized with considerable effort. There are essentially two ideas for representing an implicit surface. One method is based on the generation of polygons that cover the area to be displayed. These polygons can be used directly to visualize the area or the polygons and their representation can be further processed with a suitable program. Information on this can be found in Triangulation of an Area. Another method is based on ray tracing . Here, many individual lines of sight are examined for their intersection with the surface.

In the last two images, the triangulated surfaces were post-processed with the PovRay program . When comparing the images with the 3 Tori, note that the PovRay image is a central projection.

Web links

• Sultanov: Implicit areas
• Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN
• GEOMVIEW
• K3Dsurf: 3d surface generator
• SURF: visualization of algebraic surfaces

literature

• John A. Thorpe: Elementary Topics in Differential Geometry. Springer-Verlag, New York 1979, ISBN 0-387-90357-7 .