Ray tracing
Ray tracing (dt. Ray tracing or ray tracing , in English spelling usually ray tracing ) is on the emission of radiation -based algorithm for concealment calculation , that is, from to determine the visibility of three-dimensional objects from a particular point in space. Ray tracing is also used to describe several extensions of this basic method, which calculate the further path of rays after they hit surfaces.
Ray tracing is most prominently used in 3D computer graphics . Here, the basic ray tracing algorithm is one way of representing a 3D scene . Extensions that simulate the path of light rays through the scene, like the radiosity method, are used to calculate the light distribution.
Other areas of application for ray tracing are auralization and high frequency technology .
Origin and meaning
Before ray tracing was developed, the young field of 3D computer graphics essentially consisted of a series of "programming tricks" designed to mimic the shading of illuminated objects. Ray tracing was the first algorithm in the field that made some physical sense.
The first ray- traced image was displayed on an oscilloscope-like screen at the University of Maryland in 1963 . Arthur Appel , Robert Goldstein and Roger Nagel , who published the algorithm in the late 1960s, are often considered to be the developers of the ray tracing algorithm . Other researchers studying ray tracing techniques at the time were Herb Steinberg , Marty Cohen, and Eugene Troubetskoy . Ray tracing is based on geometric optics , in which the light is understood as a group of rays. The techniques used in ray tracing were used much earlier by manufacturers of optical systems , among others . Today, many renderers (computer programs for generating images from a 3D scene) use ray tracing, possibly in combination with other methods.
Simple forms of ray tracing only calculate the direct lighting, i.e. the light arriving directly from the light sources. However, ray tracing has expanded significantly several times since it was first used in computer graphics. More developed shapes also take into account the indirect light reflected from other objects; one then speaks of a global lighting method .
The term raycasting usually denotes a simplified form of ray tracing, but is sometimes also used synonymously.
Basic principle
The creation of a raster image from a 3D scene is called rendering or image synthesis . Such a scene is first created by the user using a 3D modeling tool .
At least the following data are given in the scene description:
- the position of the elementary primitives such as polygons or spheres that make up the objects of the scene;
- the local lighting models and their parameters, which determine the colors and materials of the individual objects in the scene;
- the light sources of the scene.
In addition, with ray tracing, the position of an eye point and an image plane are specified, which together indicate the perspective from which the scene is viewed. The eye point is a point in space that corresponds to the position of a virtual camera or a general observer. The image plane is a virtual rectangle that is some distance from the eye point. It is the three-dimensional equivalent of the raster image to be rendered in space. Points distributed in grid form on the image plane correspond to the pixels of the raster image to be generated.
Occlusion calculation

Ray tracing is primarily a method for calculating occlusion , i.e. for determining the visibility of objects from the eye point. The basic principle is pretty simple.
Ray tracing works with a data structure called a ray that specifies the starting point and the direction of a half-line in space. For each pixel the direction of the ray is calculated, which points from the eye point to the corresponding pixel of the image plane. For each primitive of the scene, the possible intersection point at which the ray hits the primitive is determined by means of a geometric process . If necessary, the distance from the eye point to the intersection point is calculated. The “winner”, ie the primitive visible from the eye point, is the one with the smallest distance.
The principle of the emission of the rays from the eye point is similar to the structure of a pinhole camera in which an object is shown on a film. With ray tracing, however, “film” (image plane) and “hole” (eye point) are swapped. Similar to the pinhole camera, the distance between the image plane and the eye point determines the " focal length " and thus the field of view .
Since the rays do not emanate from the light sources, as in nature, but from the eye point, one also speaks of backward ray tracing . Ray tracing deals with the question of where the light comes from. However, some publications call the process forward ray tracing or eye ray tracing.
Intersection tests
The above-mentioned test for a possible intersection of ray and primitive is the heart of ray tracing. Such tests can be formulated for a variety of primitive types. In addition to triangles and spheres, cylinders , quadrics , point clouds or even fractals are possible.
For spheres, the intersection test is a relatively short and simple procedure, which explains the popularity of these objects on ray traced test images. For the sake of simplicity, however, many rendering programs only allow triangles as primitives, from which any object can be approximately composed.
More complex geometries such as NURBS have recently been used for the intersection test. A maximum of precision is advantageous here, since the surface is not divided into triangles as is usual. The disadvantage is an increased rendering time, since the intersection test with complex free-form surfaces is much more time-consuming than with simple triangles. A sufficient approximation to the accuracy of NURBS is also possible with triangles, but in this case a very large number must be selected.
Shading
When determining the next primitive, not only the point of intersection and its distance to the eye point, but also the normal of the primitive at the point of intersection is calculated. This means that all information is available to determine the “light intensity” reflected to the eye point and thus the color. The descriptions of the light sources in the scene are also used. The calculations are based on local lighting models that simulate the material properties of an object. This part of the renderer that is responsible for determining the color is called a shader .
Sample code
Programming a simple ray tracer requires little effort. The principle can be represented in pseudocode as follows:
Prozedur Bild_Rendern
Strahl.Ursprung := Augpunkt
Für jedes (x,y)-Pixel der Rastergrafik
Strahl.Richtung := [3D-Koordinaten des Pixels der Bildebene] − Augpunkt
Farbe des (x,y)-Pixels := Farbe_aus_Richtung(Strahl)
Funktion Farbe_aus_Richtung(Strahl)
Schnittpunkt := Nächster_Schnittpunkt(Strahl)
Wenn Schnittpunkt.Gewinner = (kein) dann
Farbe_aus_Richtung := Hintergrundfarbe
sonst
Farbe_aus_Richtung := Farbe_am_Schnittpunkt(Strahl, Schnittpunkt)
Funktion Nächster_Schnittpunkt(Strahl)
MaxDistanz := ∞
Schnittpunkt.Gewinner := (kein)
Für jedes Primitiv der Szene
Schnittpunkt.Distanz := Teste_Primitiv(Primitiv, Strahl)
Wenn Schnittpunkt.Distanz < MaxDistanz dann
MaxDistanz := Schnittpunkt.Distanz
Schnittpunkt.Gewinner := Primitiv
Nächster_Schnittpunkt := Schnittpunkt
Each raytracer, regardless of the raytracing variant used, follows a similar structure that also contains an intersection test ( Teste_Primitiv ) and a shader ( Farbe_am_Schnittpunkt ).
power
Acceleration techniques
When determining the first primitive that a ray hits, each primitive of the scene can be tested against the ray, as in the example code above. However, this is not fundamentally necessary if it is known that certain primitives are not in the vicinity of the ray anyway and therefore cannot be hit. Since intersection tests require the longest running time in ray tracing, it is important to test as few primitives as possible against the ray in order to keep the total running time low.
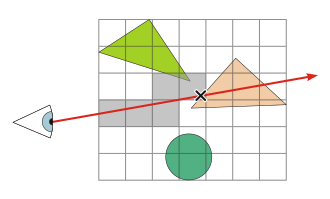
With the acceleration method, the scene is usually divided up automatically in some form and the primitives are assigned to these subdivisions. When a ray wanders through the scene, it is not tested against the primitives, but first against the subdivisions. This means that the ray only needs to be tested against the primitives of the subdivision that the ray crosses.
A variety of such acceleration techniques for ray tracing have been developed. Examples of subdivision schemes are voxel grids , BSP trees, and bounding volumes that enclose the primitives and form a hierarchy. Mixed forms of these techniques are also popular. There are also special acceleration techniques for animations . The complexity of these techniques allows a ray tracer to quickly grow into a larger project.
No technology is generally optimal; the efficiency depends on the scene. Nevertheless, every acceleration method reduces the running time enormously and makes ray tracing a practicable algorithm. Subdivisions based on Kd trees are the most efficient or almost most efficient technique for most non-animated scenes, as they can be optimized using heuristics . It has been found several times that the asymptotic runtime of ray tracing is logarithmic depending on the number of primitives .
It has been shown that on modern computers it is not the processor performance but rather memory access that limits the speed of ray tracing. Careful use of caching by the algorithm makes it possible to significantly reduce the runtime. It is also possible to use the SIMD capability of modern processors, which enable parallel calculations, as well as specially optimized subdivision schemes. This enables the simultaneous tracking of several rays combined in "packages". The reason for this is that the rays emitted by the eye point are usually very similar, i.e. they usually intersect the same objects. With the SSE instruction set, for example, four rays can be tested simultaneously for an intersection with a primitive, which speeds up this calculation many times over. On appropriate hardware implementations - for example on FPGAs - larger packets with over 1000 beams can also be tracked. However, caching and SIMD optimizations for advanced forms of ray tracing lose much of their speed advantage.
It is also possible to parallelize the entire ray tracing process . This can be achieved in a trivial way, for example, that different processors or machines render different sections of the image. Only certain acceleration techniques or extensions have to be adapted in order to be suitable for parallelization.
Memory requirements
The basic ray tracing method hardly requires any memory. However, the scene itself, which nowadays is often composed of several million primitives in complex scenes, occupies a great deal of memory and can comprise several gigabytes . Added to this is the more or less high additional memory requirement of the acceleration technologies. Since such large scenes do not completely fit into the computer's main memory , swapping is often necessary.
In the case of larger objects that appear several times in the scene and differ only in their position and size (e.g. in a forest full of trees), the entire geometry does not have to be saved again. This technique, called instancing , can save considerable space in certain scenes.
Extensions
One of the reasons for the success of ray tracing is its natural expandability. The primitive method described above is inadequate for today's requirements in image synthesis. With increasing computing power and increasing inspiration from physics - especially optics and radiometry - several extensions and variants emerged, some of which are briefly presented here.
Basically, with each expansion, the achievable quality of the rendered images as well as the relative time required increased sharply and reached the maximum with path tracing. Only subsequent developments were aimed at reducing the time required for path tracing without sacrificing quality.
shadow
Due to the flexibility of the ray tracing algorithm, it is possible to send light rays not only from the eye point, but also from any other point in space. As Arthur Appel demonstrated in 1968, this can be used to simulate shadows .
Any point on a surface is in shadow if and only if there is an object between it and the light source. By emitting a shadow beam from the point of intersection on the surface in the direction of the light source, it can be determined whether an object is crossing its path. If this is the case, the point of intersection is in the shadow and 0 is returned as the brightness of the ray. In the other case normal shading takes place.
Recursive ray tracing
Ray tracing can be applied not only to simple opaque objects , but also to transparent and specular, reflective objects. Additional light rays are emitted from the intersection points. In the case of reflective surfaces, for example, only the direction of the ray emanating from the surface needs to be taken into account in accordance with the law of reflection (angle of incidence equals reflection angle) and a corresponding reflection ray has to be calculated.
In the case of translucent objects, a beam is emitted according to Snellius' law of refraction , this time into the interior of the object in question. In general, transparent objects also reflect some of the light. The relative color components of the reflected and the refracted beam can be calculated using Fresnel's formulas . These rays are also called secondary rays .
Since the secondary rays can fall on other objects, the algorithm is called recursively in order to enable multiple reflections and light refractions. The hierarchical entirety of the calls is also called the rendering tree.
Recursive ray tracing was developed by Kay and Whitted around 1980.
In pseudocode , the shader for recursive ray tracing looks something like this:
Funktion Farbe_am_Schnittpunkt(Strahl, Schnittpunkt)
Wenn Schnittpunkt.Gewinner.Material = spiegelnd oder transparent dann
Reflektierter_Anteil := Fresnel(Strahl, Schnittpunkt)
Farbe := Reflektierter_Anteil × Farbe_aus_Richtung(Reflexionsstrahl)
+ Gebrochener_Anteil × Farbe_aus_Richtung(Gebrochener Strahl)
sonst
Farbe := 0
Für jede Lichtquelle
Schattenstrahl := Lichtquelle.Position - Schnittpunkt.Position
SchattenSchnittpunkt := Nächster_Schnittpunkt(Schattenstrahl)
Wenn SchattenSchnittpunkt.Gewinner = Lichtquelle dann
Farbe := Farbe + Direkte_Beleuchtung(Strahl, Lichtquelle)
Farbe_am_Schnittpunkt := Farbe
The rest of the program can remain as with simple ray tracing. The function Farbe_aus_Dichtung called here can in turn call Farbe_am_Schnittpunkt , from which the recursive character of the method becomes clear.
Diffuse ray tracing
In addition to refraction and reflection, recursive ray tracing enables the simulation of hard shadows. In reality, however, light sources are a certain size, which makes shadows appear soft and blurry.
This effect, as well as anti-aliasing , shiny reflection and more, can be simulated with diffuse ray tracing (also called stochastic ray tracing or distributed ray tracing ), which was developed by Cook et al. In 1984. a. has been published. The idea is to send out several rays instead of one ray in different situations and to calculate the mean value from the calculated colors. For example, soft shadows with umbra and penumbra can be created by randomly scanning the direction of the shadow rays across the surface of the light source. The disadvantage is that if too few beams are used, there will be image noise. However, there are ways such as Importance Sampling that can reduce the noise.
Path tracing and light ray tracing
Although diffuse ray tracing enables numerous effects, it is still not able to simulate global lighting with effects such as diffuse interreflection and caustics ( bright spots of light created by the bundling of light). This is due to the fact that secondary rays are emitted in the case of specular reflections, but not in the case of diffuse surfaces.
In his 1986 publication, James Kajiya described the rendering equation , which forms the mathematical basis for all methods of global lighting. The "brightness" contributed by a beam is interpreted radiometrically correctly as radiance . Kajiya showed that for global illumination, secondary rays have to be emitted from all surfaces. He also pointed out that a render tree has the disadvantage that too much work is wasted on the calculations in a great hierarchy depth and that it is better to send out a single ray at a time. This method is known today as path tracing , since a ray seeks its "path" through the scene from the eye point. Path tracing has a rigorous mathematical and physical basis.
If the secondary beam emitted from a diffuse surface hits a light source directly during path tracing, this brightness component is usually ignored. Instead, the proportion of direct lighting is still calculated using a shadow ray. Alternatively, the direct lighting can be calculated in that only one secondary beam is emitted in accordance with the local lighting model and, if it hits a light source directly, its radiance is returned. Which of these two methods is more efficient depends on the local lighting model of the surface and on the solid angle of the light source viewed from the surface . The conceptually simpler variant of path tracing, in which no shadow rays are emitted, is known as adjoint photon tracing .
Although path tracing can simulate global lighting, the method becomes less efficient with small light sources. In particular, caustics and their reflections are very noisy with path tracing, unless very many rays are emitted. Therefore, other methods or extensions based on path tracing are mostly used.
Light ray tracing is a rare variant in which the light rays are not emitted from the eye point, but from the light sources. The pixels that are hit by the beam on the image plane are colored. This allows certain effects such as caustics to be simulated, but other effects can only be simulated very inefficiently because many rays miss the image plane.
Further developments
Since some effects can only be simulated well from the eye point, others only from the light sources, algorithms were developed that combine both methods. The goal is to be able to efficiently render scenes with light distribution and reflection of any complexity.
- Bidirectional path tracing ,
- Developed independently in 1993 and 1994 by Lafortune / Willems and E. Veach / Leonidas J. Guibas , is a direct extension of path tracing , in which rays are sent from both the eye point and the light sources and both paths are then combined. The points of impact of the light path are used as point-shaped virtual light sources to illuminate the eye path. Bidirectional path tracing can be viewed as a generalization of path tracing, adjoint photon tracing or light ray tracing, as it takes into account the exchange of light between all possible combinations of points of impact of the two paths. The method usually offers better performance than pure path tracing, especially when calculating caustics, but does not completely eliminate its problems.
- Metropolis Light Transport (MLT)
- is an extension of the bidirectional path tracing and was introduced in 1997 by Veach and Guibas. With MLT, the light beams are emitted in such a way that they adapt to the lighting and “explore” the scene. The idea of the procedure is not to discard "good" path combinations, over which a lot of energy is transported, immediately after they have been found, but to continue to use them. MLT often offers significant speed advantages and reasonable results in scenes that are difficult to simulate correctly with other (previous) algorithms. In the same way as path tracing and bidirectional path tracing, MLT delivers statistically accurate images if implemented appropriately , that is, the only deviation from the ideal image is the image noise; other errors are excluded.
- Photon mapping
- was published by Jensen in 1995. The process consists in emitting particles from the light sources and storing them in a special structure that is independent of the geometry. This algorithm was a breakthrough in that it made it possible to save the lighting in a preprocessing step and to reconstruct it relatively quickly during the rendering process.
- Photon mapping is not a stand-alone rendering process, but serves to complement other ray tracing methods - mostly to extend diffuse ray tracing to global lighting. However, photon mapping is not true to expectations, its precision is difficult to control intuitively and less robust than MLT. This is particularly noticeable in scenes with difficult lighting conditions.
Overview
| Ray tracing process | shadow | Light reflection / refraction / scattering | lighting | Example image |
|---|---|---|---|---|
| Only occlusion calculation | No | No | No |

|
|
Simulation of shadows (with only one shadow ray) |
Hard shadows only | No | Direct lighting only |

|
| Recursive ray tracing | Hard shadows only | Only with reflective / refractive surfaces | Direct lighting or reflection / refraction only |

|
| Diffuse ray tracing | Completely | Only with reflective / refractive surfaces | Direct lighting or reflection / refraction only |

|
|
Path tracing (and subsequent procedures) |
Completely | Complete (also diffuse ) | Complete ( global lighting ) |

|
Special
The listed common variants of ray tracing can be expanded to enable additional effects. Some examples:
- Constructive Solid Geometry (CSG)
- is a common modeling method in which objects are assembled from other objects. Ray tracing can be expanded to include CSG functionality relatively easily.
- Texture mapping
- as well as displacement mapping and bump mapping are also possible for ray tracing. With the latter method, however, it must be ensured that the generated reflection directions always point away from the object.
- Volume scatter
- enables the realistic simulation of partially translucent objects and objects that scatter light. This includes, for example, milk or leaves , but also the blue of the sky and atmospheric conditions.
- Spectral rendering
- Most common ray tracers use the RGB color space to represent colors, which is only an approximation of the continuous light spectrum and is not always physically plausible. By using a representation for the color that is dependent on the wavelength of the light, effects such as metamerism and dispersion can be simulated. Also polarization and fluorescence are possible.
- High dynamic range rendering
- By calculating the color values during ray tracing using floating point numbers and storing them in HDR images with a high contrast range, it is possible to subsequently change the brightness and contrast of rendered images without any loss of quality. With image-based lighting , the scene to be rendered is enclosed in an HDR image, which enables realistic lighting through recorded surroundings.
- Relativistic ray tracing
- By considering the formulas for the special theory of relativity , the optical effects that occur with curved space-time can be illustrated. The beam paths are modified, taking into account the high speeds and masses; there are also changes in brightness and color.
Areas of application
Computer graphics
Ray tracing calculations are considered to be very time consuming. Ray tracing is therefore primarily used in the generation of representations in which the quality is more important than the calculation time. Computing an image with ray tracing can take any length of time - in practice often several hours, in individual cases even several days - depending on the technology used, the complexity of the scene, the hardware used and the desired quality. In areas such as virtual reality , in which spatial representations have to be calculated in real time , ray tracing has not been able to establish itself so far. Computer animation films are predominantly produced with the REYES system, in which ray tracing calculations are avoided as far as possible. Ray tracing was occasionally used by the demo scene .
However, compared to common real -time renderers based on Z-Buffer , ray tracing has several advantages: a simple implementation with manageable complexity , a high degree of flexibility in contrast to the graphics pipeline and the easier interchangeability of the shaders and thus easier implementation of new shaders. The speed of ray tracing must therefore be related to the image quality achieved. There is no alternative to ray tracing for the demanding quality requirements of realistic image synthesis, especially for complicated scenes with any material.
Efforts are being made to implement real-time ray tracers for complex scenes, which has already been achieved under certain conditions with processor and memory -optimized software solutions. Implementations of ray tracing optimized for hardware show that the future widespread use of ray tracing in real time is conceivable. With these applications, projects, like those OpenRT - programming and various implementations for programmable GPUs ( GPGPU ). In addition, special architectures for hardware-accelerated ray tracing were developed.
Further areas of application
The ray tracing principle can be extended to any application areas in which the propagation of waves in a scene is to be simulated. Rays always represent the normal vectors to a wave front . In auralization and high-frequency technology one tries to simulate the effects of a scene on the acoustics or on an electromagnetic field . The aim is to calculate the proportion of energy that is transmitted from a transmitter to a receiver over the various possible paths through the scene for certain frequencies.
In acoustics, ray tracing is one way of solving this problem, in addition to the mirror sound source method and diffuse sound calculation. For the simulation, the material properties of the various bodies and the attenuation of the sound by the air must be taken into account.
One way of finding the transmission paths is to send rays from a source isotropically (in all directions), possibly reflecting them off the objects with a loss of energy, and to determine the total energy of the rays hitting the receiver. This method is called ray launching . Rays can also have a certain “shape” - for example that of a tube - in order to be able to simulate point-shaped receivers. The disadvantage of this method is its slowness, since many beams never reach the receiver and a large number is necessary for precise statistics.
Another problem arises from the fact that the wavelength is often not negligible compared to the dimensions of the bodies within a scene. If the diffraction of rays is not taken into account, noticeable errors can occur in the simulation.
literature
- Philip Dutré, Philippe Bekaert, Kavita Bala: Advanced Global Illumination. AK Peters, Natick MA 2003, ISBN 1-56881-177-2 ( advancedglobalillumination.com )
- Andrew S. Glassner: An Introduction to Ray tracing. Morgan Kaufmann, London 1989, ISBN 0-12-286160-4
- Andrew S. Glassner: Principles of Digital Image Synthesis. Morgan Kaufmann, London 1995, ISBN 1-55860-276-3
- Matt Pharr, Greg Humphreys: Physically Based Rendering. From theory to implementation. Morgan Kaufmann, London 2004, ISBN 0-12-553180-X ( pbrt.org )
- Peter Shirley: Realistic Ray Tracing. AK Peters, Natick MA 2003, ISBN 1-56881-198-5
- Kevin G. Suffern: Ray Tracing from the Ground Up. AK Peters, Wellesley MA 2007, ISBN 978-1-56881-272-4
Web links
- Ray Tracing News (English)
- List of intersection test algorithms for various primitive types (English)
- Tom's Hardware: "When Will Ray Tracing Replace Rasterization?" (English)
- Illusion forge: "Instructional video ray tracing"
Remarks
- ↑ Hans-Joachim Bungartz u. a .: Introduction to computer graphics: Fundamentals, geometric modeling, algorithms, p. 135. Vieweg, Braunschweig 2002, ISBN 3-528-16769-6
- ↑ Beat Brüderlin, Andreas Meier: Computer graphics and geometric modeling, p. 154. Teubner, Stuttgart 2001, ISBN 3-519-02948-0
- ↑ Terrence Masson: CG 101: A Computer Graphics Industry Reference. P. 267. Digital Fauxtography 2007, ISBN 0-9778710-0-2
- ↑ Arthur Appel: Some Techniques for Shading Machine Renderings of Solids. In Proceedings of the Spring Joint Computer Conference 1968. pp. 37-45. AFIPS Press, Arlington
- ^ Mathematical Applications Group, Inc .: 3-D Simulated Graphics Offered by Service Bureau. Datamation 13, 1 (Feb. 1968): 69, ISSN 0011-6963
- ^ Robert Goldstein, Roger Nagel: 3-D Visual Simulation. Simulation 16, 1 (Jan. 1971): 25-31, ISSN 0037-5497
- ↑ Terrence Masson: CG 101: A Computer Graphics Industry Reference. In: Digital Fauxtography , 2007, ISBN 0-9778710-0-2 , p. 162.
- ↑ Oliver Abert et al. a .: Direct and Fast Ray Tracing of NURBS Surfaces. In Proceedings of IEEE Symposium on Interactive Ray Tracing 2006. pp. 161-168. IEEE, Salt Lake City 2006, ISBN 1-4244-0693-5 ( PDF, 700 kB ( Memento of the original dated December 2, 2007 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and Archive link according to instructions and then remove this note. )
- ↑ Vlastimil Havran et al. a .: Statistical Comparison of Ray-Shooting Efficiency Schemes. Technical Report TR-186-2-00-14, Institute of Computer Graphics and Algorithms, Vienna University of Technology 2000 ( ist.psu.edu )
- ↑ Ingo Wald, Vlastimil Havran: On building fast kd-trees for ray tracing, and on doing that in O (N log N). In Proceedings of IEEE Symposium on Interactive Ray Tracing 2006. pp. 61-69. IEEE, Salt Lake City 2006, ISBN 1-4244-0693-5 ( PDF, 230 kB )
- ↑ Ingo Wald u. a .: Interactive Rendering with Coherent Ray Tracing. Computer Graphics Forum 20, 3 (Sep. 2001), pp. 153-164, ISSN 0167-7055 ( graphics.cs.uni-sb.de ( Memento of the original from June 5, 2005 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. )
- ↑ Alexander Reshetov et al. a .: Multi-Level Ray Tracing Algorithm. ACM Transactions on Graphics 24, 3 (July 2005): 1176–1185, ISSN 0730-0301 ( PDF; 400 kB )
- ^ Douglas Scott Kay: Transparency, Refraction and Ray Tracing for Computer Synthesized Images. Thesis, Cornell University, Ithaca 1979
- ^ Turner Whitted: An Improved Illumination Model for Shaded Display. Communications of the ACM 23, 6 (June 1980): 343-349, ISSN 0001-0782 ( PDF, 4.6 MB )
- ↑ Robert Cook et al. a .: Distributed ray tracing. ACM SIGGRAPH Computer Graphics 18, 3 (July 1984), pp. 137-145, ISSN 0097-8930
- ↑ Peter Shirley, Changyaw Wang, Kurt Zimmermann: Monte Carlo Techniques for Direct Lighting Calculations. ACM Transactions on Graphics 15, 1 (Jan. 1996), pp. 1–36 ( PDF; 400 kB )
- ↑ James Kajiya: The Rendering Equation. ACM SIGGRAPH Computer Graphics 20, 4 (Aug. 1986), pp. 143-150, ISSN 0097-8930
- ↑ Eric Veach, Leonidas J. Guibas: Optimally combining sampling techniques for Monte Carlo rendering. In SIGGRAPH '95 Proceedings, pp. 419-428. ACM, New York 1995, ISBN 0-89791-701-4 ( graphics.stanford.edu )
- ^ R. Keith Morley et al. a .: Image synthesis using adjoint photons. In Proceedings of Graphics Interface 2006, pp. 179-186. Canadian Information Processing Society, Toronto 2006, ISBN 1-56881-308-2 ( PDF, 4.7 MB )
- ↑ Eric Lafortune, Yves Willems: Bi-Directional Path Tracing. In Proceedings of Compugraphics '93. Pp. 145-153. Alvor 1993 ( graphics.cornell.edu )
- ↑ Eric Veach, Leonidas Guibas: Bidirectional Estimators for Light Transport. In Eurographics Rendering Workshop 1994 Proceedings. Pp. 147-162. Darmstadt 1994 ( graphics.stanford.edu )
- ^ E. Veach, LJ Guibas: Metropolis Light Transport. In SIGGRAPH '97 Proceedings. Pp. 65-76. ACM Press, New York 1997, ISBN 0-89791-896-7 ( graphics.stanford.edu )
- ^ Henrik Wann Jensen and Niels Jørgen Christensen: Photon Maps in Bidirectional Monte Carlo Ray Tracing of Complex Objects. Computers and Graphics 19, 2 (Mar. 1995): 215-224, ISSN 0097-8493 ( graphics.stanford.edu )
- ^ Peter Atherton: A Scan-line Hidden Surface Removal Procedure for Constructive Solid Geometry. ACM SIGGRAPH Computer Graphics 17, 3 (July 1983), pp. 73-82, ISSN 0097-8930
- ↑ Alexander Wilkie u. a .: Combined Rendering of Polarization and Fluorescence Effects. In Proceedings of the 12th Eurographics Workshop on Rendering Techniques . Springer, London 2001, ISBN 3-211-83709-4 , pp. 197–204 ( PDF, 2.9 MB )
- ↑ Daniel Weiskopf u. a .: Real-World Relativity: Image-Based Special Relativistic Visualization. In IEEE Visualization: Proceedings of the Conference on Visualization 2000. pp. 303-310. IEEE Computer Society Press, Salt Lake City 2000, ISBN 1-58113-309-X ( PDF, 640 kB ( Memento of the original from June 13, 2007 in the Internet Archive ) Info: The archive link has been inserted automatically and has not yet been checked. Please check Original and archive link according to instructions and then remove this note. )
- ↑ Jörg Schmittler u. a .: SaarCOR - A Hardware Architecture for Ray Tracing. In Proceedings of the SIGGRAPH / EUROGRAPHICS Conference On Graphics Hardware. Pp. 27-36. Eurographics, Aire-la-Ville 2002, ISBN 1-58113-580-7 ( PDF, 1.0 MB ( Memento of the original from July 28, 2007 in the Internet Archive ) Info: The archive link has been inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this note. )







