Antialiasing (computer graphics)
Anti-aliasing ( AA , also anti-aliasing or anti-aliasing ) is the reduction of adverse effects caused by the limited pixel grid (see image resolution and aliasing ) or by the aliasing in the generation of a computer graphics created (computer generated 2D or 3D graphics) can.
With antialiasing, the image content is usually not only evaluated ( scanned ) at the pixel but also at other positions and included in the calculation of the pixel color. In addition, some techniques developed for real-time rendering reduce the staircase effect through subsequent filtering or tracing of the image.
Antialiasing methods differ in the scheme used to distribute the sampling points and in the choice of the reconstruction filter, which determines how the color values determined at the sampling points are weighted.
background
Sampling and prealiasing
The creation of a raster graphic from an image description by means of rasterization or image synthesis ultimately consists in assigning a color to each discrete pixel. In the context of signal processing theory, this process can be interpreted as sampling a signal. Computer graphics are unique in that many signals are available here as abstract image descriptions that can only be algorithmically evaluated at individual points . One example are images that are calculated using ray tracing . Such signals can also be referred to as procedural signals .
When rastering without antialiasing, the image description is only evaluated on the pixels; other points of the image do not flow into the color of the pixels. One problem with this method is that small figures are not captured by the pixel grid and therefore do not appear in the rasterized image. If small image details are arranged regularly, they interfere with the pixel grid, which leads to aliasing effects. This is illustrated by the computer-generated image of an infinitely large chessboard.
The period length of the signal is here equal to the size of two projected checkerboard fields. As soon as the period length falls below two pixel intervals , i.e. the Nyquist frequency is exceeded, the signal is undersampled . Certain checkerboard fields are no longer captured by the pixel grid; the checkerboard pattern is destroyed. According to the Nyquist-Shannon sampling theorem , aliasing effects occur, in which a high original frequency is expressed in the sampling as a misleading low frequency: Near the horizon, the false impression arises that the original signal contains strangely large fields. The illustrative term “picket fence effect”, which is occasionally used in German, makes this clear: The spatial frequency spectrum of the original image is viewed through a device used by the playback device, e.g. B. the screen, fixed frequency resolution - the picket fence. This type of aliasing that is a result of the sampling method is called prealiasing .
Even if the image were calculated with higher image resolutions and thus higher sampling rates, disruptive aliasing effects would appear near the horizon, but only from a higher frequency. This is due to the fact that in the chessboard scene the fields become smaller and smaller towards the horizon and thus the spatial frequency is unlimited.
Reconstruction and Postaliasing
In signal processing, reconstruction refers to the conversion of a discrete signal into a continuous signal by interpolating between the individual samples using a reconstruction filter. In computer graphics, the term is interpreted a little differently, as no continuous signal is generated here. Rather, reconstruction in this context means calculating the color of a pixel from the color values in the vicinity of the pixel, for example in order to scale a raster graphic . The reconstruction filter used here is a two-dimensional function that is centered over the pixel to be calculated and indicates how sample values are weighted. In the case of a conical filter, a color value determined directly at the pixel is given the highest weighting, while values further away have less influence. Color values lying outside the carrier of the reconstruction filter are ignored. The color value of the pixel is the sum of the weighted color values. This operation corresponds to a convolution with a low-pass filter of one order of the selected anti-aliasing level.
Antialiasing using a box filter, which calculates the mean value of all color values within a square around the pixel, is also known as " Unweighted Area Sampling ". In other cases one speaks of “weighted area sampling”. Examples of reconstruction filters with weighted area scanning are the Mitchell-Netravali filters (bicubic filters), the Lanczos filters or the Gaussian filters .
- Antialiasing with various reconstruction filters
A sampled, discrete signal is a series of frequency-shifted copies of the useful signal in the frequency domain . The reconstruction can be interpreted as isolating the original useful signal, excluding the copies. If the reconstruction filter not only isolates the useful signal, but also includes parts of its copies (see diagram on the right), postaliasing occurs. Postaliasing thus arises from the selection of an unsuitable reconstruction filter and can even occur if the original signal was sampled with a sufficient sampling rate and without prealiasing.

Staircase effect
The term staircase effect describes the angular, “stair-like” appearance of grid-like figures. In the literature it has often been claimed that the staircase effect is a consequence of the aliasing effect. However, this is wrong, as can be shown by comparing the Fourier transforms of the ideal and the rasterized image. The staircase effect does not manifest itself in that a high frequency appears as a disturbing low frequency, but is a direct consequence of the limited resolution of the output device. The staircase effect is particularly noticeable in animations, as figures seem to move jerkily and very thin or small objects seem to flicker when moving.
Procedure
Without the use of antialiasing, each pixel is scanned only once at a position that is constant relative to the pixel. With antialiasing, the image description is evaluated at several positions and / or at different positions relative to the pixel. The color of the pixel is calculated from the values determined in this way in accordance with a reconstruction filter. By choosing a suitable scanning method, prealiasing can be reduced or avoided by choosing suitable reconstruction filters. The term "anti-aliasing" is misleading insofar as anti-aliasing is used not only against aliasing effects, but also against the staircase effect and other undesirable effects, such as small figures falling through the pixel grid. In 1977, Franklin Crow provided the first description of the aliasing effect as a cause of image artifacts in computer graphics.
The traditional anti-aliasing techniques used in signal processing cannot easily be transferred to computer graphics. This is because, from the point of view of signal processing, computer graphics, in contrast to audio signals, for example, have the following peculiarities:
- The signals occurring in computer graphics are artificial, abstract descriptions of images, which are often not recorded in their entirety, but can only be evaluated at individual points.
- Computer graphics usually contain hard object edges, which corresponds in places to infinite spatial frequencies. A perfect reconstruction of the output signal using an ideal low-pass filter (sinc filter) is therefore not possible.
- Image descriptions are often not scanned regularly, but at irregularly distributed positions.
- Human visual perception is particularly sensitive to the artifacts caused by poor anti-aliasing methods.
Practical considerations
For antialiasing to work best, it is essential to apply gamma correction . Lines and polygon edges that have been rasterized with antialiasing but without gamma correction tend to have a “rope-like” appearance. Antialiasing can also be combined with sub-pixel rendering in order to benefit from the horizontal division of a screen pixel into adjacent primary colors. In the area of pixel art , anti-aliasing does not happen automatically, but is achieved by the graphic artist directly by setting individual pixels.
Antialiasing requires additional computing power, which is not negligible, especially with real-time rendering. Another disadvantage is that an anti-aliased image can be perceived as blurred; like other defects, the blurring depends on the reconstruction filter used. Conversely, the mere subsequent blurring of a rastered image does not represent conventional antialiasing, since the original image description is not evaluated here; however, some real-time technologies are based on such a procedure (see section Hardware Implementation ). Images that already have prealiasing effects, such as print rasters scanned with low resolution , can in part be corrected in the frequency range afterwards by removing the disruptive Fourier components . Techniques also exist to remove stair treads from images that were created without anti-aliasing.
Prefiltering and area scanning
In computer graphics, prefiltering is the process of determining the color of a pixel without taking individual samples. Rather, the color is calculated directly from the image description. As described above, the color value of a pixel corresponds to the sum weighted by the reconstruction filter of all color values of the objects which are overlapped by the carrier of the filter. Prefiltering is only possible for image descriptions whose convolution can be calculated analytically with the reconstruction filter, i.e. can be expressed in the form of known functions. This includes simple geometric objects such as lines. On the other hand, prefiltering cannot be applied to procedural signals, since these can only be sampled at individual points.
One of the first prefiltering methods for computer graphics was described by Edwin Catmull in 1978 . Its algorithm uses weighted area sampling. The color of a pixel is calculated by clipping the polygons that make up the image against the pixel and thus determining their area share. This process was so slow that it could only be used with two-dimensional computer animation with a few large polygons. Later methods attempted to approximate the area proportions of the object fragments by means of bit masks - including Carpenter's A-Buffer , sometimes called multisampling - or to use lookup tables . In addition, anti-aliasing processes tailored to the rasterization of basic shapes such as lines and circles have been developed, see rasterization of lines and rasterization of circles . High-quality pre-filtering anti-aliasing of any curves with various reconstruction filters is also possible.
Post filtering and point sampling
Post filtering or supersampling is mainly used when the image description can only be evaluated at individual points. For this purpose, several sample values are used to calculate the color of each pixel, which are weighted by means of a reconstruction filter. From a mathematical point of view, postfiltering is a method for numerically approximating the convolution integral .
Multisampling methods differ in the number and distribution of the sampling positions per pixel. Real-time rendering tends to use the same pattern for all pixels. Some patterns define different weightings for the samples, which is why they can also be viewed as linear reconstruction filters. If the carrier of a reconstruction filter extends over several pixels and several pixels share some sample values, this is called sample sharing.
The following ordered patterns are common:

|
Orderly. The scanning positions are tiled along the axes. |

|
Chess board. The scanning positions are distributed like a checkerboard pattern. |

|
RGSS. This pattern, called Rotated Grid SuperSampling, gives better results than the ordered pattern for nearly horizontal or vertical edges where antialiasing is most needed. |

|
Quincunx . In thispattern developedby Nvidia , also known as High Resolution Antialiasing (HRAA), four pixels each share the sample values in the corners, each of which is only weighted to a quarter of the sample value in the middle. Together with the position in the middle, only two scans per pixel are required on average. |

|
Flipquad. Four samples are divided by two pixels each; the pattern is mirror-inverted for neighboring pixels. This gives an average of two samples per pixel. |
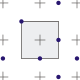
|
Fliptri. Three samples are used for each pixel. One of the values is divided by four pixels, the other two by two pixels. On average, only 1.25 samples per pixel are necessary. Different weightings can be used for this pattern. Combinations of the flipquad and fliptri patterns are also possible. |
In contrast to the ordered patterns, in the case of stochastic scanning the scanning pattern varies relative to the pixel. This replaces aliasing with noise, which is perceived as less irritating. At the same time, however, it is desirable to keep the sampling points far apart from one another in order to ensure that the sampling is as representative as possible. Stochastic scanning patterns are mainly used in realistic image synthesis.

|
Random distribution. The sampling positions are determined by a pseudo random number generator . This leads to an undesirable local accumulation of positions. |

|
Jittering. The area around a pixel is regularly divided into squares, in each of which a sampling position is randomly distributed. The accumulation of sample positions is thereby reduced; however, only exactly sampling points per pixel can be used. |

|
N -Rooks. In this scheme, also known as Latin Hypercube Sampling , there is only one sampling point in each column and row of a grid. To do this, a scanning position is first placed randomly in each cell along the grid diagonal, then the lines of the grid are randomly swapped : |

|
Low-discrepancy distribution. Low -discrepancy sequences such as the Halton sequence are used to generate the scanning positions , which generate elements that are far apart. |

|
Poisson Disk. In Poisson disk scanning , the scanning positions are randomly distributed, ensuring that they are at a minimum distance from one another. Numerous methods of varying quality and efficiency have been developed for generating Poisson disk distributions. |
Another method is adaptive supersampling. The number of sampling points is varied over the image. The decision as to whether further scans should be carried out is made on the basis of local criteria such as contrast. However, such techniques are usually not true to expectations and can lead to artifacts.
Instead of distributing the sampling points more or less evenly and weighting the values determined there using a reconstruction filter, importance sampling can be used to calculate the pixel color . The sample values are distributed according to the shape of the reconstruction filter (more sample points close to the pixel) and weighted equally. This method leads to a less noisy result.
Hardware implementation
Antialiasing can be implemented directly in hardware for real-time rendering using graphics cards. Initially only very high quality and expensive graphics cards supported this technology in graphics interfaces such as OpenGL . With the advent of affordable, high-performance desktop graphics chips like the 3dfx VSA-100 or NV10 from Nvidia , real-time anti-aliasing became available to ordinary users as well.
The conceptually simplest method is full-scene antialiasing (FSAA). The images are rendered with a higher resolution and then downscaled. Another method uses the accumulation buffer . To render an image with four sampling points per pixel, four images are written to the buffer one after the other, each offset by a fraction of a pixel pitch in all directions. A variant of the accumulation buffer is the T-buffer . It consists of two, four, or more image and Z buffers , each of which can be used for rendering. A mask determines where a triangle is sent; in the end all buffers are combined. If a screen offset is set individually for each buffer, antialiasing can be achieved by sending each triangle to all buffers in parallel. The advantage of the accumulation buffer and the T-buffer is that not only ordered scanning positions are possible. So-called multisampling is also often used, which differs from supersampling in that shader calculations are not carried out for every sampling position .
The A-buffer can also be implemented in hardware as a prefiltering algorithm. Other hardware-based prefiltering algorithms have been published, including the Z³ method, which was introduced in a similar form by Matrox under the name Fragment Antialiasing (FAA). The advantage of prefiltering is that only the areas with polygon edges are actually antialiased.
In practice, real-time antialiasing often uses only a few samples per pixel and the box filter or simple linear reconstruction filters. At least one graphics card, the Wildcat from 3DLabs , uses a stochastic sampling method with jittering. The professional SAGE graphics system from Sun Microsystems allows a programmable scanning pattern with a weighted reconstruction filter that extends over 128 × 128 pixels.
Another method supported by DirectX is edge antialiasing. After the scene has been rendered, the object edges are traced with smoothed lines in a second pass. With deferred shading , a technique used in some newer computer games, the geometry of the objects is calculated independently of their lighting. Since no conventional hardware anti-aliasing can be used here, the staircase effect can be concealed by edge detection and blurring of the object edges. A similar method is Morphological Antialiasing (MLAA). The pixel pattern on the edges determines the type of soft focus.
The perspective of textures in real-time rendering is sometimes referred to as "texture antialiasing." The techniques used for this, such as mip mapping and anisotropic filtering , do not, however, carry out antialiasing in the usual sense, since no new images are generated from a mathematical image description. Rather, with texture mapping, existing raster graphics are scaled in perspective, except for procedural textures that are calculated during the rendering process.
literature
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. AK Peters, Natick Mass 2002, ISBN 1-56881-182-9 , pp. 84-101.
- James Foley et al: Computer Graphics: Principles and Practice. Addison-Wesley, Reading 1995, ISBN 0-201-84840-6 , especially pp. 617-647.
- Matt Pharr, Greg Humphreys: Physically Based Rendering. From theory to implementation. Morgan Kaufmann, London 2004, ISBN 0-12-553180-X , pp. 279-367 ( PDF; 7 MB ).
- Alan Watt: 3D Computer Graphics. Addison-Wesley, Harlow 2000, ISBN 0-201-39855-9 , pp. 392-417.
Web links
Individual evidence
- ^ A b c Don Mitchell, Arun Netravali : Reconstruction Filters in Computer Graphics. ACM SIGGRAPH Computer Graphics 22, 4 (Aug. 1988): 221-228, ISSN 0097-8930
- ↑ Beate Meffert , Olaf Hochmuth: Signal processing tools: Fundamentals, application examples, exercises. Pearson Studium, Munich 2004, ISBN 3-8273-7065-5 , p. 180 ff.
- ^ Alan Watt: 3D Computer Graphics. P. 399.
- ↑ James Foley et al: Computer Graphics: Principles and Practice. Pp. 132-137.
- ^ Alan Watt: 3D Computer Graphics. P. 397.
- ^ Franklin Crow: The Aliasing Problem in Computer-Generated Shaded Images. Communications of the ACM 20:11 (November 1977): 799-805, ISSN 0001-0782
- ^ AR Forrest: Antialiasing In Practice. In: RA Earnshaw (Ed.): Fundamental Algorithms for Computer Graphics (= NATO ASI Series F.17). Springer, Berlin 1985, ISBN 3-540-13920-6 , pp. 113-134.
- ↑ Lei Yang et al.: Antialiasing recovery. ACM Transactions on Graphics 30, 3 (May 2011): 22: 1–22: 9, ISSN 0730-0301 ( online )
- ^ Edwin Catmull: A Hidden-Surface Algorithm with Anti-Aliasing. ACM SIGGRAPH Computer Graphics 12, 3 (Aug 1978): 6-11
- ^ Alan Watt: 3D Computer Graphics. P. 403.
- ^ Loren Carpenter: The A-Buffer, an Antialiased Hidden Surface Method. In: SIGGRAPH '84 Proceedings. ACM, New York 1984, ISBN 0-89791-138-5 , pp. 103-108.
- ^ Eugene Fiume et al.: A Parallel Scan Conversion Algorithm with Anti-Aliasing for a General-Purpose Ultracomputer. In: SIGGRAPH '83 Proceedings. ACM, New York 1983, ISBN 0-89791-109-1 , pp. 141-150.
- ↑ Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. P. 94.
- ^ Greg Abram, Lee Westover: Efficient Alias-Free Rendering Using Bit-Masks and Look-Up Tables. ACM SIGGRAPH Computer Graphics 19,3 (July 1985): 53-59
- ^ AE Fabris, AR Forrest: Antialiasing of Curves by Discrete Pre-filtering. In: SIGGRAPH '97 Proceedings. ACM Press, New York 1997, ISBN 0-89791-896-7 , pp. 317-326 ( online ).
- ↑ a b Samuli Laine, Timo Aila: A Weighted Error Metric and Optimization Method for Antialiasing Patterns. Computer Graphics Forum 25, 1 (Mar. 2006): 83–94, ISSN 1467-8659 ( PDF; 420 kB ( Memento from May 8, 2006 in the Internet Archive ))
- ↑ NVIDIA Corporation: HRAA: High-resolution Antialiasing through Multisampling. Technical Brief, 2001 ( PDF; 2.5 MB ).
- ↑ Tomas Akenine-Möller, Jacob Ström: Graphics for the Masses: A Hardware Rasterization Architecture for Mobile Phones. ACM Transactions on Graphics 22, 3 (Jul. 2003): 801-808
- ↑ Tomas Akenine-Moller: An Extremely Inexpensive Multisampling Scheme. Technical report, Chalmers University of Technology / Ericsson Mobile Platforms AB, Aug. 2003, p. 79 ( PDF; 165 kB ).
- ↑ Jon Hasselgren et al: A Family of Inexpensive Sampling Schemes. Computer Graphics Forum 24, 4 (Dec. 2005): 843-848
- ↑ Ares Lagae, Philip Dutré: A Comparison of Methods for Generating Poisson disc distribution. Report CW 459, Department of Computer Science, Katholieke Universiteit Leuven 2006 A Comparison of Methods for Generating Poisson Disk Distributions. Retrieved July 13, 2019 .
- ^ Turner Whitted: An Improved Illumination Model for Shaded Display. Communications of the ACM 23, 6 (June 1980): 343–349 ( PDF; 4.6 MB )
- ↑ David Kirk, James Arvo: Unbiased Sampling Techniques for Image Synthesis. ACM SIGGRAPH Computer Graphics 25, 4 (July 1991): 153-156
- ↑ Manfred Ernst, Marc Stamminger, Gunther Greiner: filter importance sampling. In: Proceedings of IEEE Symposium on Interactive Ray Tracing, 2006. ISBN 1-4244-0693-5 , pp 125-132 ( . Filter importance sampling Retrieved on July 13, 2019 . ).
- ↑ Stephanie Winner et al: Hardware Accelerated Rendering Of Antialiasing Using A Modified A-buffer Algorithm. In: SIGGRAPH '97 Proceedings. ACM Press, New York 1997, ISBN 0-89791-896-7 , pp. 307-316.
- ↑ Norman Jouppi, Chun-Fa Chang: Z³: An Economical Hardware Technique for High-Quality Anti-Aliasing and Transparency. In: Proceedings of the Eurographics / SIGGRAPH Workshop on Graphics Hardware '99. ACM, New York 1999, ISBN 1-58113-170-4 , pp. 85-93.
- ^ Michael Deering, David Naegle: The SAGE Graphics Architecture. In SIGGRAPH '02 Proceedings. ACM, New York 2002, ISBN 1-58113-521-1 , pp. 683-692 ( PDF; 190 kB ).
- ↑ http://msdn.microsoft.com/archive/default.asp?url=/archive/en-us/dx8_vb/directx_vb/graphics_using_3b8z.asp (link not available)
- ^ Fabio Policarpo, Francisco Fonseca: Deferred Shading Tutorial. ( PDF; 1.5 MB ( memento of March 6, 2009 in the Internet Archive ))
- ↑ Alexander Reshetov: Morphological Antialiasing. In: Proceedings of High Performance Graphics. ACM, New York 2009, ISBN 978-1-60558-603-8 , pp. 109–116 ( PDF; 1.8 MB ( memento of August 20, 2010 in the Internet Archive )).













