Reconstruction filter

In the signal processing a is reconstruction filter , a filter that determines, as in the conversion of a discrete individual in a continuous signal samples interpolated to be.

With uniform sampling over the Nyquist frequency , the Sinc function is the theoretically ideal reconstruction filter , since its Fourier transformation is a square wave function ( ideal low pass ) that completely isolates the useful signal in the frequency range. The original signal can thus be completely restored.

In electronics, a reconstruction filter is applied to the output signal of a digital-to-analog converter .

Reconstruction filters in computer graphics

In computer graphics , no distinction is made between reconstruction filters and anti-aliasing filters . Instead of generating a continuous signal, the color of a pixel is calculated from color values ​​determined in the vicinity of the pixel, for example when scaling images or to apply anti-aliasing . The reconstruction filter used is a two-dimensional function or distribution that is centered over the pixel to be calculated. Since the image description to be scanned in computer graphics almost always contains higher frequencies than can be detected by scanning due to object edges, the low-pass filter (sinc filter) is not ideal.

Construction of two-dimensional filters

When comparing different reconstruction filters, the one-dimensional filters can first be considered. There are two ways in which a one-dimensional reconstruction filter can be converted into a two-dimensional one, namely through radial symmetry and through separation .

In the construction by radial symmetry, a two-dimensional reconstruction filter is generated from the surface of revolution of a one-dimensional filter. The filter value depends solely on the distance from the center of the filter. In order to use radially symmetrical reconstruction filters, the Euclidean distance to the sample values must therefore be calculated.

In the construction by separation, a two-dimensional reconstruction filter is generated by shifting the one-dimensional filter over the X or Y axis and forming the product of the two functions generated in this way. The separable filters generated in this way are well suited for sample values ​​arranged in a grid. In this case, the calculation of the filter value can be replaced by a series of interpolations with the corresponding one-dimensional reconstruction filter. Here, in an intermediate step, the value of the one-dimensional filter at the x -coordinate of the filter center point is calculated for each of the sampling points overlapped by the filter. The value at the center of the filter is then calculated from the vertical points created in this way.

Separable filters lead to anisotropic effects: Image artifacts created by separable filters are not isotropically (evenly distributed in all directions), but rather aligned along the filter construction axes (i.e. horizontally and vertically).

Since only a sequence of one-dimensional interpolations has to be carried out with separable filters and no Euclidean distances are calculated, they can be calculated more quickly than radially symmetric filters.

The Gaussian filter is the only radially symmetrical reconstruction filter that is also separable. With all other filters, the separable and the radially symmetrical generation lead to different results.

Known filters

The following table lists reconstruction filters that are often described or used in computer graphics.

Filter function	description	example Pictures
		Chess board	Zone plate
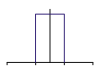
	Box filter. With the box filter, all samples within a square placed around the pixel (usually with an edge length of one pixel distance) have the same weighting. The box filter generally gives poor results because its Fourier transform is a sinc function that does not isolate the desired frequency range well.
	Cone filter. With the cone filter, the weighting decreases with increasing distance from the pixel. It gives slightly better results than the box filter.
	Sinc filter. The Sinc filter is theoretically ideal, but this only applies if the sample is evenly sampled over the Nyquist frequency, which is usually not the case in computer graphics. The sinc filter leads to strong ringing artifacts, especially with edges. In addition, the sinc function has an infinite carrier, so that all samples of the image have to be used to calculate the color value of a pixel. Simply cutting off the sinc function leads to poor results.
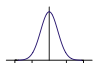
	Gaussian filter. With the Gaussian filter , a Gaussian function is used for the reconstruction . This filter leads to blurring, but aliasing effects are well suppressed.
Parameter selection B = C = ⅓	Mitchell-Netravali filter. The Mitchell-Netravali filters are piece-wise cubic filters with four-pixel wide carriers. They can be changed using two free parameters and were specially designed to investigate the artifacts resulting from reconstruction filters. With a suitable choice of parameters, the filters provide a good compromise between blurring, anisotropy and ringing. The Mitchell-Netravali filters are also known as bicubic filters ; Special cases are cubic B-splines , cardinal splines and Catmull-Rom splines .
Parameter selection a = 3 (filter cut off after three pixels)	Lanczos filter. The Lanczos filter is based on the sinc function, which is typically cut off after two or three pixels and multiplied by a window function to ensure a gradual decrease. It leads to fewer ringing artifacts than the sinc filter.

Uneven scanning

Since image descriptions in computer graphics can have an unlimited frequency spectrum, uneven sampling is generally preferred, so that aliasing effects are replaced by noise. There is no ideal reconstruction method for non-uniform sampling methods, which are also applied to a signal with an unlimited frequency spectrum. The more recent research in signal processing assumes that in such cases a perfect reconstruction is not possible in practice. Instead, an attempt is made to minimize the discrepancy between the original signal and the reconstructed signal, regardless of whether the original signal has an unlimited frequency spectrum or not. However, these theoretical findings have hardly been applied to date.

Artifacts in the reconstruction

In addition to postaliasing, reconstruction filters can lead to a number of other artifacts:

• Sampling frequency ripple occurs when identical samples result in a non-constant reconstructed signal.
• Anisotropic effects arise when the reconstruction filter is not radially symmetrical.
• Ringing ( Gibbs phenomenon ) refers to overshoots or undershoots on hard edges.
• Blur.

literature

• Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation, pp. 279-367. Morgan Kaufmann, London 2004, ISBN 01-2553-180-X ( PDF, 7 MB )
• Ken Turkowski, Steve Gabriel: Filters for Common Resampling Tasks. In Andrew Glassner: Graphics Gems I, pp. 147-165. Academic Press, Boston 1990, ISBN 0-12-286165-5 ( PDF, 160 kB )

Individual evidence

1. ^ Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation, p. 350 f.
2. ^ William Schreiber, Donald Troxel: Transformation Between Continuous and Discrete Representations of Images: A Perceptual Approach. IEEE Transactions on Pattern Analysis and Machine Intelligence 7.2 (Mar 1985): 178-187, ISSN  0018-9340 . Quoted in Don Mitchell, Arun Netravali : Reconstruction Filters in Computer Graphics
3. ↑ Stephen Marschner, Richard Lobb: An Evaluation of Reconstruction Filters for Volume Rendering. In Proceedings of the conference on Visualization '94, pp. 100-107. IEEE Computer Society Press, Los Alamitos 1994, ISBN 0-7803-2521-4 ( online )