Hard-core process

Example of a two-dimensional hard-core point field. The minimum distance between the points is illustrated by the non-overlapping circles; the diameter of the circles corresponds to the minimum distance.

A hard-core process is a stochastic point process in which successive events maintain a specified minimum distance from one another. From the point of view of stochastic geometry , -dimensional point fields, which were generated by hard-core processes, consist of the centers of -dimensional, non-mutually penetrating spheres with a given diameter. ${\ displaystyle n}$ ${\ displaystyle n}$

Depending on the way in which the points are generated, different hard-core processes can be described with different properties. Hard-core processes are mainly used in the theoretical ecology and physics of condensed matter to model various phenomena. Hard-core processes are also used in computer graphics , where they are also referred to as Poisson disk or blue noise scanning .

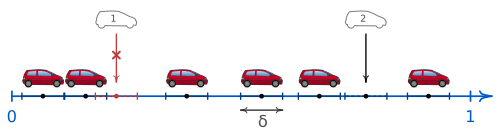
Example: parking problem

A simple example of a hard-core process is the “Random car parking problem”, which was described in 1958 by Alfréd Rényi . Positions on the route (the road) are chosen randomly one after the other. An interval of length (a car) is placed around each of these positions , provided that it does not overlap any of the previously placed intervals. This is a one-dimensional hard-core process, as the centers of the intervals maintain a minimum distance of . ${\ displaystyle [0,1]}$ ${\ displaystyle \ delta}$ ${\ displaystyle \ delta}$

The purely random choice of positions without observing a minimum distance is modeled by the Poisson process . An example of a Poisson process is when raindrops hit the ground. The Poisson process can therefore be viewed as a hard-core process . ${\ displaystyle \ delta = 0}$

Usually only complete hard-core point fields are of practical interest, i.e. point fields in which the hard-core process used for generation has ended and no further point can be added to the given area. Depending on the minimum distance and how closely a process places the points, a complete hard-core point field contains more or fewer points. Rényi was interested in the expected number of intervals that can be placed by random parking.

Various hard-core processes and their simulation

Basic methods

Simple sequential inhibition

The parking problem process described in the previous section can be generalized to two and higher dimensions; He is in the statistics generally considered Simple sequential inhibition (SSI), in physics and chemistry as random sequential adsorption (RSA), in the sequence planning as On-line packing and in computer graphics as dart throwing referred. Here, points are gradually generated by a Poisson process, but only those are taken into account that keep the minimum distance to all previously retained points.

The generation of SSI point fields can be described algorithmically with the following pseudocode . ξ stands for a randomly generated real number between 0 and 1 (or, in the case of multi-dimensional point fields, for tuples of such random numbers).

Punktfeld ← (leer)
Wiederhole n mal
  Kandidat ← ξ
  Für jeden Existierender_Punkt in Punktfeld
    Wenn ||Kandidat - Existierender_Punkt|| < δ
      Nächstes n
  Füge Kandidat zu Punktfeld hinzu

First matérnian process

Bertil Matérn described three types of hard-core processes that result from the thinning of a Poisson process, i. H. by subsequently deleting certain points that were created by a Poisson process. Unlike the SSI process described in the previous section, points are only deleted after the complete Poisson point field has been generated. In the first Matérn process, all points are deleted whose closest neighbor is closer than the minimum distance. If several points are too close together, they will all be deleted.

The algorithm for generating point fields according to the first Matérnian process is as follows:

Punktfeld ← (leer)
Wiederhole n mal
  Punkt ← ξ
  Füge Punkt zu Punktfeld hinzu
 
Zu_löschende_Punkte ← (leer)
Für jeden Punkt in Punktfeld
  Für jeden Nachbarpunkt in Punktfeld
    Wenn ||Punkt - Nachbarpunkt|| < δ
      Wenn Punkt nicht in Zu_löschende_Punkte vorhanden
        Füge Punkt zu Zu_löschende_Punkte hinzu
      Nächster Punkt
 
Für jeden Punkt in Zu_löschende_Punkte
  Lösche Punkt aus Punktfeld

Second matérnian process

In the second Matérn process, the points generated by the Poisson process are provided with an ascending “mark”. Then all points are retained that have no previously generated neighboring points (with a lower marking) within the minimum distance.

The algorithm for the second Matérnian process is as follows:

Punktfeld ← (leer)
Für jedes k von 1 bis n
  Punkt ← ξ
  Punkt.Markierung ← k
  Füge Punkt zu Punktfeld hinzu
 
Zu_löschende_Punkte ← (leer)
Für jeden Punkt in Punktfeld
  Für jeden Nachbarpunkt in Punktfeld
    Wenn ||Punkt - Nachbarpunkt|| < δ und Nachbarpunkt.Markierung < Punkt.Markierung
      Wenn Punkt nicht in Zu_löschende_Punkte vorhanden
        Füge Punkt zu Zu_löschende_Punkte hinzu
      Nächster Punkt
 
Für jeden Punkt in Zu_löschende_Punkte
  Lösche Punkt aus Punktfeld

Third matérnian process

Matérn briefly mentioned a third process that begins like the second. The same process is then repeated with the points of the Poisson process that are not neighboring points of the previously selected points until no more new points can be selected. The algorithm is as follows:

Punktfeld ← (leer)
Kandidaten ← (leer)
Für jedes k von 1 bis n
  Punkt ← ξ
  Punkt.Markierung ← k
  Füge Punkt zu Kandidaten hinzu
 
NeuePunkte ← Wahr
Wiederhole solange NeuePunkte
  NeuePunkte ← Falsch
  Für jeden Punkt in Kandidaten
    Für jeden Nachbarpunkt in Kandidaten
      Wenn ||Punkt - Nachbarpunkt|| < δ und Nachbarpunkt.Markierung < Punkt.Markierung
        Nächster Punkt
    Füge Punkt zu Punktfeld hinzu
    NeuePunkte ← Wahr
 
  Zu_löschende_Punkte ← (leer)
  Für jeden Kandidat in Kandidaten
    Für jeden Punkt in Punktfeld
      Wenn ||Punkt - Kandidat|| < δ
        Wenn Punkt nicht in Zu_löschende_Punkte vorhanden
          Füge Punkt zu Zu_löschende_Punkte hinzu
        Nächster Punkt
 
  Für jeden Punkt in Zu_löschende_Punkte
    Lösche Punkt aus Kandidaten

A more efficient algorithm for simulating Matérn III point fields has been described.

Dead leaves model

Another hard-core process is the dead leaves model (“model of the dead leaves”), also called the non-overlapping germ-grain model (“model of the non-overlapping seeds”). In this process, circles with diameter δ are placed randomly in the plane, whereby they can cover existing circles. The hard-core point field consists of the centers of the uncovered circles (the upper layer) after an infinite number of circles have been added. The process can be simulated in a finite amount of time by placing new circles not above, but below the existing circles, and the process is terminated as soon as the entire area is covered. The process can be transferred to other dimensions.

Simulation of spherical packings

In solid-state physics , special hard-core processes have been developed to simulate and investigate dense random packing of spheres . Usually, horizontally periodic boundary conditions are selected to simulate these point processes.

Sedimentation algorithm

Jodrey and Tory's sedimentation algorithm simulates the packing of spheres by successively dropping spheres into a container. The starting point is an initial spherical layer (“start combination”) on the bottom of the container. Balls are then gradually added, which fall down due to gravity and then, without bouncing off, roll along the existing balls until they come to a stable position. A position is considered stable when the ball touches at least three neighbors (or the floor and two neighbors). If no stable position can be found for a ball after a specified time, the attempt is repeated with a new ball. The process repeats itself until the container is filled.

The density that can be achieved with the sedimentation algorithm is lower than with natural spherical packing; the maximum packing density of the algorithm is approximately 0.58. This is because the optimal position for the balls is not determined, but the first is accepted. There is also an irregularity in the density distribution along the vertical axis. Because of these undesirable properties, the sedimentation algorithm is usually no longer used to simulate close packing of spheres.

Collective rearrangement algorithms

In the group of collective rearrangement algorithms, the specified number of balls remains constant. In the course of the simulation, many of the balls are moved. A well-known algorithm from this group is the force-biased algorithm, which is based on an idea by Jodrey and Torey. A set of randomly distributed, possibly overlapping balls in the container is chosen as a starting point. Only this initial configuration is random, the rest of the algorithm works deterministically. The spheres are shifted away from each other as if a repulsive force field were acting between them. At the same time, the radius of the balls is multiplied by a factor less than 1. This process is repeated until the balls no longer overlap.

Another example of a collective rearrangement algorithm is the Stillinger-Lubachevsky algorithm, in which the balls are enlarged and moved more frequently than in the force-biased algorithm. There are also so-called molecular dynamics methods in which the size of the spheres does not change. Instead, they move according to Newton's laws of motion , bouncing off other spheres elastically. An example of such an algorithm is the SPACE algorithm.

Collective rearrangement algorithms are able to generate very dense packing of spheres.

Efficient methods

Separate methods for generating hard-core point fields were developed for computer graphics, since the speed of execution plays a major role here.

Bridson's method

Bridson described an algorithm with linear time complexity as a function of the number of points. In contrast to many other algorithms commonly used in computer graphics, Bridson's algorithm is suitable for hard-core point fields in any dimensions.

The algorithm starts with a randomly chosen starting point that is added to a list of “active” points. A random reference point is then selected from the active list. Then a maximum number of candidate points (typically up to ) are randomly placed within the circular ring between δ and 2δ. If a candidate point is within the minimum distance to all previously retained points, it is added to the point field and added to the active list. If no candidate point adheres to the minimum distance after attempts, the reference point is removed from the active list. This process is repeated until the active list is empty. ${\ displaystyle k = 30}$ ${\ displaystyle k}$

The linear time complexity is achieved by dividing the area or space into a regular grid. The side length of the cells is not selected to be greater than that, the number of dimensions being. As a result, each cell contains a maximum of one point, so that only neighboring cells have to be searched when checking for compliance with the minimum distance. Such a distribution scheme can also speed up many of the algorithms described above. ${\ displaystyle \ delta / {\ sqrt {n}}}$ ${\ displaystyle n}$

The pseudocode of the algorithm (here without the distribution scheme) is as follows:

Punktfeld ← (leer)
AktiveListe ← (leer)
Ausgangspunkt ← ξ
Füge Ausgangspunkt zu Punktfeld hinzu
Füge Ausgangspunkt zu AktiveListe hinzu
 
Wiederhole solange AktiveListe ≠ (leer)
  Referenzpunkt ← [zufälliger Punkt aus AktiveListe]
  PunktGefunden ← Falsch
  Wiederhole k mal
    Kandidat ← ZufälligerPunktInKreisring(Referenzpunkt)
    Für jeden Punkt in Punktfeld
       Wenn ||Punkt - Kandidat|| < δ
         Nächster Kandidat
    Füge Kandidat zu Punktfeld hinzu
    Füge Kandidat zu AktiveListe hinzu
    PunktGefunden ← Wahr
  Wenn PunktGefunden = Falsch
    Lösche Referenzpunkt aus AktiveListe

Dunbar and Humphreys method

Dunbar and Humphreys' algorithm also has a linear time complexity. As with Bridson's method, new points are added around the existing points. The area available for new points, however, is represented more precisely by means of a special data structure, the “grooved circle sector”. This allows the hard-core point field to be generated very efficiently.

Tiling

Instead of generating a hard-core point field for the entire area, several small tiles with individual point fields can be created and then put together. Several such methods have been developed using either square tiles or Wang tiles . In order to maintain the minimum distance as well as possible at the edges of the tiles, the tiles can have periodic boundary conditions or certain points can be moved depending on the composition of the tiles.

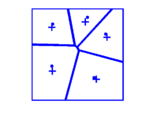
Lloyd algorithm

The Lloyd algorithm can be used to increase the minimum distance of an existing (hard-core) point field. The Lloyd algorithm is based on the Voronoi diagram of the point field and shifts the points in the direction of the centroid of their Voronoi cell. This process is repeated gradually. For two-dimensional point fields, the Lloyd algorithm converges to 75 to 85% of the maximum packing density.

The pictures below show a point field after 1, 2, 3 and 15 steps of the Lloyd algorithm. The crosses mark the focus of the Voronoi cells.

literature

AD Cliff, JK Ord: Spatial processes: models & applications, p. 103 f. Pion, London 1981, ISBN 0-85086-081-4
Peter J. Diggle: Statistical analysis of spatial point patterns, pp. 60 ff. Academic Press, London 1983, ISBN 0-12-215850-4
Janine Illian: Statistical analysis and modeling of spatial point patterns, pp. 387-397. Wiley, Chichester 2008, ISBN 978-0-470-01491-2
Ares Lagae, Philip Dutré: A comparison of methods for generating Poisson disk distributions. Computer Graphics Forum, 27, 1 (March 2008): 114–129, ISSN 0167-7055 ( PDF, 910 kB )
Dietrich Stoyan: Simulation and characterization of random systems of hard particles. Image Analysis and Stereology 21 (Dec. 2002): 41–48, ISSN 1580-3139 ( PDF, 3.7 MB )
Dietrich Stoyan, Joseph Mecke: Stochastic Geometry: an introduction, pp. 87-90. Akademie-Verlag, Berlin 1983, ISSN 0084-098X
Dietrich Stoyan, Wilfried S. Kendall, Joseph Mecke: Stochastic geometry and its applications, pp. 162–166. Wiley, Chichester 1995, ISBN 0-471-95099-8

Individual evidence

^ Alfréd Rényi: On a one-dimensional problem concerning random space-filling. A Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei 3 (1958): 109–127, ISSN 0541-9514
^ Bertil Matérn: Spatial variation. Meddelanden från Statens Skogsförsöksanstalt 49 (1960): 1–144, ISSN 0369-2167 . See also Bertil Matérn: Spatial variation (= Lecture Notes in Statistics 36), p. 47 ff.Springer, Berlin 1986, ISBN 3-540-96365-0
↑ Jesper Møller, Mark L. Huber, Robert L. Wolpert: Perfect simulation and moment properties for the Matérn type III process. Stochastic Processes and their Applications 120, 11 (Nov. 2010): 2142–2158, ISSN 0304-4149 ( PDF, 320 kB )
↑ Georges Matheron: Schéma booléen séquentiel de partition aléatoire. Note géostatistique N ° 89, Center de Morphologie Mathématique, École des Mines de Paris, Fontainebleau 1968 ( PDF, 550 kB )
↑ Wilfrid S. Kendall, Elke Thönnes: Perfect simulation in stochastic geometry. Pattern Recognition 32 (1999): 1569–1586, ISSN 0031-3203 ( ps.gz, 420 kB )
↑ W. Steven Jodrey, Elmer M. Tory: Simulation of random packing of spheres. Simulation 32, 1 (Jan. 1979): 1-12, ISSN 0037-5497
^ William M. Visscher, M. Bolsterli: Random Packing of Equal and Unequal Spheres in Two and Three Dimensions. Nature 239 (Oct. 27, 1972): 504-507, ISSN 0028-0836 . Quoted in Antje Elsner: Computer-assisted simulation and analysis of random close packing of spheres, p. 21. Dissertation, Technical University Bergakademie Freiberg 2009 ( PDF, 6.6 MB )
↑ WS Jodrey, EM Tory: Computer simulation of random close packing of equal spheres. Physical Review A 32 (1985): 2347-2351, ISSN 1050-2947
↑ Boris D. Lubachevsky, Frank H. Stillinger: Geometric properties of random disk packings. Journal of Statistical Physics 60, 5/6 (1990): 561-583, ISSN 0022-4715 ( PDF, 1.5 MB )
↑ Piet Stroeven, Martijn Stroeven: Reconstructions by SPACE of the interfacial transition zone. Cement and Concrete Composites 23, 8 (2001): 189-200, ISSN 0958-9465
^ Robert Bridson: Fast Poisson disk sampling in arbitrary dimensions. In ACM SIGGRAPH 2007 Sketches, Article 22. ACM, New York, 2007 ( PDF, 110 kB )
^ Daniel Dunbar, Greg Humphreys: A spatial data structure for fast Poisson-disk sample generation. In Proceedings of ACM SIGGRAPH 2006, pp. 503-508. ACM, New York 2006, ISBN 1-59593-364-6 ( online )
↑ See Lagae / Dutré for a comparison
↑ Stuart P. Lloyd: Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2 (March 1982): 129-137, ISSN 0018-9448 ( PDF, 1.2 MB )
↑ Lagae / Dutré, p. 6

[1] Alfréd Rényi: On a one-dimensional problem concerning random space-filling. A Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei 3 (1958): 109–127, ISSN 0541-9514

[2] Bertil Matérn: Spatial variation. Meddelanden från Statens Skogsförsöksanstalt 49 (1960): 1–144, ISSN 0369-2167 . See also Bertil Matérn: Spatial variation (= Lecture Notes in Statistics 36), p. 47 ff.Springer, Berlin 1986, ISBN 3-540-96365-0

[3] Jesper Møller, Mark L. Huber, Robert L. Wolpert: Perfect simulation and moment properties for the Matérn type III process. Stochastic Processes and their Applications 120, 11 (Nov. 2010): 2142–2158, ISSN 0304-4149 ( PDF, 320 kB )

[4] Georges Matheron: Schéma booléen séquentiel de partition aléatoire. Note géostatistique N ° 89, Center de Morphologie Mathématique, École des Mines de Paris, Fontainebleau 1968 ( PDF, 550 kB )

[5] Wilfrid S. Kendall, Elke Thönnes: Perfect simulation in stochastic geometry. Pattern Recognition 32 (1999): 1569–1586, ISSN 0031-3203 ( ps.gz, 420 kB )

[6] W. Steven Jodrey, Elmer M. Tory: Simulation of random packing of spheres. Simulation 32, 1 (Jan. 1979): 1-12, ISSN 0037-5497

[7] William M. Visscher, M. Bolsterli: Random Packing of Equal and Unequal Spheres in Two and Three Dimensions. Nature 239 (Oct. 27, 1972): 504-507, ISSN 0028-0836 . Quoted in Antje Elsner: Computer-assisted simulation and analysis of random close packing of spheres, p. 21. Dissertation, Technical University Bergakademie Freiberg 2009 ( PDF, 6.6 MB )

[8] WS Jodrey, EM Tory: Computer simulation of random close packing of equal spheres. Physical Review A 32 (1985): 2347-2351, ISSN 1050-2947

[9] Boris D. Lubachevsky, Frank H. Stillinger: Geometric properties of random disk packings. Journal of Statistical Physics 60, 5/6 (1990): 561-583, ISSN 0022-4715 ( PDF, 1.5 MB )

[10] Piet Stroeven, Martijn Stroeven: Reconstructions by SPACE of the interfacial transition zone. Cement and Concrete Composites 23, 8 (2001): 189-200, ISSN 0958-9465

[11] Robert Bridson: Fast Poisson disk sampling in arbitrary dimensions. In ACM SIGGRAPH 2007 Sketches, Article 22. ACM, New York, 2007 ( PDF, 110 kB )

[12] Daniel Dunbar, Greg Humphreys: A spatial data structure for fast Poisson-disk sample generation. In Proceedings of ACM SIGGRAPH 2006, pp. 503-508. ACM, New York 2006, ISBN 1-59593-364-6 ( online )

[13] See Lagae / Dutré for a comparison

[14] Stuart P. Lloyd: Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2 (March 1982): 129-137, ISSN 0018-9448 ( PDF, 1.2 MB )

[15] Lagae / Dutré, p. 6