Packing density (crystallography)
The packing density (also called packing ratio or space filling , English APF for atomic packing factor) is defined in crystallography as the ratio of the volume of the atoms in a unit cell to the total volume of the unit cell.
The term was adopted analogously in mathematics for spatial optimization problems , such as packing of spheres , which play a role in the theory of data compression.
Basics
The atoms are assumed to be hard, incompressible spheres of maximum and identical size. The numerical value of the packing density is characteristic of the type of packing. It does not depend on the conception of the unit cell (the spheres made up of two or more unit cells fill the same proportion of space as in a unit cell). Further conclusions about the shape of the lattice can be drawn from the space being filled and, for example, the stability or density of a crystal can be explained.
In general, the packing density results from:
where is the number of atoms (= the sum of the individual proportions) in the unit cell. The volume of the spheres in the unit cell with radius is calculated as follows:
In many crystal systems the unit cell is cubic. The volume of such a unit cell with the lattice parameter is:
For packing with a cubic unit cell the following applies:
Assuming only one type of atom with identical atom size, the greatest possible space filling is that of a cubic closest packing of spheres ( cubic face-centered lattice ) and the hexagonal closest packing of spheres . It is about 74%.
Crystal structure of elements
Most of the elements crystallize out in the packing types listed here.
Calculation of the space filling
Cubic Primitive Packing
In a cubic primitive packing (English: scp , simple cubic packing) the spheres occupy the 8 corners of the cubic unit cell. Since the alpha modification of polonium crystallizes in this type, it is often referred to by the common name α-polonium type .
Seen from above, one layer of this pack looks like this:
All layers of this type of packing are therefore identical. With its volume, each ball fills the volume in the surrounding unit cells. Each unit cell is filled with a spherical volume. Each ball touches 6 other balls directly, the coordination number is 6. All balls touch each other without gaps. The lattice parameter is twice the radius of the sphere :
So is
The packing density is about 52.36%
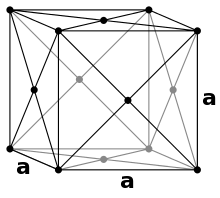
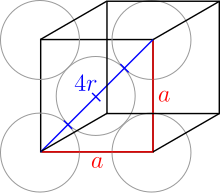
Face-centered cubic packing
In a face-centered cubic packing (English: fcc , face centered cubic) 8 spheres occupy the corners of a cubic unit cell and fill them with 1/8 of their spherical volume. In addition, there is a sphere in the middle of the 6 surfaces, which adds 1/2 of its volume to the unit cell. Thus there are 8 · 1/8 + 6 · 1/2 = 4 spheres in each unit cell . Since copper crystallizes in this type, it is also referred to as copper type .
The top and bottom layers are the same. Here the spheres touch along the diagonal of the unit cell:
The middle layer looks like this when viewed from above:
The balls on the corners therefore do not touch other balls on corners. The radius of all spheres is still the same. The Pythagorean theorem concludes:
So the radius is
The packing density is approximately 74.05%
Body-centered cubic packing
In a body centered cubic (also: body centered ) pack (English: bcc , body centered cubic) sit like 8 spheres on the corners of the cubic unit cell. The balls do not touch at the corners. In the middle of the unit cell sits a sphere, the entire volume of which is enclosed by the unit cell. So here there are 8 · 1/8 + 1 = 2 spheres in the unit cell. This type is referred to by the common name Wolfram-Typ .
The top and bottom layers look like this:
In the middle layer sits the full ball:
In this type, too, all balls have the same radius. The spheres touch each other along the space diagonal through the unit cell.
In order to calculate the room diagonal you need the area diagonal. So the Pythagorean theorem is applied twice:
and
The radius corresponds to:
The packing density is approximately 68%
Applications
With the knowledge of the packing, for example density, molar mass and much more. be calculated.
example
The density is an intensive quantity that does not depend on the size of the system under consideration. The density of one cubic meter of a metal is identical to the density of the unit cell of the structure of the metal. Knowing the lattice parameter , the molar mass and the number of atoms per unit cell, the density can e.g. B. of a metal can be calculated as follows:
Copper crystallizes in a cubic, densely packed lattice. So there are atoms in a unit cell. The radius of a copper atom is Å , which corresponds to .
The grid parameter for this type is calculated as follows:
The density of copper is:
Web links
- Calculations of the packing densities , Fachinformationszentrum Chemie Berlin (ChemgaPedia)
- Calculation of packing densities of different cubic crystal structures