Kepler's conjecture

from Wikipedia, the free encyclopedia
Face-centered cubic packing on the left, hexagonal packing on the right.

The Kepler conjecture is the conjecture expressed by Johannes Kepler that with the closest packing of spheres in three-dimensional Euclidean space, no arrangement of spheres of the same size has a greater mean density than the face-centered cubic packing and the hexagonal packing . Both packs have the same mean density of just over 74 percent.

In 1998 Thomas Hales announced that he had found evidence for Kepler's Conjecture. The computer evidence did not initially convince all mathematicians. The formal proof by Hales and co-workers published in 2017 has proven the Kepler Conjecture.

background

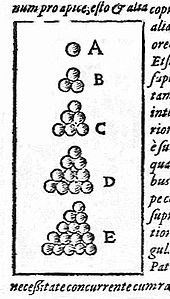
Imagine a large container with small balls of the same size. The density of the arrangement of the spheres is the proportion of the volume of the container that is occupied by the spheres. In order to maximize the number of balls in the container, one has to find the arrangement with the highest possible density so that the balls are packed as tightly as possible.

Experiments show that spilling the balls in randomly leads to a density of around 65 percent. However, a higher density can be achieved by arranging the spheres in the following way: Start with a plane spheres, which are arranged in a hexagonal grid. Then the next level is placed in the lowest points of the previous level, etc. In this way, z. B. Apples stacked in the market. This natural way of stacking the spheres results in an infinite number of possibilities, of which face-centered cubic packing and hexagonal packing are the best known and most common in nature. Each of these spherical packings has an average density of

(Follow A093825 in OEIS ).

The Kepler assumption states that these packings are the best possible - no packing can produce a higher density than this one.

history

Johannes Kepler (1610)

origin

Illustration from Strena seu de nive sexangula (1611)

The conjecture is named after Johannes Kepler , who set it up in 1611 in Strena seu de nive sexangula (About the hexagonal snowflake ) . In this paper, Kepler examined the mathematical construction principles of snowflakes, honeycomb cells and pomegranate seeds. He looked for a general theory of the self-structuring of nature and formulated not only the principle of the closest packing, but also the principle of the least effect. Based on his correspondence with the English mathematician and astronomer Thomas Harriot, Kepler began to study the arrangement of spheres in 1606. Harriot was a friend and assistant to Sir Walter Raleigh , who commissioned Harriot to investigate the problem of how best to stow the cannonballs on his ships. Harriot published a study of various arrangements of spheres in 1591 and developed an early version of the atomic model in the process .

19th century

Kepler had no proof of his guess. The first step towards a proof was taken by the German mathematician Carl Friedrich Gauß , who published a partial solution in 1831. Gauss proved that Kepler's Conjecture is true if the spheres have to be arranged in a regular grid .

This statement means that an arrangement of balls, which would refute Kepler's conjecture, would have to be an irregular arrangement. However, ruling out all possible irregular arrangements is very difficult, which makes proving the conjecture so difficult. In fact, it is known that there are irregular arrays that are denser than face-centered cubic packing in a small area, but any attempt to expand these arrays to a larger volume will decrease their density.

According to Gauss, no further progress was made in proving the Kepler conjecture in the 19th century. In 1900 David Hilbert added the problem to his list of 23 math problems - it is a special case of Hilbert's 18th problem.

20th century

The next step in solving the problem was taken by the Hungarian mathematician László Fejes Tóth . In 1953 Fejes Tóth proved that the problem of calculating the maximum of all (regular and irregular) arrangements can be reduced to considering a finite (but very large) number of cases. This meant that a proof was in principle possible through a very large case distinction. Fejes Tóth was the first to establish that, with the help of a sufficiently fast computer, this theoretical result can be converted into a practical approach to prove the conjecture.

In the meantime, attempts have been made to find an upper limit for the maximum density of all possible spherical arrangements. The English mathematician Claude Ambrose Rogers proved an upper limit of about 78 percent in 1958, and subsequent efforts by other mathematicians were able to reduce this limit slightly, but even this was still well above the face-centered cubic packing density of 74 percent.

There was also some failed evidence. The American architect Richard Buckminster Fuller claimed to have found evidence in 1975, but it soon turned out to be incorrect. In 1993 the Chinese-American mathematician Wu-Yi Hsiang published an essay at the University of Berkeley in which he claimed to prove Kepler's Conjecture by geometric means. Some experts disagreed, as he gave insufficient justification for some of his claims. Although nothing wrong per se was found in Hsiang's work (after the latter, however, steadily improved the preprints of his proof), there is a general consensus that Hsiang's proof is incomplete. One of the loudest critics was Thomas Hales, who was working on his own proof at the time.

Hales' proof

In 1998 Thomas Hales , currently Andrew Mellon Professor at the University of Pittsburgh , announced that he had found evidence for Kepler's Conjecture. Hales' proof is a case-discrimination proof, in which he examines many different cases using complex calculations on the computer .

Following Fejes Tóth's approach, Thomas Hales, at that time at the University of Michigan , determined that the maximum density of all spherical arrangements can be found by minimizing a function with 150 variables. In 1992, with the support of his PhD student Samuel P. Ferguson , he began a research program that uses linear optimization methods to determine a lower limit for this function applied to a set of over 5,000 spherical arrangements. If a lower limit for the function value were found for each of these spherical arrangements, which is greater than the function value for the face-centered cubic packing, then Kepler's conjecture would be proven. In order to determine the lower limits for all cases, more than 100,000 individual linear optimizations had to be calculated.

When Hales presented the progress of his work in 1996, he said the end was in sight, but it could still be "a year or two". In August 1998, Hales announced that the evidence was complete. At that point it consisted of 250 pages of records and three gigabytes of computer programs, data, and results.

Despite the unusual form of the evidence, Robert MacPherson , one of the editors of the prestigious mathematical journal Annals of Mathematics , suggested a publication in that journal. However, the assessment of the computer evidence had to meet the highest standards, so that the evidence was first presented to a panel of twelve experts. Gábor Fejes Tóth , the spokesman for the reviewers (and the son of László Fejes Tóth), announced in 2003, after four years of work, that the reviewers were "99 percent sure" that the evidence was correct, but they could not be correct certify all calculations performed on the computer. MacPherson then noted that the reviewers might have had it easier and would have come up with a clear answer if Hales' manuscript had been more readable and understandable. As a result of the expert opinion it is assumed that Kepler's conjecture could now become a mathematical proposition .

In May 2003 Hales published a hundred-page preprint article detailing the non-computer-computed portion of his proof. The Annals of Mathematics published the theoretical part of Hales' proof in 2005, which was successfully reviewed by the review panel. The results of the computer calculations - that is, a more complete publication in the form of the revision of the preprints from 1998 - were published in a specialized journal, Discrete and Computational Geometry .

Formal proof

In January 2003, Hales announced the start of a collaborative project to produce a fully formal proof of Kepler's conjecture. The aim of this project was to dispel any remaining doubts about the validity of the proof by using a computer to create a formal proof in Objective CAML , which is supported by interactive theorem provers such as B. John Harrison's HOL light can be checked. The project is called Project FlysPecK , where the F, P and K stand for Formal Proof of Kepler . Hales estimated that it would take about 20 years to produce the formal evidence. In August 2014, he announced that the evidence had been successfully transferred into computerized form and that the software had confirmed the accuracy of the evidence.

In January 2015 Hales and 21 co-authors published a paper with the title A formal proof of the Kepler conjecture on the preprint server arXiv , and claimed to have proven the assumption. In 2017 the proof was published in the journal Forum of Mathematics, Pi .

literature

Web links

Individual evidence

  1. ↑ Marie-Luise Heuser , Kepler's theory of the self-structuring of snowflakes against the background of Neoplatonic philosophy of mathematics, in: Self-organization. Yearbook for Complexity in the Natural, Social and Human Sciences, ed. v. Uwe Niedersen, Vol. 3: Concepts of chaos and self-organization in the history of science, Berlin (Duncker & Humblot) 1992, pp. 237-258.
  2. ^ Thomas C. Hales: A computer verification of the Kepler conjecture . In: arXiv: math / 0305012 . April 30, 2003 (arXiv = math / 0305012 [accessed March 18, 2019]).
  3. ^ A proof of the Kepler conjecture | Annals of Mathematics. Retrieved March 18, 2019 (American English).
  4. ^ Thomas C. Hales, Samuel P. Ferguson: A Formulation of the Kepler Conjecture . In: Discrete & Computational Geometry . tape 36 , no. 1 , July 2006, ISSN  0179-5376 , p. 21-69 , doi : 10.1007 / s00454-005-1211-1 ( springer.com [accessed March 18, 2019] Other articles by Hales, Ferguson in the same issue).
  5. ↑ derStandard.at - Proof of a 400 year old stacking problem confirmed . Article dated August 15, 2014, accessed August 16, 2014.
  6. ↑ Thomas Hales, Mark Adams, Gertrud Bauer, Tat Dat Dang, John Harrison: A formal proof of the Kepler conjecture . In: Forum of Mathematics, Pi . tape 5 , 2017, ISSN  2050-5086 , doi : 10.1017 / fmp.2017.1 ( cambridge.org [accessed March 18, 2019]).