Focal length
The focal length is the distance between the main plane of an optical lens or a curved mirror and the focus (focal point).
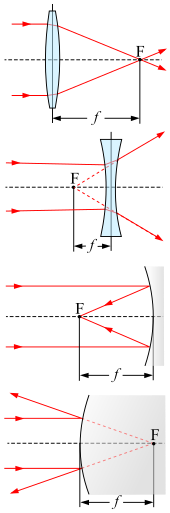
- A converging lens concentrates a parallel incident beam in the focal point lying after it (figure on the right, first image).
- In the case of diverging lenses , the focus is in front of the lens and a bundle of rays incident in parallel is scattered as if the individual rays all came from this focus (second image).
- In the case of a concave mirror , a parallel incident bundle of rays converges at the focal point in front of the mirror (third image).
- In the case of a convex mirror , a parallel incident bundle of rays is scattered as if the individual rays all came from the focus behind the mirror (fourth image).
Systems consisting of several lenses and / or mirrors - such as the lenses of cameras or microscopes - have focal lengths that are defined analogously. The positions of the main planes (two per system) cannot be specified as easily as with a single lens (in it) or with a single mirror (on its apex).
The focal length is a concept of paraxial optics . It therefore only relates to rays that have a small angle and a small distance from the optical axis of the imaging system.
Large focal lengths are created by flat, slightly curved surfaces. Small focal lengths are caused by strong curvatures. Especially with individual lenses, the reciprocal of the focal length becomes the refractive power or called the refractive index . For converging lenses and concave mirrors , the focal length is defined as a positive value, for diverging lenses and convex mirrors as a negative value.
The focal length is used when applying the lens equation . In photography , the focal length of the lens and the recording format determine the angle of view (see also format factor ). This also applies to the intermediate image on the microscope . With telescopes and binoculars, the focal lengths of the objective and eyepiece together determine the magnification .
Refractive power
The reciprocal of the focal length is called the refractive power . It is given in diopters for spectacle lenses .
Measurement of the focal length
According to the imaging equation , with a sharp optical image through a thin lens, the reciprocal of the focal length is equal to the sum of the reciprocal values of the object distance and the image distance :
This can be used to determine the focal length of the lens. If the object depicted is very far away, the connection becomes particularly simple. The focal length is approximately the same as the image distance and can be read directly from the distance between the image and the lens.
One method that works without a distant object is autocollimation . The distant object is replaced by a flat mirror. The Bessel method for determining the focal length of thin lenses takes advantage of the fact that with a fixed distance between the object and the image, two positions of the lens produce a sharp image. The focal length of the lens can then be calculated from the distance between these two positions and the distance between the object and the image.
In the case of thick lenses and imaging systems with several optical components, the distance between the main planes can usually not be neglected. Then estimating the magnification ratio can provide more accurate results. The Abbe method is used to record a set of positions in which the imaging system images objects in focus. These points satisfy a straight line equation . The focal length and the position of the main planes can be determined from the parameters of the straight line.
Opticians use a wavefront analysis to determine the focal length of aspherical lenses and the refractive power of varifocal lenses, which varies over the surface . A Hartmann Shack sensor is usually used for this. For historical reasons, the automated devices are called lens meters .
Calculating the focal length
Breaking surface
The boundary layer between two optical media with different refractive indices is called the refractive surface. If the light beam comes from the left, then the refractive index is on the left side and the refractive index on the right side of the interface. The curvature of the interface is described by the radius of curvature . If the center of the circle that describes the interface is on the side facing away from the incident light, then it is positive, otherwise it is negative. A non-curved interface has the radius of curvature .
The focal length of the other side is obtained by changing the refractive indices, since the light now coming from the right after transgresses:
lens
The refraction of a lens of thickness is e.g. B. by means of matrix optics , can be calculated from the refractions of their two spherical interfaces. With the focal lengths and the two surfaces and their distance results
for the image-side focal length of the lens. With the above equations of the surface focal lengths one obtains with
the lens focal length on the image side as a function of the radii of curvature and the refractive indices and . As in the adjacent figure, the focal length is measured from the main plane H '. Object-side and image-side focal lengths have the same size if the lens is adjacent to media with the same refractive index on both sides , see also lens grinder formula .
Thin lens
The approximation is fulfilled for. This approximation is known as a thin lens, and the main planes of the two interfaces coincide (namely to the median plane ). The equation for the focal length simplifies to
measuring away from the center plane again.
In geometrical optics, the term front surface power and rear surface power. The above equation can thus also be expressed in the form
write. The optical effect of eyeglass lenses is expressed by the vertex power .
System of two thin lenses
The system of two thin lenses is basically similar to the system “lens made of two refractive surfaces” (cf. adjacent figure with the one above). If both lenses are surrounded by the same medium on both sides, then:
In addition to the equality of the object and image-side focal lengths of the individual lenses, the corresponding equality also applies to the system:
The dependence of the focal lengths of the lens system consisting of two thin lenses on the refractive indices and radii of curvature is obtained if the lens grinding formulas given above for thin lenses are used for and .
Thin lenses closely spaced
When moving the thin lenses together, in the borderline case . The distance can be neglected. The focal length of such a system is approximately the same
This equation is used for two thin lenses cemented together, for example. Such a double lens usually consists of two different types of glass , with which lower imaging errors are achieved than with a lens consisting of only one type of glass with the same focal length, such as with the achromatic lens .
Image errors with a direct connection to the focal length
Strictly speaking, the focal length is only defined in paraxial optics. However, under certain conditions and above all for real non-parabolic lenses, various so-called imaging errors arise, which result in a (sometimes seemingly) changed focal length.
In paraxial optics it is always possible to approximate a spherical surface as a paraboloid . Real lenses are often designed as spherical surfaces, as these are easier to manufacture than aspherical surfaces . You are still assigned a focal length that actually only applies to rays close to the optical axis. For off-axis rays, shifted foci result. This lens defect is called spherical aberration .
Furthermore, the focal length depends, among other things, on the refractive index of the lens material, which in turn depends on the wavelength of the light. If light of different wavelengths (e.g. also white light) falls on a lens, this is focused on different points depending on the wavelength. One speaks of chromatic aberration .
If the shape of a lens is not rotationally symmetrical with respect to the optical axis, but rather ellipsoid , then it focuses fan-like light bundles depending on their orientation in different image distances. Full bundles of light are not focused on one point, but rather in two consecutive focal lines in the directions of the two main axes of the ellipsoid. This aberration is called axial astigmatism .
See also
literature
- Max Born: Optics. 1972, ISBN 3-540-05954-7 (2nd chapter).
- Fritz Hodam: Technical optics. 1967.
- Wolfgang Demtröder : electricity and optics. Springer, Berlin 2006. ISBN 3-540-33794-6 (Chapter 9.5)
Web links
Individual evidence
- ↑ Eugene Hecht: Optics. Oldenbourg Verlag, Chapter 5 Geometrical Optics. Section 2 lenses.
- ^ Ophthalmic lens compendium. ( Memento from July 3, 2013 in the web archive archive.today ). At: Zeiss.de.
- ^ Wolfgang Demtröder : Electricity and optics. Springer, Berlin 2006. ISBN 3-540-33794-6 (Chapter 9.5.4).