Magnification (optics)

The magnification of an optical instrument is the ratio between the apparent size (size of the image) and the true size of an object.

• In the case of optical instruments with a view into an eyepiece , “size” is to be understood as the viewing angle (viewing angle), which is then referred to as angle magnification .
• If the image appears on a screen, the "size" is a measure of length and can be measured with a ruler; this is then referred to as linear magnification . The magnification in the direction transverse to the optical axis is called the lateral magnification, the magnification along the optical axis, which is decisive for the depth of field , is called the axial magnification .

In all of these cases the magnification is a dimensionless number , i.e. it has no physical unit .

Angle enlargement

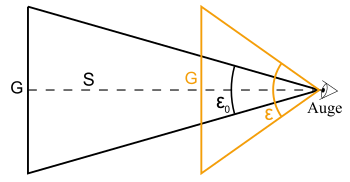
The magnification (sometimes called) of an optical instrument that one looks into with the eye is by definition: ${\displaystyle V}$ ${\displaystyle \Gamma }$

${\displaystyle V={\frac {\tan \varepsilon }{\tan \varepsilon _{0}}}}$

${\displaystyle \varepsilon _{0}}$is the viewing angle at which you can see an object without optical aids (shown in black). This angle depends on the distance between the eye and the object; the closer the object, the greater the viewing angle. In the case of magnifying glasses and microscopes, a distance of is therefore assumed by convention at which the object can still be seen clearly without optical aids ( clear visual range ). ${\displaystyle G}$ ${\displaystyle S}$ ${\displaystyle S:=250\,\mathrm {mm} }$

${\displaystyle \varepsilon }$is the viewing angle at which the object appears in the optical instrument (shown in orange). The greater the viewing angle , the greater the eye sees the object. ${\displaystyle \varepsilon }$

Magnifying glass

Formally, the magnification is calculated as follows:

${\displaystyle V={\frac {\tan \varepsilon }{\tan \varepsilon _{0}}}={\frac {\frac {G}{f}}{\frac {G}{250\,\mathrm {mm} }}}={\frac {250\,\mathrm {mm} }{f}}}$

where 250 mm corresponds to the clear visual range and the object lies in the focal plane.

See also : "Determining the magnification" in the article Magnifying glass

microscope

The magnification of a microscope is the product of the magnification of the objective and the magnification of the eyepiece . ${\displaystyle V_{\mathrm {Ob} }}$ ${\displaystyle V_{\mathrm {Ok} }}$

${\displaystyle V=V_{\mathrm {Ok} }\cdot V_{\mathrm {Ob} }}$

The magnification of the lens is calculated from ${\displaystyle V_{Ob}}$

${\displaystyle V_{\mathrm {Ob} }={\frac {d-f_{\mathrm {Ob} }}{f_{\mathrm {Ob} }}}}$,

where is the focal length of the objective and the distance from the objective to the focal plane of the eyepiece. Under the magnification of the objective which is usually magnification understood. The enlargement of an objective does not mean an angle enlargement . A prerequisite for the calculation is that the objective is used in the way it is intended for in the associated microscope. This means that the distance to the object is chosen so that the intermediate image is created where the focal plane of the eyepiece is in the microscope (or a CCD camera in newer microscopes). The distances from the two main planes of the eyepiece to the object and to the intermediate image are determined by the lens equation . In microscope systems with interchangeable objectives, the connection between the objectives and the microscope tube is usually adjusted so that the optical tube length , i.e. the distance between the objective focal point facing the eyepiece and the intermediate image plane , remains constant for different objectives. As a result, the magnification of the objective can be calculated very easily, namely as ${\displaystyle f_{\mathrm {Ob} }}$ ${\displaystyle d}$

${\displaystyle t:=d-f_{\mathrm {Ob} }}$

${\displaystyle V_{\mathrm {Ob} }={\frac {t}{f_{\mathrm {Ob} }}}}$

An optical tube length between . ${\displaystyle t=160\,\mathrm {mm} {\text{ und }}200\,\mathrm {mm} }$

The magnification of the eyepiece is like that of a magnifying glass

${\displaystyle V_{\mathrm {Ok} }={250\,\mathrm {mm} }/f_{\mathrm {Ok} }}$

given. Just like the total magnification of a microscope, it corresponds to an angular magnification .

Kepler's telescope

The magnification of a telescope (astronomical telescope or binoculars with erecting prisms) is through

${\displaystyle V={\frac {f_{\mathrm {Ob} }}{f_{\mathrm {Ok} }}}}$

given. Here and are the focal lengths of the lens or eyepiece. ${\displaystyle f_{\mathrm {Ob} }}$ ${\displaystyle f_{\mathrm {Ok} }}$

In order to be able to use the calculated magnification, however, the opening (objective diameter, aperture ) and the exit pupil of the telescope must also be selected appropriately:

• On the one hand, the exit pupil of the telescope should not be larger than the diameter of the pupil of the eye (2 to 8 mm, depending on the light conditions), since the eye can only evaluate the light that enters through the pupil.
• Since, on the other hand, the observed solid angle is reduced by the enlargement , the objective diameter must be increased accordingly so that the same light intensity reaches the eye.

In order to obtain the same brightness as with the unenlarged visual impression, the objective diameter must be larger than the pupil diameter of the eye as a first approximation by the factor of magnification. If the lens diameter is below this value, the enlarged image appears darker to the viewer (and may therefore no longer be easy to evaluate); in the opposite case, the enlarged image is brighter than the non-enlarged one (and thus may blind the viewer) . However, the latter effect is often used - especially in astronomy - to be able to view low-light situations well.

Concave mirror

If the concave mirror is used to look at one's own mirror image, i.e. as a cosmetic mirror, the magnification compared to a plane mirror with the same viewing distance is a maximum of 2 times (both mirrors at a distance of the focal length of the concave mirror). However, if the plane mirror is positioned so close that the mirror image can just be seen clearly, the concave mirror at a distance increases by the factor . This magnification can be increased slightly by reducing the distance to the concave mirror. ${\displaystyle f}$ ${\displaystyle V=250\,\mathrm {mm} /f}$

Limits of magnification

The magnification of an optical instrument can theoretically be increased as required by the choice of the lens and eyepiece focal lengths, but the resolution is limited under optimal conditions by the diffraction of light, one speaks of diffraction limitation. This "soft" limit for the maximum sensible magnification can be approximated as the diameter of the opening of the instrument in millimeters . Only enlargements below this value are called useful enlargements, since an increase in the enlargement makes smaller structures visible only within this range. If the magnification is increased above this value, no additional structures tend to be visible, but rather artifacts appear at best. B. Stars not as points, but as disks, which are surrounded by concentric circles (diffraction rings), one therefore speaks of dead magnification.

Under real conditions, imaging errors and, in the case of telescopes, the turbulence in the air (“ seeing ”) limit the maximum usable magnification even further. Although the image can possibly still be greatly enlarged without the theoretical diffraction limitation occurring, it becomes increasingly blurred in the process, so the image information remains practically the same despite greater magnification.

literature

• Eugene Hecht: optics . Oldenbourg Verlag, 4th edition 2005, ISBN 3-486-27359-0

Individual evidence

1. ↑ J. Hattenbach: The enlargement of one's own reflection in the cosmetic mirror
2. ↑ Joachim Krautter et al: Meyers Handbuch Weltall, Meyers Lexikonverlag, 7th edition 1994, ISBN 3-411-07757-3 , p. 553