Reproduction scale

The image scale (symbol ) is defined as the ratio between the image size of the optical image (y ', image) of an object and its real object size (y, object). Alternatively, the image scale can also be determined via the ratio of image distance a 'to object distance a: ${\ displaystyle \ beta}$

${\ displaystyle \ beta = {\ frac {y '} {y}} = {\ frac {a'} {a}}}$

For y = 1 or for y '= 1, it is often common to specify the magnitude of the reproduction scale as the ratio 1: y or y': 1.

An image scale with the amount 1 indicates that the object and its image are the same size.
An image scale with the amount 0.5 says that the object is twice as large as its image.
An image scale with the amount 2 says that the image is twice as large as the object.

photography

In the photography is referred to as imaging scale the magnitude of the ratio of the image size of an object on the image plane to the size of the original object itself. The magnification increases the with decreasing distance to the object and with extension lens focal length to.

Due to the close focus limit (the minimum distance to the object), below which it is no longer possible to focus on the object, the object distance cannot be reduced as desired.

Special lenses for macro photography , the so-called macro lenses , can be used with a particularly small object distance and thus enable a particularly large image scale, such as 0.5 (the image is half the size of the object) or 1 (object is in Original size shown in the image plane). With an image scale of at least 0.25, an objective is called macro-capable . Normal lenses achieve maximum reproduction ratios in the range from 1: 7 to 1: 9.

A special lens introduced by Minolta in the early 1990s , the Minolta AF Macro Zoom 3x – 1x (1: 1.7–1: 2.8) , even enables an image ratio of 3; it can therefore map an object three times enlarged in the image plane. In order to achieve such image scales without special lenses, a bellows device , intermediate rings and, in addition, a lens in retro position must be used to avoid color errors .

Examples for calculating the reproduction scale:

If the camera images a 20 cm high head in the image plane with a height of 0.5 cm, the magnitude of the image scale is 0.5: 20 = 1:40 = 0.025
If a 36 millimeter long insect is depicted on 35mm film with an image width of 36 millimeters, this means that the image scale is 1

The manufacturers of interchangeable lenses often fail to specify the image scale that can be achieved with a particular lens; instead, often only the shortest possible object distance is given. However, this information only allows an indirect conclusion about the effectively achievable image scale, especially since many lenses with camera housings of different image sensor sizes can be used. However, the reproduction scale can be determined with test images.

Spatial motifs

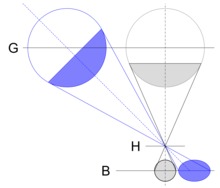
Distortion in the optical imaging of a sphere in the object plane G via the main plane H into the image plane B.

Spherical light source captured from a very short distance with a distortion- free ultra-wide angle lens . The right edge of the figure of the sphere is in the center of the picture, the left edge of the sphere is on the left edge of the picture. Due to the aspect ratio of 2: 1, it can be clearly seen that the width of the sphere shown is significantly greater than its height, so that its edge appears elliptical .

When imaging spatial objects, the imaging scale varies with the object width . The resulting geometric effects are not aberrations of the lenses used .

This can lead, for example, to parallel object edges being mapped as non-parallel converging lines .

The rays from the circular edge of a sphere , the center of which is not on the optical axis , are inevitably detected with different object widths in an optical image and therefore have different image scales in the image , which lead to a geometric distortion of the circular shape in the image. The object points which are closer to the optical axis are further away than the object points which are further away from the optical axis. Therefore, the greater the image scale, the further the image points are on the edge of the image. Especially when using wide-angle lenses , this can lead to clearly recognizable deformations in the images due to the large image angles .

Relative image scale

The relative image ${\ displaystyle m _ {\ text {rel}}}$ scale is defined as the ratio of the scale of an optical image with the focal length to the scale for an optical image with the normal focal length : ${\ displaystyle m}$ ${\ displaystyle f}$ ${\ displaystyle m _ {\ mathrm {N}}}$ ${\ displaystyle f _ {\ mathrm {N}}}$

{\ displaystyle m _ {\ text {rel}} = {\ frac {m} {m _ {\ mathrm {N}}}}}

At the same time, for large distances of the objects depicted (the object distance is significantly greater than the focal length ), the relative image scale is also approximately given by the following expression: ${\ displaystyle f}$

{\ displaystyle m _ {\ text {rel}} = {\ frac {f} {f _ {\ mathrm {N}}}}}

literature

Gottfried Schröder: Technical photography: Basics and applications in technology and science , Vogel-Druck, Würzburg, 1st edition, 1981

Web links

Wiktionary: Illustration scale - explanations of meanings, word origins, synonyms, translations

Image scale, Wikibook digital imaging methods (2013)

Individual evidence

↑ ^a ^b See DIN 4522-7: 1991-04 and DIN 1335: 2003-12
↑ Helmut Naumann, Gottfried Schröder, Martin Löffler-Mang: Handbook components of optics: Fundamentals, materials, devices, measuring technology , Carl Hanser Verlag, 2014, ISBN 9783446441156
↑ Spatial motifs , in: Digital imaging methods - image recording , accessed on October 26, 2018

[DIN-1] See DIN 4522-7: 1991-04 and DIN 1335: 2003-12

[2] Helmut Naumann, Gottfried Schröder, Martin Löffler-Mang: Handbook components of optics: Fundamentals, materials, devices, measuring technology , Carl Hanser Verlag, 2014, ISBN 9783446441156

[3] Spatial motifs , in: Digital imaging methods - image recording , accessed on October 26, 2018