Distortion
The distortion , often mistakenly also (optical) distortion called, is a geometric aberrations of optical systems in the lens equation to a local change in the image scale leads. The change in scale is based on a change in magnification with increasing distance of the image point from the optical axis. The distortion is therefore rotationally symmetrical around a point of the point of symmetry of the distortion, which is also called the center of the distortion. The cause of the distortion is caused by diaphragms or limiting lens diameters, which narrow the beam of the image in front of or behind the main plane of an optical system with aperture errors. This means that parts of the beam available for constructing the beam path are masked out. This changes the direction of the main ray - compared to an optical system without a diaphragm - and causes the distortion.
If the magnification increases towards the edges of the image field, a square is drawn in the shape of a pillow . In the opposite case one speaks of barrel-shaped distortion . Distortions of a higher order can also occur, and the superposition of different orders can lead to a wave-like image of straight lines (“wave-like distortion”).

In the case of optical devices for everyday use, the distortion is often not a noticeable disadvantage and may therefore be accepted. For example, glasses for nearsighted people have a strong barrel-shaped distortion towards the edge.
In devices with several lenses, such as telescopes , the distortion can be kept low by optical correction:
- Use of differently curved and differently thick lenses
- Glass types ( crown glass , flint glass ) with different refractive indices for the individual lenses.
These distortion-free optics are called orthoscopic lens systems . With optics used visually, however, it is not uncommon for a pillow-shaped distortion to be intentionally implemented in order to eliminate the annoying globe effect .
If photographic images are used for precise measurements, correspondingly corrected lens systems can be used, such as telecentric lenses . In addition, the remaining distortion can be determined by measurement and compensated for by calculation when evaluating the image .
The distortion of a lens should not be confused with the perspective distortion . The perspective distortion comes from the fact that a scene is viewed at an angle and aspect ratios (angles) are lost. In this way, a flat square that is viewed obliquely from any central perspective is distorted into a general square.
compensation
Methods have been developed especially for image measurement in photogrammetry to model and calculate the distortion of a lens .
By inverting these models, one can compensate for the actual distortion of an image and calculate a distortion-free image. In the case of barrel-shaped distortion, the rectified image becomes larger and, in the case of pincushion-shaped distortion, it becomes smaller if the image scale remains unchanged in the center of the image. With barrel rectification, some software keeps the original aspect ratio and cuts off useful image information at the edge, although a larger, undistorted and rectangular image would be possible.
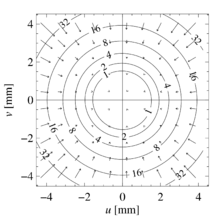
The picture on the right shows the distortion of a lens with a focal length of 20 millimeters when focusing at an object distance of one meter. The numbers on the isolines indicate the amount of compensation in micrometers. The length of the arrows is fifteen times the length of the change. The coordinates and are the image coordinates in relation to the center of the image.
Digital camera systems , such as the Micro Four Thirds system , can transfer individual properties of lenses, such as the characteristic data of the distortion, to the camera housing, which enables automatic digital compensation of this geometric imaging error in the camera or during the subsequent image processing .
Mathematical procedure
In the following text, the radius denotes the distance of an image point (on the sensor) from the optical axis.
In a perfect lens, the radius remains unchanged and we have: .
A common description for the radially symmetrical distortion is the polynomial or equivalent .
In fisheye lenses , the incident angle can be greater than 180 ° and the radius would be infinitely large: .
Therefore, the angle is here directly as a cubic function represented: .
Application examples
In photography, distortion is often used deliberately as an artistic instrument. The distortion effect is deliberate , especially with fisheye lenses .
In television , it is often undesirable for viewers to be able to see the real spatial extent of a studio. That is why many studios - e.g. B. at ZDF in Mainz - built with arched walls or even circular. Wide-angle lenses are then predominantly used. Their distortion is not a problem - it is more likely to be perceived unconsciously. At the upper edges of the walls - the only “mark” for the size of the room for spectators - the lens distortion cannot be distinguished from the “real” curvature; the wall appears "endless".
In the film and video sector, anamorphic distortions in widescreen format are brought about in a targeted manner using special camera and lens systems. Originally, anamorphic process was used to enable widescreen format in the cinema without changes to the usual 35 millimeter film material in the standard film format. The widescreen picture was squeezed by targeted distortion when recording a film - and rectified again by opposing lens arrangements when playing back in the cinema. This introduced the age of wide screen cinema - without the complete replacement of the existing camera and projection technology.
But not only the aspect ratio was influenced with anamorphic technology: A cinematic touch was created that has been considered state-of-the-art technology to date. Many cinematic effects are based on anamorphic lenses and create the "cinelook": reduced depth of field for better separation of the foreground and background, oval-shaped light effects ( bokeh ), distorted widescreen display, oval light reflections in rainbow colors, striped glare, overexposure and intentional distortion used as artistic tools.
literature
- DIN ISO 9039: Optics and photonics - Quality assessment of optical systems - Determination of distortion. (ISO 9039: 2008)
- DIN 58187: Quality assessment of optical systems - Determination of radial distortion. (June 1986)
- Fritz Deumlich, Rudolf Staiger: Instrumentenkunde der Vermessungstechnik , 9th edition, Wichmann, Heidelberg, 2001, ISBN 3-87907-305-8 .
- Karl Kraus: Photogrammetry . de Gruyter, 2004, ISBN 3-11-017708-0 .
- Harry Paul: Lexicon of Optics , Spectrum Academic Publishing House, Heidelberg 2003, ISBN 3-8274-1422-9 .
Web links
- B. Hönlinger and HH Nasse: Verzeichen , zeiss.com from October 2009
See also
Individual evidence
- ↑ Distortion , Wikibooks Digital Imaging Methods , Chapter Image Acquisition , accessed on September 16, 2015.
- ^ Richard Butler: A distorted view? In-camera distortion correction , dpreview.com, September 2, 2011, accessed January 23, 2016.