Depth of field

Only a small area of ​​the image appears sharp - an example of a shallow depth of field.

35mm camera with the option of reading the depth of field on the distance ring depending on the f-number (here at a distance of 2 m and a f-number 2.8 between ≈1.8 and ≈2.3 m.)

Three APS film boxes at different f-stops (f / 2.8 - f / 4 - f / 5.6 - f / 8 - f / 11 - f / 16)

The clipping of an object through shallow depth of field using the example of a single cyclist who is lifted out of the group

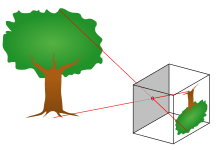
The depth of field (often also called depth of field ) is a measure of the extent of the sharp area in the object space of an imaging optical system . The term plays a central role in photography and describes the size of the distance range within which an object is shown sufficiently sharp. As a rule, a large depth of field is achieved through small aperture openings or lenses with short focal lengths : everything looks more or less sharp from front to back. The opposite is the so-called “film look”, in which the depth of field is small ( shallow ): the camera draws the central figure in focus, possibly only a person's eye, while everything in front of and behind it appears blurred. Deep in sharpening means deep , the depth of the space , that is the direction away from the optics .

The depth of field is influenced not only by the choice of focal length and the distance setting but also by the aperture : the larger the aperture (small f-number ), the smaller the depth of field (and vice versa). When setting the distance (focusing) on ​​a close object, the object space that is optically recorded as sharp is from – to shorter than when focusing on an object further away. Choosing the aperture is part of the exposure setting .

In computer animation , the depth of field is an optical effect that is calculated in retrospect in each individual image and therefore means considerable computational effort . Usually the term depth of field (DOF) is used here.

Colloquially, depth of field and depth of field are used synonymously. The term “depth of field” was standardized for the first time in 1970 (DIN 19040-3). The image depth represents the counterpart to the depth of field of the image side.

Geometric depth of field

There are basically two different arrangements to be distinguished: the camera obscura , which only consists of a single pinhole diaphragm , and a lens system, which also contains such a diaphragm, but also (at least) one lens (in front of or behind the diaphragm), the one produces regular optical imaging .

Camera obscura

Camera obscura

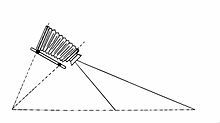
→ Main article : Camera obscura

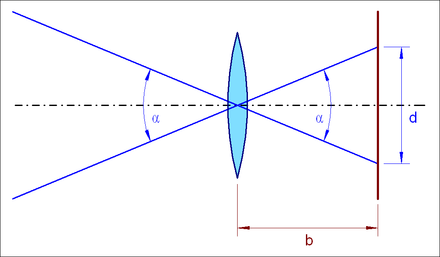
Light rays emanating from an object fall through the pinhole onto the image plane (a screen, a film or a camera image sensor). Depending on the diameter of the diaphragm, these light rays become more or less thick, conical light bodies. By intersecting the image plane with a cone, a circle is created on the plane, so-called circles of confusion or circles of blurring (Z). They exist for every dimensioning of the distances between object, aperture and image, the circle size in the image plane is calculated according to the ray theorem . The influence of the aperture diameter is simply proportional : the larger the hole, the larger the blur circle. A smaller hole is required for a sharper image. However, if the hole is reduced too much, the area of geometric optics is left and the wave properties of light come to the fore. The diffraction effects that occur become stronger the smaller the hole is. This leads to a decrease in sharpness . This means that there is an optimal hole diameter for a camera obscura. In addition to the imaging properties, this optimization must also take into account the fact that the smaller the hole diameter, the lower the luminous flux and thus the longer the exposure times .

Lens system

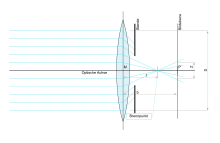
An additionally built-in lens ensures that, in the ideal case, a sharp image occurs at a certain distance between the image plane and the lens. In this position, the above inaccuracy does not apply and the aperture can be significantly enlarged in the interest of better light yield. Only when it comes to object points that are in front of or behind this sharply mapped position does this sharpness decrease and, with increasing distance, decrease to the value that the aperture alone would cause as a camera obscura. More accurate:

In geometrical optics , only those points can be reproduced as sharp image points in the image plane (film, chip) that lie on the plane that is within the object distance of the lens. All other points that are located on planes that are closer or farther away no longer appear in the image plane as points, but as discs, so-called circles of confusion or blurring (Z).

Circles of confusion arise because the light bodies falling from the lens onto the image plane (the film) are cones. By intersecting the image plane with a cone, a circle is created on the plane. Points lying close to one another that are not in the plane of the object are depicted by closely spaced circles of confusion that overlap and mix in the edge areas, creating a blurred image.

The maximum tolerable circle of confusion diameter for a camera for the acceptance of sharpness is denoted by Z. The absolute size of the maximum circle of confusion Z depends on the recording format, since it is 1/1500 of the diagonal. As long as the blur circles do not become larger than Z, they are below the resolution limit of the eye and the image is considered to be sharp. This creates the impression that the image not only has a plane of focus, but a focus area. A restricted depth of field is also problematic if the focus measurement is not carried out directly in the image plane, but with separate focusing disks or focus sensors , since focussing errors can easily occur due to tolerances in the image distance .

The following table shows the maximum size of the circles of confusion depending on the recording format of the respective camera :

Recording format	Image size	Aspect ratio	Screen diagonal	Z	Normal focal length
1/3 ″ digital camera sensor	4.4 mm x 3.3 mm	4: 3	5.5 mm	3.7 µm	6.4 mm
1 / 2.5 ″ digital camera sensor	5.3 mm x 4.0 mm	4: 3	6.6 mm	4.4 µm	7.6 mm
1 / 1.8 ″ digital camera sensor	7.3 mm x 5.5 mm	4: 3	9.1 mm	6.1 µm	10.5 mm
2/3 ″ digital camera sensor	8.8 mm x 6.6 mm	4: 3	11.0 mm	7.3 µm	12.7 mm
MFT sensor	17.3 mm x 13.0 mm	4: 3	21.6 mm	14.4 µm	24.9 mm
APS- C sensor	22.2 mm x 14.8 mm	3: 2	26.7 mm	17.8 µm	30.8 mm
APS-C sensor	23.7 mm x 15.7 mm	3: 2	28.4 mm	19.2 µm	32.8 mm
APS-H sensor	27.9 mm x 18.6 mm	3: 2	33.5 mm	22.4 µm	38.7 mm
35mm format	36 mm × 24 mm	3: 2	43.3 mm	28.8 µm	50.0 mm
Digital medium format	48 mm × 36 mm	4: 3	60.0 mm	40.0 µm	69.3 mm
Medium format 4.5 × 6	56 mm × 42 mm	4: 3	70.0 mm	46.7 µm	80.8 mm
Medium format 6 × 6	56 mm × 56 mm	1: 1	79.2 mm	52.8 µm	91.5 mm
Large formats	z. B. 120 mm x 90 mm	z. B. 4: 3	z. B. 150 mm	90-100 µm	z. B. 150 mm
Larger formats	up to 450 mm × 225 mm	-	-	> 100 µm	-

Calculate depth of field

Simple equation

The following variables are required:

• the lens focal length , for example 7.2 mm ${\displaystyle f}$
• the f-number indicates the ratio of the focal length to the diameter of the entrance pupil, for example 5.6. The entrance pupil is the virtual image of the physical diaphragm through the lens system in front of the object . If the diaphragm is in front of the entire lens system, it is also the entrance pupil. Below is replaced by in the formulas . While readings can be made directly from the camera's aperture ring, a value corrected by the pupil scale is: ${\displaystyle k'=f/D_{E}}$ ${\displaystyle D_{A}}$ ${\displaystyle f/k}$ ${\displaystyle k'}$ ${\displaystyle k}$ ${\displaystyle \beta =D_{A}/D_{E}}$ ${\displaystyle k=k'/\beta }$
• the object distance (distance of the focused object plane from the front principal plane), for example 1000 mm ${\displaystyle g}$
• the diameter of the circle of confusion , for example 0.006 mm. ${\displaystyle Z}$
• the distance of the image point of the object in the near or far point to the image plane of the setting range ${\displaystyle db}$

To approximate , the following formula can be used as the format diagonal of the recording format in mm and as the number of points to be distinguished along the diagonal: ${\displaystyle Z}$ ${\displaystyle d}$ ${\displaystyle N}$

${\displaystyle Z={\frac {d}{N}}\approx {\frac {d}{1500}}}$

This approximation is based on the assumption that the human eye can resolve a maximum of 1500 points over the image diagonal if the viewing distance is approximately equal to the image diagonal. For technical applications with higher image resolution, it may be necessary to select significantly higher. ${\displaystyle N}$

The lens equation

${\displaystyle {\frac {1}{b'}}+{\frac {1}{g'}}={\frac {1}{b+db}}+{\frac {1}{g'}}={\frac {1}{f}}}$

for the anterior hyperfocal plane and

${\displaystyle {\frac {1}{b'}}+{\frac {1}{g'}}={\frac {1}{b-db}}+{\frac {1}{g'}}={\frac {1}{f}}}$

for the posterior hyperfocal plane. In particular, the lens equation gives the relationship between image distance and object distance:

${\displaystyle b={\frac {f\cdot g}{g-f}}}$.

From geometrical considerations on the image widths, the circle of confusion and the diameter of the exit pupil

${\displaystyle {\frac {2\cdot (b\pm db)}{D_{A}}}={\frac {2\cdot b}{D_{A}\pm Z}}={\frac {2\cdot b}{{\frac {f}{k}}\pm Z}}={\frac {2\cdot db}{Z}}}$

you get:

${\displaystyle db={\frac {b\cdot k\cdot Z}{f\pm Z\cdot k}}={\frac {\frac {Z\cdot k\cdot f\cdot g}{g-f}}{f\pm Z\cdot k}}}$,

so that the solution for the object distance for the anterior or posterior hyperfocal point is: ${\displaystyle g^{\prime }}$

${\displaystyle g^{\prime }={\frac {f\cdot \left({\frac {f\cdot g}{g-f}}\pm {\frac {\frac {Z\cdot f\cdot g}{g-f}}{{\frac {f}{k}}\mp Z}}\right)}{\left({\frac {f\cdot g}{g-f}}\pm {\frac {\frac {Z\cdot f\cdot g}{g-f}}{{\frac {f}{k}}\mp Z}}\right)-f}}}$.

With the help of auxiliary variables , the equation can be solved to: ${\displaystyle a_{n}}$

${\displaystyle g^{\prime }={\frac {f\cdot a_{1}}{a_{1}-f}}}$

With

${\displaystyle a_{1}={\frac {f\cdot g}{g-f}}\pm {\frac {\frac {Z\cdot f\cdot g}{g-f}}{{\frac {f}{k}}\mp Z}}={\frac {f\cdot g}{f-g}}\pm {\frac {Z\cdot f\cdot g}{g-f}}\cdot {\frac {k}{f\mp Z\cdot k}}={\frac {f\cdot g}{g-f}}\cdot \left(1\pm {\frac {Z\cdot k}{f\mp Z\cdot k}}\right)={\frac {f\cdot g}{g-f}}\cdot a_{2}}$

${\displaystyle a_{2}=1\pm {\frac {Z\cdot k}{f\mp Z\cdot k}}={\frac {f\mp Z\cdot k\pm Z\cdot k}{f\mp Z\cdot k}}={\frac {f}{f\mp Z\cdot k}}}$

Now we get:

${\displaystyle {\frac {1}{a_{1}}}={\frac {(f\pm Z\cdot k)\cdot (g-f)}{f^{2}\cdot g}}={\frac {f\cdot g-f^{2}\pm Z\cdot k\cdot g-Z\cdot k\cdot f}{f^{2}\cdot g}}={\frac {f\cdot g}{f^{2}\cdot g}}-{\frac {f^{2}\pm Z\cdot k\cdot (g-f)}{f^{2}\cdot g}}={\frac {f\cdot g}{f^{2}\cdot g}}-a_{3}}$

With

${\displaystyle a_{3}={\frac {f^{2}\pm Z\cdot k\cdot (g-f)}{f^{2}\cdot g}}}$,

then we get for the far or near point of the depth of field:

${\displaystyle g^{\prime }={\frac {1}{1-f\cdot ({\frac {f\cdot g}{f^{2}\cdot g}}-a_{3})}}={\frac {f}{1-1+a_{3}\cdot f}}={\frac {f}{a_{3}\cdot f}}}$.

This results in:

${\displaystyle g^{\prime }={\frac {f^{2}\cdot g}{f^{2}\pm k\cdot Z\cdot (g-f)}}}$

In this way, for a given focal object distance, the front or rear hyperfocal object distance can be calculated with a given aperture and circle of confusion radius . ${\displaystyle g}$ ${\displaystyle g'}$ ${\displaystyle k}$ ${\displaystyle Z}$

The image scale for the rectilinear or gnomic projection is implicitly included in the initial geometrical considerations: where the angle of incidence of the light beam and R is the distance of the image point from the optical axis. Fisheye lenses work with other projections in order to achieve an opening angle of 180 °; this is not possible with rectilinear lenses. In principle, there are several projections that allow an opening angle of 180 ° or greater to achieve, a plurality of the fisheye lenses working with the projection equisoliden: . However, there are also lenses with equidistant ( ) and stereographic projection ( ). The latter type is very complex and therefore usually relatively expensive, but has the advantage that the typical distortions are more moderate. What all these lenses have in common, however, is that the derivation of the formula for the depth of field is not or only partially valid. A necessary condition is that the physical diaphragm is either behind the lens (diaphragm is the exit pupil) or that the part of the lens on the image side depicts the diaphragm gnomically. In addition, the basic assumption for the lens equation applies: due to the different projections, only approximately in the vicinity of the optical axis. Under no circumstances should the pupil scale be neglected. ${\displaystyle R=f\cdot \tan(\alpha )}$ ${\displaystyle \alpha }$ ${\displaystyle R=2\cdot f\cdot \sin(\alpha /2)}$ ${\displaystyle R=f\cdot \alpha }$ ${\displaystyle R=2\cdot f\cdot \tan(\alpha /2)}$ ${\displaystyle {\frac {B}{G}}={\frac {b-f}{f}}}$

The imaging scale for the gnomic projection shows that the derivative of the function , namely the angular resolution , is a function of the angle of incidence . Since the basic geometrical considerations were quite obviously formulated (the factor 2 indicates symmetry conditions) for circles of confusion in the optical axis, the question must be investigated whether the depth of field is a function of the angle of incidence. For any angle of incidence, the following relationship applies between the size of the circle of confusion and that of the exit pupil: ${\displaystyle R=f\cdot \tan(\alpha )}$ ${\displaystyle {dR \over d\alpha }={\frac {f}{\cos ^{2}(\alpha )}}}$ ${\displaystyle \alpha }$

${\displaystyle {\frac {Z}{db}}={\frac {{\frac {D_{A}}{2}}-B}{b-db}}+{\frac {{\frac {D_{A}}{2}}+B}{b-db}}={\frac {D_{A}}{b-db}}}$,

which in the end corresponds to the initial considerations. Thus the depth of field is independent of the angle of incidence.

Depth of field characteristics of a lens

Hyperfocal Distance

Different beam paths to determine the depth of field. It is focused on the hyperfocal distance. The far point is thus at infinity.

For the considerations that now follow, we must be clear that the object distance does not denote the distance of a real object from the main plane of the lens, but the adjustment distance on the lens for a fictitious object. however, it is always the distance from which the image distance results from the lens formula. ${\displaystyle g}$ ${\displaystyle g}$ ${\displaystyle b}$

From the formula for the far point of the depth of field:

${\displaystyle d_{f}={\frac {f^{2}\cdot g}{f^{2}-k\cdot Z\cdot (g-f)}}}$

one can see that if the condition is met, a singularity results. The adjustment range that fulfills this condition is called the hyperfocal distance: ${\displaystyle f^{2}=k\cdot Z\cdot (g-f)}$ ${\displaystyle g}$

${\displaystyle g=d_{h}={\frac {f^{2}}{k\cdot Z}}+f}$.

For the special case , the approximate formulas are: ${\displaystyle k\cdot Z\ll f}$

${\displaystyle d_{h}\approx {\frac {f^{2}}{k\cdot Z}}}$

The hyperfocal distance is the adjustment range that gives the largest depth of field.

Near point

Different beam paths to determine the depth of field. Focusing before hyperfocal removal. The far point is not at infinity.

For a given adjustment range , the distance from the main plane of the lens to the near point can be calculated as: ${\displaystyle g}$ ${\displaystyle d_{n}}$

${\displaystyle d_{n}={\frac {f^{2}\cdot g}{f^{2}+k\cdot Z\cdot (g-f)}}}$

From the condition for the singularity in the formula for the far point we know: ${\displaystyle d_{f}}$

${\displaystyle f^{2}=k\cdot Z\cdot (d_{h}-f)}$,

so that for a near point distance of: ${\displaystyle g=d_{h}}$

${\displaystyle d_{n}={\frac {f^{2}\cdot d_{h}}{2\cdot f^{2}}}={\frac {d_{h}}{2}}}$

results.

The near point is therefore at half the hyperfocal distance, and in this case objects from infinity to half the hyperfocal distance are imaged with sufficient focus. The general relationship between the near point and the setting range is obtained by adding the reciprocal values ​​of the near and far point:

${\displaystyle {\frac {1}{d_{n}}}+{\frac {1}{d_{f}}}={\frac {f^{2}+f^{2}}{f^{2}\cdot g}}={\frac {2}{g}}}$ .

For , which means that the adjustment range corresponds to the hyperfocal distance ( ), we again get half the adjustment range for the near point. ${\displaystyle 1/d_{f}=0}$ ${\displaystyle g=d_{h}}$

Depth of field

The distances of the near points and the distances of the far points with the associated depth of field (dark cyan) for different object distances ( blue) with a given hyperfocal distance (red) and a given focal length (violet). On the far right the focal plane F (violet) and in front of it the main plane of the optical image H (green). The image plane lies to the right of the focal plane and is not shown in the graphic. ${\displaystyle d_{n}}$ ${\displaystyle d_{f}}$ ${\displaystyle g}$ ${\displaystyle d_{h}}$ ${\displaystyle f}$

The depth of field extends from the near point to the far point with ${\displaystyle \Delta _{d}}$ ${\displaystyle d_{n}}$ ${\displaystyle d_{f}}$

${\displaystyle \Delta _{d}=d_{f}-d_{n}={\frac {2\cdot f^{2}\cdot g\cdot k\cdot Z\cdot (g-f)}{f^{4}-k^{2}\cdot Z^{2}\cdot (g-f)^{2}}}}$,

as long as the denominator takes positive values, which is equivalent to . ${\displaystyle g<d_{h}}$

If the set object distance is greater than or equal to the hyperfocal distance ( ), then the depth of field is infinite, since the far point is then at infinity. ${\displaystyle g\geq d_{h}}$

If the set object distance is equal to the focal length ( ), the depth of field is zero because the far point and the near point are identical. The image then lies in infinity. In macro shots with correspondingly large image scales, the result is usually very small depth of field areas. ${\displaystyle g=f}$

If one now wants to express the term by , then we get: ${\displaystyle k\cdot Z}$ ${\displaystyle d_{h}}$

${\displaystyle \Delta _{d}={\frac {2\cdot f^{2}\cdot g\cdot {\frac {f^{2}}{d_{h}-f}}\cdot (g-f)}{f^{4}-{\frac {f^{4}}{(d_{h}-f)^{2}}}\cdot (g-f)^{2}}}}$,

if . ${\displaystyle g<d_{h}}$

Approximations

If the focal length is neglected, i.e. with and , (the second condition always applies if the first is fulfilled because of ) the following approximate results for the depth of field range: ${\displaystyle g\gg f}$ ${\displaystyle d_{h}\gg f}$ ${\displaystyle g<d_{h}}$

${\displaystyle \Delta _{d}\approx {\frac {2\cdot f^{4}\cdot g^{2}}{d_{h}\cdot (f^{4}-{\frac {f^{4}\cdot g^{2}}{d_{h}^{2}}})}}={\frac {2}{{\frac {d_{h}}{g^{2}}}-{\frac {1}{d_{h}}}}},{\text{ wenn }}g<d_{h}}$

If the object distance is set to the Nth part of the hyperfocal distance, i.e. with

${\displaystyle g={\frac {d_{h}}{N}},{\text{ mit }}N>1}$,

then the depth of field decreases roughly proportionally to the square of : ${\displaystyle N}$

${\displaystyle \Delta _{d}\approx {\frac {2\cdot d_{h}}{N^{2}-1}}}$

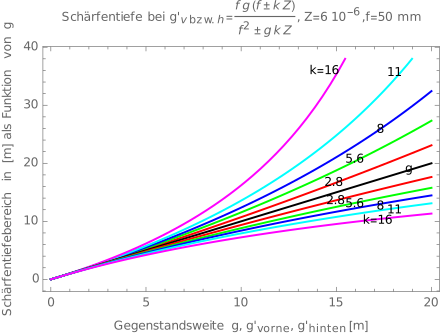
Dependencies

From the approximation formula for the hyperfocal distance it can easily be seen that this increases and the depth of field decreases when the focal length increases, the f-number becomes smaller (or the aperture larger) or the circle of confusion should be smaller. ${\displaystyle d_{h}}$ ${\displaystyle f}$ ${\displaystyle k}$ ${\displaystyle Z}$

Relationship between image angle , image distance and image diagonal ${\displaystyle \alpha }$ ${\displaystyle b}$ ${\displaystyle d}$

If you want to parameterize the hyperfocal distance according to the image diagonal, the assumption with regard to the crop factor is that the ratio between the focal length and the sensor diagonal is a constant as long as the opening angle of the image does not change. For a detailed consideration we start from the formula for the gnomic or rectilinear projection , which describes the relationship between the angle of incidence of the light and the distance of the image point from the optical axis. For an image circle with an opening angle (where the desired image angle is which is decisive for the perspective image effect) the relationship results: ${\displaystyle d_{h}}$ ${\displaystyle d}$ ${\displaystyle R=f\cdot \tan(\beta )}$ ${\displaystyle \alpha =2\cdot \beta }$ ${\displaystyle \alpha }$

${\displaystyle f={\frac {d}{2\cdot \tan \left({\frac {\alpha }{2}}\right)}},}$

Please note that when you focus on the image distance, the distance between the lens and the sensor changes, and thus also the opening angle of the image. An approach that assumes a relationship between b and d thus contradicts the initial requirements. Plugging this into the equation for hyperfocal distance gives: ${\displaystyle b\neq f}$

${\displaystyle d_{h}={\frac {d^{2}}{4\cdot k\cdot Z\cdot \tan ^{2}\left({\frac {\alpha }{2}}\right)}}+{\frac {d}{2\cdot \tan \left({\frac {\alpha }{2}}\right)}}=d\cdot ({\frac {N}{4\cdot k\cdot \tan ^{2}\left({\frac {\alpha }{2}}\right)}}+{\frac {1}{2\cdot \tan \left({\frac {\alpha }{2}}\right)}})}$

or for the approximation results: ${\displaystyle k\cdot Z\ll f}$

${\displaystyle d_{h}\approx {\frac {d\cdot N}{4\cdot k\cdot \tan ^{2}\left({\frac {\alpha }{2}}\right)}}}$

This means that the hyperfocal distance increases linearly with the image diagonal if the f-number , the number of image points on the image diagonal and the image angle are kept constant. It can also be seen from the formula that the smaller the f-number or the angle of view, the smaller the depth of field. All other things being equal, wide-angle lenses have a greater depth of field than telephoto lenses , or the hyperfocal distance is smaller with wide-angle lenses than with telephoto lenses. ${\displaystyle d_{h}}$ ${\displaystyle d}$ ${\displaystyle k}$ ${\displaystyle N}$ ${\displaystyle \alpha }$

Furthermore, it can be stated that the depth of field is always the same with a constant ratio of image sensor diagonal and f-number with the same image angle and the same number of acceptable circles of confusion. ${\displaystyle d}$ ${\displaystyle k}$

Example myopia

If the eye of a person with normal or farsightedness is focused on the hyperfocal distance, the area from half the hyperfocal distance to infinity is imaged and perceived sufficiently sharp. It is different with nearsighted people who, due to their nearsightedness, can only focus up to a maximum distance and the hyperfocal distance can therefore often not be reached.

For the calculation was a normal refractive power of the eye of 59 diopters accepted. This results in a normal focal length of 16.9 millimeters and an image circle diameter of 14.6 millimeters. Assuming the number of dots on the screen diagonal is 1500, then the diameter of the acceptable circle of confusion is 9.74 micrometers. With uncorrected nearsightedness, the eye can only focus on a maximum object distance, which results from the actual refractive power with the help of the imaging equation, which is usually specified as the negative diopter difference : ${\displaystyle \Phi _{\text{normal}}}$ ${\displaystyle f_{\text{normal}}={\frac {1}{\Phi _{\text{normal}}}}}$ ${\displaystyle d}$ ${\displaystyle N}$ ${\displaystyle Z}$ ${\displaystyle g}$ ${\displaystyle \Phi }$ ${\displaystyle \Delta \Phi }$

${\displaystyle \Phi =\Phi _{\text{normal}}-\Delta \Phi }$

${\displaystyle f={\frac {1}{\Phi }}}$

${\displaystyle g={\frac {1}{{\frac {1}{f}}-{\frac {1}{f_{\text{normal}}}}}}={\frac {1}{\Phi -\Phi _{\text{normal}}}}=-{\frac {1}{\Delta \Phi }}}$

The following table shows the depth of field areas for three different light situations and f-stop numbers for the eye as an example:

• F-number : wide pupil (diameter = 4.2 millimeters in dark surroundings) ${\displaystyle k=4}$
• F-number : middle pupil (diameter = 2.1 millimeters in the middle area) ${\displaystyle k=8}$
• F-number : small pupil (diameter = 1.1 millimeters in a bright environment) ${\displaystyle k=16}$

When the far point reaches infinity, the eye is focused on the hyperfocal distance and it is no longer necessary to focus even larger distances for sharp vision.

Ametropia in dpt ${\displaystyle \Delta \Phi }$		0	−0.25	−0.5	−0.75	−1	−1.5	−2	−3	−5	−10
Focal length in m ${\displaystyle f}$		0.0169	0.0169	0.0168	0.0167	0.0167	0.0165	0.0164	0.0161	0.0156	0.0145
	F-number ${\displaystyle k}$
Hyperfocal distance in m ${\displaystyle d_{h}}$	4th	7.39	7.33	7.27	7.21	7.15	7.03	6.91	6.69	6.28	5.41
Maximum object distance in m ${\displaystyle g}$	4th	7.39	4.00	2.00	1.33	1.00	0.67	0.50	0.33	0.20	0.100
Near point in m ${\displaystyle d_{n}}$	4th	3.70	2.59	1.57	1.13	0.88	0.61	0.47	0.32	0.19	0.098
Far point in m ${\displaystyle d_{f}}$	4th	∞	8.76	2.75	1.63	1.16	0.73	0.54	0.35	0.21	0.102
Depth of field in m ${\displaystyle \Delta _{d}}$	4th	∞	6.17	1.18	0.50	0.28	0.12	0.07	0.03	0.01	0.003
Hyperfocal distance in m ${\displaystyle d_{h}}$	8th	3.70	3.67	3.64	3.61	3.58	3.52	3.47	3.35	3.15	2.71
Maximum object distance in m ${\displaystyle g}$	8th	3.70	3.67	2.00	1.33	1.00	0.67	0.50	0.33	0.20	0.100
Near point in m ${\displaystyle d_{n}}$	8th	1.86	1.84	1.29	0.98	0.78	0.56	0.44	0.30	0.19	0.097
Far point in m ${\displaystyle d_{f}}$	8th	∞	∞	4.39	2.10	1.38	0.82	0.58	0.37	0.21	0.103
Depth of field in m ${\displaystyle \Delta _{d}}$	8th	∞	∞	3.10	1.12	0.59	0.25	0.14	0.06	0.02	0.006
Hyperfocal distance in m ${\displaystyle d_{h}}$	16	1.86	1.84	1.83	1.81	1.80	1.77	1.74	1.69	1.58	1.36
Maximum object distance in m ${\displaystyle g}$	16	1.86	1.84	1.83	1.33	1.00	0.67	0.50	0.33	0.20	0.100
Near point in m ${\displaystyle d_{n}}$	16	0.93	0.93	0.92	0.77	0.65	0.49	0.39	0.28	0.18	0.094
Far point in m ${\displaystyle d_{f}}$	16	∞	∞	∞	4.86	2.21	1.05	0.69	0.41	0.23	0.107
Depth of field in m ${\displaystyle \Delta _{d}}$	16	∞	∞	∞	4.09	1.56	0.57	0.30	0.13	0.05	0.013

Wave optical depth of field

All optical images are limited by diffraction , so that a single point can never be mapped onto a point, but only onto a diffraction disk (or Airy disk ). The sharpness of separation between two neighboring diffraction disks defines a maximum permissible circle of confusion, analogous to photographic film. According to the Rayleigh criterion , the intensity between two neighboring pixels must drop by 20 percent in order to be considered sharp. The size of the diffraction disk depends on the wavelength of the light. Rayleigh's depth of field is defined as the area within which the image size does not change, i.e. constantly corresponds to the smallest possible (i.e. diffraction-limited) value:

${\displaystyle d_{R}={\frac {\lambda }{2\,n\sin ^{2}u}}}$

Here is the wavelength , n the refractive index and u the aperture angle of the imaging system. ${\displaystyle \lambda }$

Rayleigh's depth of field is relevant in diffraction-limited optical systems, for example in microscopy or photolithography . In photography, a wave-optical blurring beyond the beneficial aperture makes itself felt in the image. ${\displaystyle {k_{f}}}$

${\displaystyle k_{f}={\frac {Z}{1{,}22\,\lambda \,(\beta +1)}}}$

Here is the maximum permissible circle of confusion, the image scale and the wavelength . ${\displaystyle Z}$ ${\displaystyle \beta }$ ${\displaystyle \lambda }$

For common applications (small image scale) in 35mm photography, a useful aperture of over f / 32 results , so that diffraction hardly plays a role except in macro photography .

Since the small sensors of modern compact digital cameras require very small permissible circles of confusion, the range of the usual f-stops is moving . For a 1 / 1.8 ″ sensor, for example, the useful aperture is around f / 8, and even less at close range. ${\displaystyle k_{f}}$

Pinhole camera

In a pinhole camera the size depends of the circles of confusion from the object distance g , the image distance b and the hole diameter D from. An object is shown sufficiently sharp if:

${\displaystyle D+{\frac {D\cdot b}{g}}\leqq Z}$

The far point of a pinhole camera is always at infinity. For very large object distances g the condition simplifies to: . This means that the hole diameter must not be larger than the permissible diameter of the circle of confusion, otherwise a sufficiently sharp image is no longer possible with a pinhole camera even in the far range. ${\displaystyle d_{f}}$ ${\displaystyle D\leqq Z}$

Application in photography

Lenin portrait, 1920

By using a smaller aperture, the circle of confusion is reduced

Aperture 22 - The area in focus extends from front to back.

Aperture 10 - The sharp area is in the middle, the transitions to the unsharp areas are clearly visible.

Aperture 2 - The sharply displayed area is now only limited to the daisies in the center of the image. The near and far point are close together.

Manual zoom lenses . The aperture curves show how the depth of field decreases with increasing focal length . On the left lens with a focal length of 28 mm, aperture 22 and focusing at 1.2 m, a range from 0.6 m to infinitely sharp is shown. On the right lens, with a focal length of 80 mm, aperture 22 and focusing at 10 m, a range from 5 m to infinitely sharp is shown.

Disc calculator for determining iris, focus and depth of field for the right in the left image displayed 80-200mm Zoom Lens, for example, the focal lengths 80, 90, 105, 120, 135, 150, 170 and 200 mm.

Reduction of the depth of field after the Brenizer method. Left normal shot, right stitching from five photos with an f4 / 250mm lens

Image composition with depth of field

The targeted use of the depth of field by setting the f-number , the distance and the focal length enables the viewer to focus on the main subject. To do this, the photographer restricts the depth of field as closely as possible around the plane on which the main subject is located. This causes the foreground and background to be out of focus. This selective blurring is less of a distraction from the main subject, which is accentuated by the selective focus .

A restricted depth of field can lead to so-called ghost spots in the recording in photographic recordings with point-like objects that are located somewhat outside the object range in focus .

For small recording formats, e.g. B. When creating enlarged sections or when using digital cameras with small image sensors ( format factor ), the maximum permissible circle of confusion is reduced (with the same number of pixels ), which initially reduces the depth of field. The smaller recording formats, however, require proportionally smaller lens focal lengths in order to guarantee constant viewing angles - this, on the other hand, increases the depth of field. Both the reduction in size of the image sensors (⇒ reduction of the maximum permitted circles of confusion) and the reduction in the focal length of the lens, which is therefore necessary, affect the depth of field. The influences are in opposite directions, but they do not balance each other out. The maximum permissible circle of confusion is linear and the lens focal length is approximately quadratically included in the depth of field - so the influence of the lens focal length predominates. As a result, the depth of field is correspondingly larger and it is becoming increasingly difficult to use selective sharpness as a photographic design element directly when taking photos . In order for both influences to balance each other out, the pixel density of the sensors would have to grow approximately quadratically with the reduction in the sensor dimensions, which quickly leads to technical limits.

Factors influencing the depth of field

Influence of aperture on exposure and depth of field

The focus area can be influenced by several factors (see section Calculating the depth of field ):

• It is expanded by stopping down the aperture and narrowed by stopping it down. The smaller the aperture, the larger the focus area.
• Another factor influencing the depth of field is the image scale . The reproduction scale depends on the focal length of the lens and the object distance ( is the image distance ). ${\displaystyle \beta }$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle b}$

${\displaystyle \beta ={\frac {b}{g}}={\frac {f}{g-f}}}$

The smaller the image scale, the greater the depth of field. A wide-angle lens with a shorter focal length produces a greater depth of field than a telephoto lens with a long focal length for the same object distance.

• For camera systems with different image diagonals and thus correspondingly different normal focal lengths , assuming otherwise the same conditions ( f-number , image angle and image resolution ), the greater the image diagonal, the smaller the depth of field. With larger cameras with a given f-number, it is therefore easier to limit the depth of field (e.g. when taking portraits with a blurred background) than with small cameras. If a subject is recorded once in such a way that it completely fills the sensor height on the sensor, and once in such a way that it has a height that is a factor of less on the sensor by simply increasing the distance to the subject, the depth of field increases below roughly square with . Example: Reducing the image height by a factor of approximately four times the depth of field. This rule of thumb applies if the distance to the subject is less than about a quarter of the hyperfocal distance. This rule of thumb applies accordingly to different sensor sizes: Reducing the sensor height by the factor increases the depth of field by approximately the factor if the subject fills the sensor height in both cases and the same aperture is set in both cases. The focal length has no significant influence, see below. ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x=2}$ ${\displaystyle x}$ ${\displaystyle x^{2}}$
• The rather academic comparison of different camera systems with different image diagonals looks different if one does not compare lenses with the same f-number , but with lenses with the same entrance pupil , i.e. lenses that project the same light beam emanating from an object point onto an image point. The proportionality between the sensor diagonal and the focal length: has already been shown. As long as the approximation applies, the following results for the hyperfocal distance:, where is the pupil scale. This means that two objectives with the same entrance pupil and the same angle of view produce the same depth of field regardless of the sensor size, as long as the pupil scale is identical. This consideration is academic insofar as it is rarely used for zoom lenses, since the pupil scale usually changes when the lens groups are shifted relative to one another and, on the other hand, it is difficult to find two lenses that meet the conditions. ${\displaystyle d\propto f}$ ${\displaystyle k\cdot Z\ll f}$ ${\displaystyle d_{h}\propto D_{E}\cdot \beta }$ ${\displaystyle \beta =D_{A}/D_{E}}$

• The distribution of the depth of field in front of and behind the focused object varies with the set distance: a ratio of approximately 1: 1 is achieved in the close close range, with increasing distance the proportion behind the focused object increases continuously, the latter extremely if the infinity setting is still just is placed in the focus area (= hyperfocal distance ).
• The depth of field practically does not change in certain areas if a subject is imaged once with a short focal length from a short distance and once with a long focal length from a greater distance so that it has the same size in the image. The aforementioned influence of the focal length is compensated for by the other object distance. This rule applies if the same aperture is used in both cases and if the distance to the subject with the short focal length is less than about a quarter of the hyperfocal distance.
• Using the focus stacking method , an apparently extremely large depth of field can be achieved by taking a series of images with various distance settings and then reassembling the results using computer graphics methods.
• Conversely, the Brenizer method named after the American photographer Ryan Brenizer , who perfected and popularized this process, can be used to produce wide-angle or panorama photographs with a very shallow depth of field. Here, images made with a bright telephoto lens with a small area of ​​focus are combined to a photo with a large angle of view by means of stitching .

Camera settings

In the macro range, the depth of field s is defined solely by the image scale, the aperture set and the permitted blur circle diameter . It is completely independent of the focal length (as long as the permitted circle of uncertainty is significantly smaller than the focal length).

It is calculated as follows:

${\displaystyle {\text{Verkleinerungsfaktor}}=1/{\text{Abbildungsmassstab}}}$

${\displaystyle v={\text{Verkleinerungsfaktor}}^{2}+{\text{ Verkleinerungsfaktor}}}$

${\displaystyle s=2\cdot {\text{Unschärfekreisdurchmesser}}\cdot {\text{Blendenzahl}}\cdot v}$

In the non-macro area (the error exceeds 10%: reduction factor> 0.3 focal length / blur circle radius / f-number) the formula must be expanded to include the correction value : ${\displaystyle 1-w^{2}}$

${\displaystyle v={\text{Verkleinerungsfaktor}}^{2}+{\text{Verkleinerungsfaktor}}}$

${\displaystyle w={\text{Unschärfekreisradius}}\cdot {\text{Blendenzahl}}\cdot {\text{Verkleinerungsfaktor}}/{\text{Brennweite}}}$

${\displaystyle s=2\cdot {\text{Unschärfekreisdurchmesser}}\cdot {\text{Blendenzahl}}\cdot v/(1-w^{2})}$

The scope of this formula ends when negative values ​​are obtained. Then the far point is at infinity, the depth of field is then infinitely large, the far point is behind the lens, concave wave fronts are within the focus area.

For practical use in the field:

• you remember for your current camera (with many crop DSLRs around 0.4 mm) ${\displaystyle 2\cdot 10\cdot {\text{Unschärfekreisdurchmesser}}}$
• For a reduction factor of 10, 5, 2, 1 you have to multiply this value by 110, 30, 5 or 2 (and get 44 mm, 12 mm, 2 mm or 0.8 mm).
• This gives the depth of field for the f-number 10. For other f-numbers, this value increases or decreases proportionally.

Nikon tilt-shift lens

Scheimpflug shot in the large format camera

Further remarks:

• Some electronically controlled cameras offer the option of first marking the front and then the rear point of the desired focus area with the shutter release (DEP function). The camera then calculates the aperture required for this and adjusts the focus so that the sharpness corresponds exactly to the marked area. The A-DEP function of current digital cameras has nothing to do with this, however, here the camera determines the front and rear focus point by using all AF fields.
• The adjustment options of view cameras allow the use of the so-called Scheimpflug setting . This does not change the focus area of ​​the lens, but allows the focus level to be shifted and thus adapted to the subject. For small and medium format cameras there are special tilt or swing bellows devices or so-called tilt lenses for the same purpose, a function that is often combined with a shift function for possible parallel displacement of the plane of focus.
• Some special lenses have the function of variable object field curvature ( VFC , variable field curvature), which allows the continuous convex or concave deflection of the plane of focus in a rotationally symmetrical manner.
• With a special disk calculator , depth of field calculations can be carried out for a given lens while on the move. With a given aperture, the optimal focus point for a desired depth of field range or the resulting depth of field range for a given focus point can be determined. In addition, the aperture required to achieve a desired depth of field can be determined.

Applications in computer graphics

For reasons of speed, many known methods in computer graphics use direct transformations (e.g. via matrix multiplications ) in order to convert the geometry into image data. However, these mathematical constructs also result in an infinite depth of field. However, since depth of field is also used as a design tool, various methods have been developed to mimic this effect.

The direct rendering of polygons has established itself in 3D computer games . This method has speed advantages over indirect rendering ( ray tracing ), but it also has technical limitations. The depth of field cannot be calculated directly, but has to be approximated in a post- processing step using a suitable filter. These are selective blurs that use the Z-buffer for edge detection. This prevents objects further in front from being included in the filtering of the background when the image is blurred and vice versa. Problems arise in particular with transparent objects, since these have to be treated in separate post-processing steps, which has a negative effect on the speed of the image build-up.

Rendering of a magnifying glass with infinite depth of field

The same graphic with finite depth of field and focus on the magnified text

With indirect rendering, both the method described above and multisampling can be used, whereby a large number of samples are required to create a depth of field effect. Therefore, these methods are preferably used in renderers that are unbiased . These correspond to a method based very closely on the model of a camera, where individual photons / rays and their color value are accumulated on a film, i.e. In other words, as the calculation continues and the number of samples increases, the image noise is reduced further and further. In contrast to the first method, it produces more believable and realistic results ( bokeh etc.), but is also orders of magnitude slower, which is why it is not yet suitable for real-time graphics .

The images in this section were calculated using an unbiased renderer. For sufficient noise suppression, 2500 samples per pixel were necessary, which corresponds to a tracking of approx. 11.6 billion beam paths, which were followed including multiple reflections and refractions in the scene.

See also

• 35 millimeter adapter (depth of field for conventional video cameras)
• Deep focus cinematography (the greatest possible depth of field in the film)
• Bokeh (appearance in the blurred distance range)
• Diffraction blur if the aperture is too small (closed)

literature

• Heinz Haferkorn: Optics. Physical-technical basics and applications . Verlag Harri Deutsch, Frankfurt / Main 1981, ISBN 3-87144-570-3 , chap. 6.4.3, pp. 562-573
• Andreas Feininger : Andreas Feininger's Great Photo Teaching . New edition Heyne Verlag Munich 2001, ISBN 3-453-17975-7

Web links

Commons : depth of field  - collection of images

• Depth of field calculator download
• Depth-circular slide video tutorial
• Depth of field in photographic practice
• Depth of field , calculation methods and formulas in the Wikibook Digital imaging processes
• Depth of field, image scale and close-up lens calculator (German). Considered u. a. also diffraction and auxiliary lenses. Can output individual depth of field tables. A bit more complicated to use for digital cameras.
• Comparison of different f-numbers and their depth of field in images
• Background blur calculator (English)
• dofmaster Calculation of the depth of field for different cameras and focal lengths depending on the aperture. Free software for creating depth of field calculators.

Individual evidence

1. ↑ The photographer Emil Otto Hoppé was one of the first to use the shortcoming of very shallow depth of field as an aesthetic stylistic device. In his self-portrait from 1926 ( picture below ( memento of the original from July 19, 2011 in the Internet Archive ) Info: The archive link has been inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this note. ) Are only a small part of his hand and his eyes were sharp - Hoppé loved hands.