Equidistance (geometry)

Vertical lines, bisectors and parabolas as equidistant curves

Ellipse and hyperbola as equidistance curves

Equidistance curves of two Bezier curves

In geometry, equidistance refers to the property of points (of the plane or space) that are equidistant from two specified geometric objects such as points, curves or surfaces.

The following applies:

(PP) The distance from a point to a point is the Euclidean distance . ${\displaystyle P:{\vec {p}}}$ ${\displaystyle Q:{\vec {q}}}$ ${\displaystyle d(P,Q)=|{\vec {p}}-{\vec {q}}|}$

(PC) The distance from a point ${\displaystyle d(P,c)}$ to a curve is the shortest Euclidean distance from points on the curve . In the case of smooth curves , this is the length of the shortest perpendicular to the curve or the distance to an edge point. ${\displaystyle P}$ ${\displaystyle c}$ ${\displaystyle P}$ ${\displaystyle c}$ ${\displaystyle P}$

The distance to a surface is defined in the same way.

Examples:
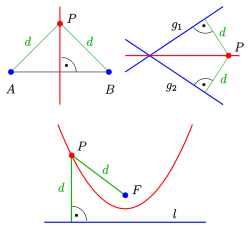
a) Every point of the perpendicular of a line has the same distance to the two end points of the line.
b) Every point of the bisector of two intersecting straight lines has the same distance to the two straight lines.
c) Every point of a parabola has the same distance to the focal point and the line.
d) Every point of an ellipse has the same distance to a focal point and to a guide circle.
e) Every point of a hyperbola has the same distance to a focal point and to a guide circle.

In the English literature, equidistance curves / surfaces are referred to as bisector curves / surfaces .

Equidistance curves and surfaces should not be confused with parallel curves / surfaces. In the latter, all points have the same distance from a curve / surface.

Mathematical description

The closest description of an equidistance curve uses the distance function . In the above examples, the distance function is simple:
1) distance between two points in : . 2) Distance of a point from a straight line: s. HESSE normal form . 3) distance of a point of a circle with the center and radius : . ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle d={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}}$

${\displaystyle (x,y)}$ ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle r}$ ${\displaystyle d=|{\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}-r|}$

In all other cases, it is not possible to give a simple description of the distance function and thus the equidistance curves / surfaces. In the literature, special cases are examined in which the equidistance curves can at least be described by rational functions. If one is dependent on numerical methods, it is easiest to describe an equidistance curve as an implicit curve or implicit surface with the help of distance functions. If necessary, oriented distance functions are used that differentiate the sides of a curve (in the plane) or surface with the help of the sign.

Example: Let it be the distance functions of two Bézier curves . One point on the associated equidistance curve then satisfies the equation . So is ${\displaystyle d(x,y;c_{1}),d(x,y;c_{2})}$ ${\displaystyle c_{1},c_{2}}$ ${\displaystyle (x,y)}$ ${\displaystyle d(x,y;c_{1})=d(x,y;c_{2})}$

• ${\displaystyle d(x,y;c_{1})-d(x,y;c_{2})=0}$

an implicit representation of the equidistance curve. In order to be able to calculate points of this implicit curve, one must be able to evaluate the distance functions numerically. Suitable algorithms for this are made available in the literature.

Equidistant surfaces are also described in space in an analogous manner . The objects involved can be points as well as curves and surfaces.

Equidistant surfaces to 1) two crooked straight lines (left) and 2) a straight line and a helix

Equidistant surface to a Bezier curve and a Bezier surface

Examples in space:
1) For the crooked straight line , the implicit representation of the equidistance area results initially . After removing the roots, the area can be expressed by the equation ${\displaystyle g_{1}:y^{2}+z^{2}=0,\ g_{2}:x^{2}+(z-1)^{2}=0}$ ${\displaystyle {\sqrt {y^{2}+z^{2}}}-{\sqrt {x^{2}+(z-1)^{2}}}=0}$

${\displaystyle z=(x^{2}-y^{2}+1)/2}$

describe. So it is a hyperbolic paraboloid (see picture).
2) The next picture shows the equidistant surface to the straight line and the helix ( helix ) . 3) The last picture shows the equidistant surface to a Bezier curve and a Bezier surface. ${\displaystyle x^{2}+y^{2}=0}$ ${\displaystyle (\cos t,\sin t,0.5t)}$

literature

1. ^ M. Peternell: Geometric Properties of Bisector Surfaces , Graphical Models 62, 202-236 (2000)
2. ↑ G. Elber, Myung-Soo Kim: Bisector Curves of Planar Rational Curves http://www.cs.technion.ac.il/~gershon/papers/bisect2d.pdf
3. ↑ G. Elber, MS Kim: The Bisector surfaces of rational space curves , ACM Trans Graph 17, p. 32-49
4. ^ E. Hartmann: The normal form of a space curve and its application to surface design , The Visual Computer 2001, pp 445-456
5. ↑ G. Elber, MS Kim: A computational model for nonrational bisector surfaces: curve-surface and surface-surface bisector surfaces , Proceedings of Geometric Modeling and Processing 2000, Hongkong, IEEE, pp 364-372
6. ↑ Gerald Farin: Curves and Surfaces for CAGD. A practical guide. 5th ed. Academic Press, San Diego 2002, ISBN 1-55860-737-4 , p. 252

Web links

• E. Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN , pp. 45, 62