Parallel curve

In mathematics, a parallel curve is a generalization of the concept of a parallel to a given straight line in the Euclidean plane. There are essentially two ways of defining it:
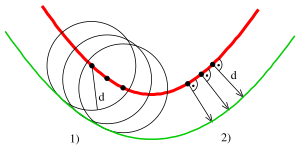
- 1st possibility: The parallel curve of a curve at distance d is the envelope of the circles with radius d and center points on the curve .
- 2nd possibility: The parallel curve of a curve consists of the points of the plane which lie on the normal of a point at a distance d.
The two definitions are equivalent for smooth curves in a (possibly small) neighborhood. The first option has the advantage of drawing approximately parallel curves by hand using a compass and a curve ruler . The second option has the advantage of drawing the curve with a simple computer program and calculating geometric details (tangent and curvature).
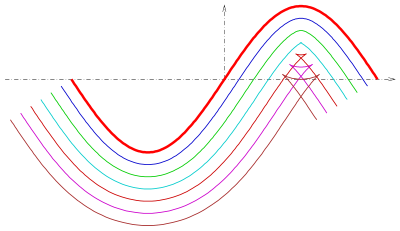
A parallel curve of a curve is only in the simple cases of a straight line or a circle a curve of the same type (straight line or circle). In general, a parallel curve has a much more complicated analytical description than the given curve (see below). If d is chosen too large, a parallel curve can contain singularities (peaks) even with a simple smooth curve (see figure). This happens when d is equal to the radius of the curvature of a curve point, i.e. H. when the parallel curve touches the evolute of the given curve (see 4th picture).
Note that a parallel curve is only created in the case of a straight line by shifting the given curve. With a circle, a parallel curve is created by stretching it at the center. In general, there is no such simple relationship between curve and parallel curve.
Parallel curves are of great importance in CAD , especially in CAM ( computer-aided manufacturing ). Parallel curves are used to mill workpieces with specified contours. The axis of a cylindrical milling head moves there on a parallel curve of the contour of the workpiece.
In the CAD area, parallel curves are mostly called offset curves . The equidistant function is offered by most CAD systems. For example, in AUTOCAD, the German command is “relocate”. With this you can, for example, very quickly define a drainage with a specified distance around a house.
The 1st definition of a parallel curve (envelope of circles) plays a practical role in descriptive geometry for determining the outline of a pipe surface and for the slope of a horizontal curve.
In a rotary engine , the envelope curve of the trochoid (wheel curve) of the rotor at distance d is an equidistant.
The concept of parallel curves can also be applied to surfaces in Euclidean space. These surfaces are then called parallel surfaces or offset surfaces and are the envelopes of a 2-parametric set of spheres . A pipe surface can be understood as an object in between . It is the envelope of a 1-parametric set of spheres, i.e. H. the centers of the spheres lie on a curve (in space). More generally, higher-dimensional parallel surfaces are referred to as equidistant hypersurfaces .
Parallel curve of a parameterized curve
If there is a regular parametric representation of the given curve , the above 2nd possibility of definition provides the following parametric representation of the parallel curve at a distance :
- with the unit normal .
In coordinates results
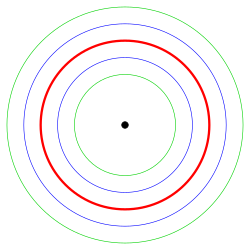
The distance parameter can also be negative. Then you get a parallel curve at a distance on the other side of the curve (see picture of a circle with parallel curves on both sides). It is easy to check that in the case of a straight line (circle) the parallel curve is again a straight line (circle).
Geometric properties:
- , d. H. the tangent vectors are parallel for the same parameter.
- , where the curvature of the given curve and the curvature of the parallel curve for the parameter t.
For a polynomial curve (i.e. and are polynomials) the parallel curves are i. a. no more polynomial curves. This is uncomfortable in the CAD area, since most CAD systems can only process polynomial or perhaps rational curves. In order to obtain at least rational parallel curves, the root in the definition of a parallel curve must be extractable, i.e. H. be a polynomial again. Such curves are called pythagorean hodograph curves and were mainly investigated by RT FAROUKI.
Parallel curve of an implicit curve
The analytical description of a parallel curve of an implicit curve is usually not possible. Parallel curves can only be described implicitly in the simple straight line and circle cases, since the distance of a point from the curve can easily be specified in these cases: E.g .:
- Straight line → distance function: (Hesse normal form)
- District → distance function: .
In the general case, an oriented distance function can be demonstrated under certain conditions , but this must then be evaluated numerically. In any case:
- The parallel curve to the distance d is the level line of the associated distance function .
Properties of the distance function:
- ,
- ,
- .
Example:
The last picture shows parallel curves of the implicit curve . Note: the curves are not parallel curves , because in the area in question is not fulfilled everywhere.
Examples
Involute
The involutes of a curve form a family of parallel curves. For example, the involute circles form a family of parallel spirals (see picture).
Parabola with envelope curve of a set of circles
Black: function graph of .
Red: One inner and one outer equidistant with a distance of 0.25 from the function graph.
Violet: circles centered on the function graph and radius 0.25. The equidistant is the envelope of the host of all such circles.
Light blue: Distance in the direction of the normal field of the function graph, the end points are 0.25 apart from the function graph, the set of all these end points forms the equidistant.
Brown: tangent array at the lower equidistant.
See also
Individual evidence
- ^ A b E. Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. P. 30.
- ↑ Rida T. Farouki: Pythagorean hodograph Curves: Algebra and Geometry Inseparable (Geometry and Computing). Springer, 2008, ISBN 978-3-540-73397-3 .
- ^ E. Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. P. 81, p. 30, 41, 44.
literature
- RT Farouki, CA Neff: Analytic properties of plane offset curves. In: CAGD. 7: 83-99 (1990).
- Josef Hoschek: Offset curves in the plane. In: CAD. 17, pp. 77-81 (1985).
- Takashi Maekawa: An overview of offset curves and surfaces. In: CAD. 31 (1999), pp. 165-173.