Heyting algebra

In mathematics are Heyting algebras special partial orders ; at the same time the concept of Heyting algebra is a generalization of the concept of Boolean algebra . Heyting algebras emerge as models of intuitionistic logic , a logic in which the principle of the excluded third party generally does not apply. Complete Heyting algebras are a central subject of point-free topology .

Heyting algebra is named after Arend Heyting .

Formal definition

A Heyting algebra is a bounded association with the property that it is for all and in a largest element in with ${\displaystyle H}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle H}$ ${\displaystyle x}$ ${\displaystyle H}$

${\displaystyle a\wedge x\leq b.}$

This element is the relative Pseudokomplement of respect called and written. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a\rightarrow b}$

An equivalent definition can be given using the following figures:

${\displaystyle f_{a}\colon H\rightarrow H}$ defined as ${\displaystyle f_{a}(x)=a\wedge x,}$

for solid in . A bounded lattice is a Heyting algebra if and only if all mappings are left adjoints of a Galois connection . In this case the respective right adjoint is given by , where it is defined as above. ${\displaystyle a}$ ${\displaystyle H}$ ${\displaystyle H}$ ${\displaystyle f_{a}}$ ${\displaystyle g_{a}}$ ${\displaystyle g_{a}(x)=(a\rightarrow x)}$ ${\displaystyle \rightarrow }$

A complete Heyting algebra is a Heyting algebra that is a complete lattice .

In every Heyting algebra one can define the pseudo complement of an element by , where 0 is the smallest element of the Heyting algebra. It applies , and besides, is the greatest element with this property. However, it is generally not true that it is only a pseudo complement and not a real complement . ${\displaystyle \lnot x}$ ${\displaystyle x}$ ${\displaystyle \lnot x=(x\rightarrow 0)}$ ${\displaystyle a\wedge \lnot a=0}$ ${\displaystyle \lnot a}$ ${\displaystyle a\vee \lnot a=1}$ ${\displaystyle \lnot }$

Examples

The free Heyting algebra over a generator (Rieger – Nishimura Association)

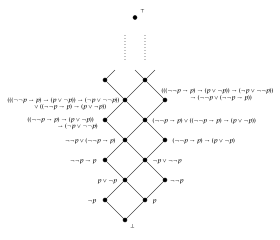
• Every total order that is a bounded lattice is also a Heyting algebra with ${\displaystyle (a\to b)={\begin{cases}1&a\leq b\\b&{\text{sonst.}}\end{cases}}}$

• Every Boolean algebra is a Heyting algebra, with defined as . ${\displaystyle a\to b}$ ${\displaystyle \lnot a\lor b}$

• The simplest Heyting algebra, which is not already a Boolean algebra, is the linearly ordered set {0, ½, 1} with the following operations:

${\displaystyle a\land b}$ ${\displaystyle b}$ ${\displaystyle a}$ 0 ½ 1 0 0 0 0 ½ 0 ½ ½ 1 0 ½ 1

${\displaystyle a\lor b}$ ${\displaystyle b}$ ${\displaystyle a}$ 0 ½ 1 0 0 ½ 1 ½ ½ ½ 1 1 1 1 1

${\displaystyle a\rightarrow b}$ ${\displaystyle b}$ ${\displaystyle a}$ 0 ½ 1 0 1 1 1 ½ 0 1 1 1 0 ½ 1

${\displaystyle a}$ ${\displaystyle \neg a}$ 0 1 ½ 0 1 0

You can see that violates the proposition of the excluded third party. ${\displaystyle {\tfrac {1}{2}}\lor \neg {\tfrac {1}{2}}={\tfrac {1}{2}}\lor 0={\tfrac {1}{2}}}$

• The lattice of the open sets of a topological space is a complete Heyting algebra. In this case the interior is the union of and , where denotes the complement of the open set . Not all complete Heyting algebras can be generated in this way. Related questions are examined in point-free topology , in which complete Heyting algebras are also called frames or locales . ${\displaystyle A\rightarrow B}$ ${\displaystyle A_{c}}$ ${\displaystyle B}$ ${\displaystyle A_{c}}$ ${\displaystyle A}$

• The Lindenbaum algebra of intuitionist propositional logic is a Heyting algebra. It is defined as the set of all propositional formulas, ordered by the logical consequence relation: for two formulas and be if and only if . However, there is only a quasi-order that induces a partial order, which is then the desired Heyting algebra. ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle F\leq G}$ ${\displaystyle F\models G}$ ${\displaystyle \leq }$

• The global elements of the sub-object classifier of an elementary topos form a Heyting algebra; it is the Heyting algebra of the truth values ​​of the higher-order intuitionistic logic induced by the topos. ${\displaystyle \Omega }$

properties

Heyting algebras are always distributive ; H.

1. ${\displaystyle x\land (y\lor z)=(x\land y)\lor (x\land z)}$ and
2. ${\displaystyle x\lor (y\land z)=(x\lor y)\land (x\lor z)}$.

Distributivity is sometimes postulated as an axiom, but it already follows from the existence of relative pseudocomplements. The reason for the validity of 1) is that as the lower adjoint of a Galois connection preserves all existing suprema . 1) is nothing more than the preservation of binary suprema through . ${\displaystyle x\wedge -}$ ${\displaystyle x\wedge -}$

With a similar argument the following infinitary distributive law can be shown in complete Heyting algebras:

${\displaystyle x\wedge \bigvee Y=\bigvee \{\,x\wedge y\mid y\in Y\,\}}$

for all out and subsets of . ${\displaystyle x}$ ${\displaystyle H}$ ${\displaystyle Y}$ ${\displaystyle H}$

A lattice with a binary operation is a Heyting algebra if and only if: ${\displaystyle A}$ ${\displaystyle \rightarrow }$

1. ${\displaystyle (a\rightarrow a)=1}$,
2. ${\displaystyle a\wedge (a\rightarrow b)=a\wedge b}$,
3. ${\displaystyle b\wedge (a\rightarrow b)=b}$,
4. ${\displaystyle a\rightarrow (b\wedge c)=(a\rightarrow b)\wedge (a\rightarrow c)}$.

Not every Heyting algebra obeys De Morgan's two laws . However, the following statements about any Heyting algebra are equivalent: ${\displaystyle H}$

1. ${\displaystyle H}$ fulfills both of De Morgan's laws.
2. ${\displaystyle \lnot (x\wedge y)=\lnot x\vee \lnot y}$, for everyone . ${\displaystyle x,y\in H}$
3. ${\displaystyle \lnot x\vee \lnot \lnot x=1}$, for everyone . ${\displaystyle x\in H}$
4. ${\displaystyle \lnot \lnot (x\vee y)=\lnot \lnot x\vee \lnot \lnot y}$, for everyone . ${\displaystyle x,y\in H}$

The pseudo complement of an element of is the supremum of the set , and it belongs to that set (i.e. it holds ). ${\displaystyle x}$ ${\displaystyle H}$ ${\displaystyle \{\,y\mid y\wedge x=0\,\}}$ ${\displaystyle x\wedge \lnot x=0}$

An element of a Heyting algebra is called regular if one of the following equivalent conditions holds: ${\displaystyle x}$ ${\displaystyle H}$

1. ${\displaystyle x=\lnot \lnot x}$.
2. ${\displaystyle x=\lnot y}$for one off . ${\displaystyle y}$ ${\displaystyle H}$

A Heyting algebra is a Boolean algebra if and only if one of the following equivalent conditions holds: ${\displaystyle H}$

1. Every out is regular. ${\displaystyle x}$ ${\displaystyle H}$
2. ${\displaystyle x\vee \lnot x=1}$for all of . ${\displaystyle x}$ ${\displaystyle H}$

In this case the element is the same . ${\displaystyle a\rightarrow b}$ ${\displaystyle \lnot a\vee b}$

In every Heyting algebra, the smallest and largest elements, 0 and 1, are regular.

The regular elements of a Heyting algebra form a Boolean algebra. If not all elements of Heyting's algebra are regular, then this Boolean algebra is not a subdivision of Heyting's algebra because the supremums operations are different.

If there is a Heyting algebra, it may be that the associated dual association is also a Heyting algebra. If so, it can be an element in forming the Pseudokomplement and this as an element of conceive. It always applies then . In general, the inequality does not hold in the other direction: is equivalent to and to . ${\displaystyle H}$ ${\displaystyle H^{\text{op}}}$ ${\displaystyle a\in H}$ ${\displaystyle H^{\text{op}}}$ ${\displaystyle {\bar {a}}}$ ${\displaystyle H}$ ${\displaystyle \lnot a\leq {\bar {a}}}$ ${\displaystyle {\bar {a}}\leq \lnot a}$ ${\displaystyle a\lor \lnot a=1}$ ${\displaystyle a\land {\bar {a}}=0}$

In contrast to some multi-valued logics , Heyting algebras share the following property with Boolean algebras: If the negation has a fixed point (i.e. for one ), Heyting algebra is trivial: it consists of only one element. ${\displaystyle \lnot a=a}$ ${\displaystyle a}$

Meaning for intuitionist logic

Arend Heyting's motivation for introducing this term was to clarify the meaning of intuitionist logic for the foundations of mathematics . The Peirce law illustrates the role that Heyting algebras for the semantics of intuitionistic logic. Peirce's law is valid in classical logic, but not in intuitionistic logic. ${\displaystyle ((P\rightarrow Q)\rightarrow P)\rightarrow P}$

A Heyting algebra is, from a logical point of view, a generalization of the usual set of truth values . Among other things, the largest element 1 of a Heyting algebra corresponds to the truth value true; the smallest element 0 corresponds incorrectly. Common two-valued logic is the simplest example of Heyting algebra - it consists of just these two elements. In abstract terms, the two-element Boolean algebra is also (like any Boolean algebra) a Heyting algebra.

Classically valid formulas are those that result in the value 1 (true) under every possible assignment of the propositional variables in two-valued Boolean algebra, i.e. H. the usual propositional tautologies . (Equivalent to this, all assignments in all Boolean algebras can be considered.) Intuitionistically valid formulas, on the other hand, are those that result in the value 1 for all Heyting algebras and all assignments. In the three-element Heyting algebra given above, the value of Peirce's law is not always 1: if one assigns ½ and 0, then the value is not 1, but only ½. According to what has been said above, this means that Peirce's law is not intuitionistically valid - but classically it is already valid. ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle ((P\rightarrow Q)\rightarrow P)\rightarrow P}$

literature

• Daniel Edwin Rutherford : Introduction to Lattice Theory ; Oliver and Boyd, 1965
• Francis Borceux: Handbook of Categorical Algebra 3 , In Encyclopedia of Mathematics and its Applications , Vol. 53, Cambridge University Press, 1994.
• G. Gierz, KH Hoffmann, K. Keimel, JD Lawson, M. Mislove and DS Scott: Continuous Lattices and Domains , In Encyclopedia of Mathematics and its Applications , Vol. 93, Cambridge University Press, 2003.
• PT Johnstone: Stone Spaces , In Cambridge Studies in Advanced Mathematics , Vol. 3, Cambridge University Press, 1986.
• Marcello Bonsangue, Bartholomeus Paulus Franciscus Jacobs, Joost N Kok: Duality Beyond Sober Spaces: Topological Spaces and Observation Frames , Vrije Universiteit, 1994.

Individual evidence

1. ^ ^{A b} D. E. Rutherford , Edward M'William Patterson : Elementary Abstract Algebra . 1965, p. 78 .