Papyrus Moscow 4676

Detail of the Moscow Papyrus (task 14), above original in hieratic script , below transcription in hieroglyphics

The Papyrus Moscow 4676 (also Moscow Papyrus or Mathematical Papyrus Moscow ) is an ancient Egyptian papyrus with mathematical content, which contains a collection of a total of 25 arithmetic problems. It is 5.44 m long and only 8 cm wide and dates back to around 1850 BC. And is one of the most important historical sources for ancient Egyptian mathematics , along with the Rhind papyrus . It is the best known of the papyri now in Moscow and was therefore given this name.

Discovery story

This papyrus was bought in 1893 by the Egyptologist Wladimir Semjonowitsch Golenishchev in Egypt and originally comes from Dra Abu el-Naga near Thebes . The Russian Egyptologist undertook a total of 60 trips to Egypt, during which he did not carry out his own excavations, and in 1911 sold his collected antiques, including the Moscow Papyrus, to the Pushkin Museum of Fine Arts in Moscow , where it is still located today with inventory number 4676.

content

The papyrus is written in hieratic script , the translation of which was published in 1930 by Wassili Wassiljewitsch Struwe and Boris Alexandrowitsch Turajew .

The papyrus contains 25 mathematical tasks that are not arranged as systematically as, for example, in the Rhind papyrus . That is why Gabriele Höber-Kamel sees the Moscow Papyrus as a kind of "examination paper" and underpins this hypothesis on the one hand with the relatively small number of tasks compared to other mathematical papyri and on the other hand with the additional comment behind the tasks, which roughly translates as: " You found out right. "

The arithmetic tasks mostly include problems with an unknown , the so-called Hau calculation .

The Egyptian hieroglyphics , initially transliterated as “Hau” and transcribed with ḥˁ.w (however “Aha (u)” in modern character reading ˁḥˁ [.w] ), means pile; Abundance; Wealth or greatness in the mathematical sense and is the ancient Egyptian term for the unknown in a calculation. In addition to a brief task, a calculation method with concrete numbers is given. Four tasks are of a geometric nature.

Exercise 6

Exercise 6 asks the question about the sides of a rectangle with a given area (12) and a given aspect ratio (3 to 4). The solution requires finding an integer square root .

Exercise 10

a sphere divided into two hemispheres

This task deals with the calculation of a basket surface. However, due to gaps in the text and the ambiguity of the symbol for "basket", the exact interpretation is controversial. In the specialist literature, inter alia, there are interpretations as the surface of a hemisphere , a half cylinder or a basket-like storage container. Regardless of the exact interpretation, the task is in any case one of the oldest written evidence of the approximate calculation of a curvilinear surface. The description given below is based on an interpretation as a hemisphere.

The following calculation formula results from the original text of this exercise, where the size d stands for the opening diameter of the basket and thus the diameter of the hemispherical bottom circle:

${\displaystyle A=2\times d\times {\frac {8}{9}}\times {\frac {8}{9}}\times d={\frac {128}{81}}d^{2}}$

In comparison, the correct formula for calculating a hemispherical surface based on current knowledge:

${\displaystyle A={\frac {1}{2}}\pi d^{2}}$ With ${\displaystyle \pi \approx 3{,}14159\ldots }$

This means that the formula corresponds to using the following approximate value for the circle number π (Pi) :

${\displaystyle \pi \approx {\frac {256}{81}}=3+{\frac {1}{9}}+{\frac {1}{27}}+{\frac {1}{81}}\approx 3{,}16049\ldots }$

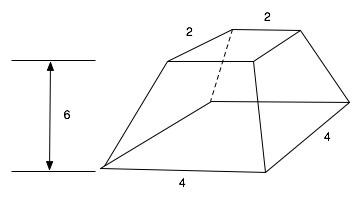
Exercise 14

Task 14 is famous, in which the volume of a square truncated pyramid is determined. The formula used is correct and in modern notation is:

${\displaystyle V={\frac {1}{3}}h(a^{2}+ab+b^{2}),}$

if a and b are the side lengths of the base and cover square and h is the height. In the exercise, the numbers a = 4, b = 2 and h = 6 are used specifically:

${\displaystyle V={\frac {1}{3}}6(4^{2}+4\times 2+2^{2})}$

This results in a volume of 56.

literature

• Wassili Wassiljewitsch Struwe, Boris Turajew: Mathematical papyrus of the State Museum of Fine Arts in Moscow (= sources and studies on the history of mathematics, astronomy and physics, Department A. Vol. 1). Springer, Berlin 1930.
• Hans Wußing : 6000 years of mathematics. Springer, Berlin a. a. 2008, ISBN 978-3-540-77189-0 , pp. 119-121.
• Hans Wußing, Wolfgang Arnold (ed.): Biographies of important mathematicians. People and Knowledge, Berlin 1975. License no. 203 1000/74 (E 00 25 05 - 1)

Web links

• John J. O'Connor, Edmund F. Robertson :  Mathematics in Egyptian Papyri. In: MacTutor History of Mathematics archive .
• Papyrus Moscow 4676 at www.meritneith.de ( Memento from August 8, 2013 in the Internet Archive )

Related topics

Other papyri of mathematical content:

• Papyrus Rhind
• Lahunpapyri

• Mathematics in Ancient Egypt
• List of papyri of ancient Egypt

Individual evidence

1. ^ Heinz-Wilhelm Alten : 4000 years of algebra. Springer, Heidelberg 2003, p. 12.
2. ↑ Guy Rachet: Lexicon of Ancient Egypt. ( Memento of the original from January 15, 2010 in the Internet Archive ) Info: The  archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. New edition, Patmos, 2002, ISBN 978-3-491-69049-3 .
3. ↑ Wassili Wassiljewitsch Struwe & Turajew (ed.): Mathematical papyrus of the State Museum of Fine Arts in Moscow. (=  Sources and studies on the history of mathematics, astronomy and physics, Section A. Sources 1). J. Springer, Berlin 1930.
4. ^ Gabriele Höber-Kamel: Astronomy in Ancient Egypt. In: Kemet 4/2000
5. ↑ http://aaew.bbaw.de/tla/servlet/s0?f=0&l=0&ff=14&hc=M35&l1=0
6. ^ Marshall Clagett: Ancient Egyptian Science: Ancient Egyptian mathematics. 1999. p. 105 ff.
7. ^ Gericke: Mathematics in antiquity and the Orient. P. 62.
8. ^ Hans Wußing : 6000 years of mathematics. Springer, Berlin a. a. 2008, ISBN 978-3-540-77189-0 , pp. 119–121, ( limited online version (Google Books) ).
9. ^ Scott W. Williams: Egyptian Mathematical Papyri. Original text and translation of Task 10 of the Moscow Papyrus
10. ↑ http://www.math.buffalo.edu/mad/Ancient-Africa/egypt_moscow14.html Original text of task 14 of the Moscow Papyrus
11. ↑ Helmuth Gericke: Mathematics in antiquity and the Orient. Springer, 1984, p. 63.