Apse (astronomy)
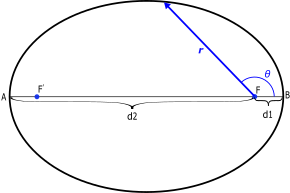
A = periapsis (d1 = periapsis
distance ) B = apoapsis (d2 = apoapsis distance)
(F, right = center of gravity = one of the two focal points )
Apse or apse ( plural apses ) in astronomy refers to one of the two main vertices of the elliptical orbit of a celestial body around another as a central body.
The apoapsis is that vertex with the greatest distance from the central body and the periapsis that with the least; both together are called apses , the straight connecting line is called the apses line .
In the case of an orbit - for example of planets - around the sun , perihelion denotes the point closest to the sun and aphelion the point furthest from the sun.
In an orbit around the earth - for example the moon - perigee denotes the point closest to the earth and apogee the point furthest from the earth.
Word origin
Apsis , as an ancient Greek word ἁψίς hapsís (in the Ionic dialect without a hint of the air, ἀψίς apsís ) means “link”, “mesh of yarn”, but most often “vault”, especially “triumphal arch” or “heavenly vault”. With the meaning "vault" it was borrowed for the term apse , which is commonly used in architecture . In astronomy, it is not only used in the sense of "(heaven) vault", but also for the apex of a trajectory. Apo and peri are prefixes with the meaning “away from a place”, “distant” or “around something”, “near”.
Derived terms
In relation to the central body
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Apses of elliptical orbits around certain central bodies are often given special names. For those related to the sun, earth or moon there are frequently used technical terms, formed from a part derived from the Greek name and the prefix Ap (o) - for the distant or Peri- for the near main vertex.
- -hel to helios " sun ": The perihelion is the closest to the sun , the aphelion the most distant point of an orbit around the sun. The earth is closest to the sun around January 3 (approx. 147.1 million km or 0.983 AU ) and furthest away around July 5 (approx. 152.1 million km or 1.017 AU). The difference of about 5 million km corresponds to an eccentricity of the earth's orbit of about 0.017.
-
-gäum to gaia " earth "; See also proximity to earth : Perigee and apogee are the closest or most distant point.
- With the moon, due to the noticeably elliptical shape of its orbit (eccentricity 0.055), the two distances 406,740 km and 356,410 km differ by over 13 percent (based on the major semi-axis of the ellipse of 384,405 km in length).
-
Artificial earth satellites : The apses of artificial earth satellites are named as well as those of the earth's moon.
- Given as the height above the earth's surface, their difference is more noticeable than when specifying geocentric distances. For example, if a circular orbit about 500 km above the earth's surface (6,371 km from the center of the earth) - were changed to an eccentricity of 0.055, the altitude would vary between 122 km and 878 km. Satellite orbits with perigees below 200 km above the earth's surface are not very stable because of the high braking effect of the atmosphere . Highly eccentric orbits are therefore created very high, such. B. the tundra orbits with apogees over 40,000 km.
- -selen to selene " moon ": periseles and aposeles are the point closest to the moon or the farthest point on the orbit of a body orbiting the moon ( English also perilune or apolune ). For example, the third lunar orbiter (1967) initially had a perisele of 210 km height and an aposele of 1790 km. After four days, the track was converted to 45 km and 1850 km in order to gain more high-resolution photos.
- -astron to aster " Star ": Periastron and Apoastron : The point on the orbit of a double star partner on which it is closest or farthest away from its companion.
- -galactic to galaxy “ Milky Way ”: Perigalactic and apogalactic are the points on the orbit of a star around the center of the Milky Way system, on which it is closest or farthest from it.
- -jovum to Latin iupiter : with Jupiter one says Perijovum and Apojovum (English Peri-, Apojove , from the Latin genitive Iovis for Jupiter ).
- -ares to Greek Ares : In Mars the apses are called Periares and Apares after the Greek deity.
- Other planets: For the other planets, Greek names would have to be added to Peri- or Apo- . Mostly they are circumscribed, analogously to the orbit of exoplanets around their central star .
More terms
Pericenter and apocenter ( Latin centrum " axis point") specifically designate points in a multi-body system and relate to its center of gravity, more precisely the barycenter . An example is the point on the orbit of a partner in a binary star system on which the partner is closest or farthest from the barycenter of the system. If the apses of an orbit are mentioned in a general celestial mechanical context without specifying a specific central body, then they can also be referred to as pericenter and apocenter , but also as perifocus and apofocus ( Latin focus " focal point ").
The distance between the system center of mass and apse is the apse distance ( Apsidendistanz ), or apse distance , so perihelion distance ( perihelion distance , often only briefly "perihelion") Apheldistanz ( Aphelabstand , "aphelion") Perizentrumsdistanz etc. Note that " Periapsis distance "(" Periapsis distance ") sometimes referred to as orbital element the angle argument of the periapsis .
The line connecting the two apses is the line of the apses .
Basics
Eccentricity and apse distance
The relationship between (numerical) eccentricity and the apsis distances is
Apses and line of apses

The straight line through the two apses is called the apse line . The line connecting the two points corresponds to the main axis of the ellipse. When calculating the path, its half size is often given as the “major semi-axis” or “mean distance”.
Orbit ellipses and barycentre
If one takes a closer look at the orbital data and averages the two apsidal distances, it is sometimes noticeable that this average distance differs from the major semi-axis . If the central body is not significantly larger than the second, the effect of the barycentre is made clear. Because not the center of the central body is in the focus of the orbit ellipse , but the barycenter as the common center of gravity of the celestial bodies .
When the system Earth-Moon the barycenter is (the Earth-Moon gravity ) nearly 5000 km from the Geozentrum , so the moon facing area of the Earth's mantle . The center of the earth therefore describes an ellipse with a diameter of 10,000 km every month.
In the case of double stars (see below) this effect is even greater and can in many cases even be recorded astrometrically . For example, a periodic change in location of the bright star Sirius was detected as early as 1800 , but its small companion was not optically detected until 1862 - as the first astrometric double star .
When detecting exoplanets with the radial velocity method, this effect is used to deduce the mass and period of orbit of the planets from the radial movement of the parent star around the barycentre.
During the passage of a body through its periapsis, it has its greatest orbital speed because up to this point - due to the decreasing orbital radius - it falls towards the center of gravity; its lowest orbital speed during its passage through the apoapsis, because up to that point it moves away from the center of gravity. The angular speed (apparent speed) in the center of the revolution changes even more because, in addition to the arc traversed in the same period of time, the distance (the radius) is also shortened - this effect is noticeable when observing the daily movement of the moon or a satellite .
Railway disruptions
In the absence of the effects of gravity from other celestial bodies and neglecting relativistic effects, an apsidal line would always have the same orientation in space. However, since the orbiting body is usually exposed to such disturbances, the apse line does not remain fixed, but rotates slowly in the direction of the orbiting celestial body. This process is called the turning of the apse . If the orbit of a celestial body shows a noticeable apse rotation, a distinction must be made between its anomalistic orbital period (return to the same apse) and its smaller sidereal period (return to the same position in relation to the fixed star background).
The disturbances from other celestial bodies can cause, in addition to the apsidal rotation, also slight, brief deformations of an orbit. The greatest and the smallest distance of this deformed path from the central body will be at slightly different places than the apses of the undisturbed path. This influences both the times when the vestibule passes and the vestibule distances involved.
Sun-earth system
In the case of the earth, its center does not revolve as with moonless planets, but the center of gravity (barycenter) shared with its moon on a Kepler ellipse around the sun. This center of gravity is still in the interior of the earth - at a depth of approx. 1700 km - but on average about 4670 km from the center of the earth. The center of the earth consequently follows a serpentine line over the ellipse.
| Perihelion passage of the earth-moon center of gravity | ||
|---|---|---|
| year | date | Sun distance ( AE ) |
| 2010 | January 3, 6 p.m. CET | 0.983314 |
| 2011 | January 4, 1 am CET | 0.983310 |
| 2012 | January 4, 04 h CET | 0.983303 |
| 2013 | January 3, 7 a.m. CET | 0.983306 |
| 2014 | January 3, 4 p.m. CET | 0.983311 |
| 2015 | January 4, 1 am CET | 0.983309 |
| 2016 | January 4, 05 h CET | 0.983296 |
| 2017 | January 3, 9 a.m. CET | 0.983297 |
| 2018 | January 3, 3 p.m. CET | 0.983312 |
| 2019 | January 3, 11 p.m. CET | 0.983273 |
| 2020 | January 4, 6 a.m. CET | 0.983253 |
Perihelion passage of the earth-moon center of gravity
The center of gravity passes through the vertex of the ellipse at mean time intervals of an anomalous year , i.e. 365 days and a good six hours. After a calendar year of 365 days has elapsed, the focus therefore needs another six hours to reach the apex again. Each round therefore takes place at a time about six hours later, until after four years a leap day brings the round forward again by one day (compare similar patterns at the beginning of the individual seasons ). However, since the leap year scheme is designed to synchronize the calendar with the tropical year and not with the anomalistic year that is about 25 minutes longer, the time of the vertex passage moves backwards through the calendar in the long term.
The table clearly shows the accumulating annual delay and the jumping back after a leap year (marked in bold). The remaining deviations from strict regularity are due to the gravitational influences of the other planets, which deform the earth's orbit slightly, so that the exact position of the point closest to the sun always moves a little back and forth.
Closest to the sun of the center of the earth
The center of the earth follows the already mentioned serpentine line over the Keplerellipse traced from the center of gravity earth / moon (barycenter). The time when the Earth is closest to the Sun is therefore generally not the time at which the Barycentre passes the vertex of the ellipse. It is also determined by the phase of the moon that exists at perihelion:
- With a waxing moon, the center of gravity of the earth reaches its closest proximity to the sun later than the barycentre, with a waning moon it is the other way round. The time difference is greatest at the half moon and can be up to 32 hours.
- If the moon is at the apex of the barycentre in the first quarter (waxing moon), the earth is moving at maximum speed towards the sun. The moon is moving away at maximum speed, the distance of the earth from the sun is still decreasing, and the maximum proximity to the sun is later than that of the barycentre. The distance of the barycenter from the sun increases after leaving the apex, but the approach of the earth to the sun caused by the moon predominates for more than a day.
- In the third quarter (waning moon) the earth was closest to the sun more than a day earlier and then moves away from the sun at maximum speed (moon at maximum speed in the direction of the sun). When the barycentre is at the apex, the earth already has a positive speed away from the sun, and the maximum proximity to the sun was earlier than that of the barycenter.
In the example for 1989 (see also figure Movement of the earth on serpentine lines around the sun ) the moon was on December 30, 1988 in the third quarter. The rapid movement of the earth away from the sun caused by it was surpassed by the relatively rapid approach of the barycentre to the sun until the night of January 1st to 2nd (about 27 hours before the apex of the barycentre on January 3rd) .
- At full moon and new moon, the center of gravity, barycentre and moon pass their elliptical vertices at about the same time. When the moon is full, the Earth's closeness to the sun is absolutely greatest and can take place exactly in the vertex. At a new moon, the closest proximity to the sun is the smallest in a mutual comparison of all moon phases and is always shortly before or after the vertex.
In the years 2010 to 2020, the closest proximity to the sun is reached a maximum of about 29 hours earlier (2016) or a maximum of about 30 hours later (2017) than the apex passage of the Baryzentrum, see table below. The earliest and latest calendar moments of the greatest closeness to the sun on earth in the years 1980 to 2020 are January 1, 1989 23 h CET (about 27½ hours before the apex passage of the Barycentre, waning moon, leap day preceding February 29, 1988) and the 5 January 2020 9 h CET (about 27 hours after the apex passage of the Baryzentrum, waxing moon, following leap day, February 29, 2020). Please note that when selecting the calendar date, because of the switching period "oscillation" of the calendar, no statement can be made about the greatest time intervals from the moment of the apex passage through the barycenter, cf. Values 1989 versus 2016 and 2020 versus 2017.
Because of the slow drift of the perihelion (rotation of the apsidal line ), these times will shift to later calendar dates. Around the year 1600 was closest to the sun between December 26th and 28th. Around the year 2500 it will fall on January 10-13.
The conditions described for the proximity to the sun also apply accordingly to the distance to the sun. The following table lists times for both cases.

Black baseline: Elliptical orbit of the center of gravity of the earth / moon.
Wavy lines: Earth orbits red (closest to the sun / "Perihel 1989" on January 1st with waning moon) and blue (closest to the sun / "Perihel 2020" on January 5th with waxing moon) with the moon influence shown 1000 times exaggerated.
| closest to the sun on earth | greatest solar distance on earth | |||||
|---|---|---|---|---|---|---|
| year | Date ( CET ) | ± | Sun distance ( AE ) | Date (CET) | Sun distance (AE) | |
| 2010 | January 3, 01 h | −17 | 0.98329 | July 6, 2 p.m. | 1.01670 | |
| 2011 | January 3, 8 p.m. | −5 | 0.98334 | July 4th 5pm | 1.01674 | |
| 2012 | January 5, 02 h | +22 | 0.98328 | July 5th 06 h | 1.01668 | |
| 2013 | January 2, 06 h | −25 | 0.98329 | July 5th 5pm | 1.01671 | |
| 2014 | January 4th 1pm | +21 | 0.98333 | July 4th 02 h | 1.01668 | |
| 2015 | January 4, 8 a.m. | +7 | 0.98328 | July 6th 10pm | 1.01668 | |
| 2016 | January 2nd 24 h | −29 | 0.98330 | July 4, 18 h | 1.01675 | |
| 2017 | January 4th 3pm | +30 | 0.98331 | July 3, 10 p.m. | 1.01668 | |
| 2018 | January 3, 7 a.m. | −8 | 0.98328 | July 6, 19 h | 1.01670 | |
| 2019 | January 3, 06 h | −17 | 0.98330 | July 4th 24 h | 1.01675 | |
| 2020 | January 5, 09 h | +27 | 0.98324 | July 4th 2pm | 1.01669 | |
Column ± : after (+) or before (-) the apex passage of the barycentre in hours
See also
Individual evidence
- ↑ Apse (1.) , in: Duden online
- ^ Wilhelm Pape , Max Sengebusch (arrangement): Concise dictionary of the Greek language . 3rd edition, 6th impression. Vieweg & Sohn, Braunschweig 1914, p. 421 ( digitized version [accessed August 13, 2018]).
- ^ Wilhelm Pape , Max Sengebusch (arrangement): Concise dictionary of the Greek language . 3rd edition, 6th impression. Vieweg & Sohn, Braunschweig 1914, p. 294 ( digitized version [accessed on August 13, 2018]).
- ^ Wilhelm Pape , Max Sengebusch (arrangement): Concise dictionary of the Greek language . 3rd edition, 6th impression. Vieweg & Sohn, Braunschweig 1914, p. 564 ( digitized version [accessed August 13, 2018]).
- ↑ http://solarsystem.nasa.gov/planets/compare (link not available)
- ↑ a b From the Ephemeridenserver HORIZONS web interface read the JPL. Observer location: "Sun (body center)", target body: "Earth-Moon Barycenter [EMB]", output of target distance "Obsrv range" and light transit time "One-Way Light-Time". Minimum distance determined by quadratic interpolation on a 10-minute grid; Corresponding point in time corrected for light transit time.
- ↑ Siegfried Wetzel: The perihelion of the earth
- ^ A b J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell. Richmond 1997. ISBN 0-943396-51-4 . Cape. 27
- ↑ a b From the Ephemeridenserver HORIZONS web interface read the JPL. Observer Location: "Sun (body center)", Target Body: "Earth [Geocenter]", output of target distance "Obsrv range" and light transit time "One-Way Light-Time". Minimum distance determined by quadratic interpolation on a 10-minute grid; Corresponding point in time corrected for light transit time. Times checked by comparison with Earth's Seasons - Equinoxes, Solstices, Perihelion, and Aphelion, 2000–2020 ( Memento of October 8, 2015 in the Internet Archive ).
- ↑ MICA 2.0: “Multiyear Interactive Computer Almanac 1800–2050”, US Naval Observatory, Washington, 2005, publ. by Willmann-Bell, Inc.



