Lagrange points
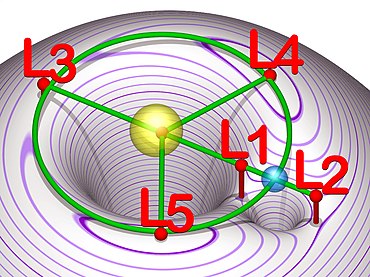
The Lagrange points or libration points (from Latin librare "to keep the balance") are five points in the system of two celestial bodies (for example a star and a planet orbiting it ) at which a light body (such as an asteroid or a space probe ) does not propel the more massive one Celestial body can orbit, whereby it has the same orbital period as the lower mass celestial body and does not change its position relative to these two. In the case of an artificial body, this is then a satellite around the more massive celestial body, but not a satellite around the lower-mass celestial body.
Mathematically speaking, the Lagrange points are the equilibrium points of the restricted three-body problem . The general three-body problem of celestial mechanics can only be solved numerically approximately. With the restriction that the third body has a negligible mass, Leonhard Euler and Joseph-Louis Lagrange found five analytical solutions: In the points named after Lagrange L 1 to L 5 , third bodies can rest without force. These are the zeros of the gravitational field in the rotating reference system in which the two heavy celestial bodies (e.g. sun and planet) also rest. This means that the gravitational forces of the two bodies on the specimen are canceled by the centrifugal force (due to the rotation of the reference system). In a non-rotating reference system, the Lagrange points run synchronously with the two celestial bodies on circular paths around the common center of gravity.
L 1 to L 3 are stable in the tangential direction and unstable in the radial direction and therefore unstable overall. L 4 and L 5 , on the other hand, are Lyapunov-stable : If the test specimen is in an area around the Lagrange point, it remains on a closed path in this area. The decisive element is the Coriolis force , which is negligible outside this environment .
Location of the Lagrange points
All five Lagrange points lie in the orbital plane of the two heavy bodies. Three lie on the connecting line of the two bodies, the fourth and the fifth form with the two bodies the corner points of an equilateral triangle (apart from relativistic corrections) . For the blue-yellow pair of celestial bodies in the above graphics, the sun and earth are used as an example.
Lagrange point L 1
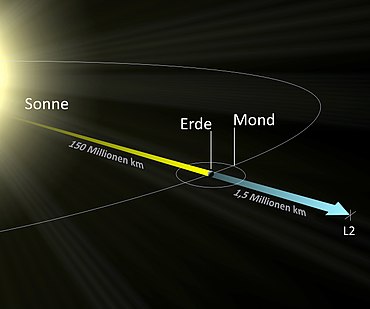
The inner Lagrange point L 1 is located between the two bodies under consideration on their connecting line. A body orbiting the sun within the earth's orbit would normally have a higher orbital speed than the earth. However, the gravitational pull of the earth weakens the gravitational pull of the sun on the body (the two forces work in opposite directions), so that in L 1 the synchronous speed of rotation is sufficient for the balance of forces. This point is almost 1.5 million km away from the earth in the direction of the sun, which corresponds to about four times the distance between the earth and the moon.

- Examples
- The inner Lagrange point L 1 in the sun-earth system serves as the "basis" for solar observation. The ISEE-3 probe set out there in 1978 and orbited it until 1982. It was the first probe to orbit a Lagrangian point. The SOHO solar observation probe has been orbiting him with a bundle of twelve measuring instruments since 1995 . From the point of view of the reference system that moves with the movement of the earth, SOHO orbits the Lagrange point once within six months at a distance of around 600,000 km in order not to be disturbed by the sun during communication and to avoid too much effort for orbit corrections. The Advanced Composition Explorer (ACE) for researching particles from all possible sources in the universe (including the sun ) has been orbiting the L 1 since the beginning of 1998. The Genesis space probe with instruments for researching the solar wind and capturing its particles was also there from 2001 to Positioned in 2004. Since 2015 the Deep Space Climate Observatory and since 2016 the LISA Pathfinder have been on a Lissajous orbit around the Lagrange point L 1 .
- The inner Lagrange point L 1 of the earth and the moon is on average about 58,000 km away from the center of mass of the moon in the direction of the earth, seen from earth about 6/7 the distance between the two celestial bodies. ARTEMIS, the extension of NASA's THEMIS missions, led to the Lagrange point L 1 of the earth and moon.
Lagrange point L 2
The outer Lagrange point L 2 is located behind the smaller of the two large bodies on their connecting line. The cause is a similar effect as in the case of the L 1 . Normally the orbit would be longer than that of the earth outside the earth's orbit. The additional attraction of the earth (forces from the sun and earth on the body are aligned), however, causes a shorter period of rotation, which in L 2 is in turn equal to the period of rotation of the earth. This point is at a distance of 1.5 million km outside the earth's orbit.
- Examples
- The L 2 point of the sun-earth system offers advantages for space telescopes . Since a body in L 2 maintains its orientation in relation to the sun and the earth, shielding it from solar radiation is much easier there than on an earth orbit. The WMAP space probe (Wilkinson Microwave Anisotropy Probe), which examined the cosmic background radiation of the Big Bang , was in an orbit around the L 2 point of the Sun-Earth system. In September 2009, ESA stationed the Herschel infrared telescope and the Planck telescope there to study background radiation. ESA's Gaia astrometry space probe has been orbiting L 2 since January 2014 . On 13 July 2019 launched a Russian Proton rocket to the X-ray telescope eROSITA the L 2 position. Even the James Webb Space Telescope is for L 2 provided.
- The outer Lagrange point of the earth and moon is on average about 64,500 km from the center of mass of the moon in the direction away from the earth. The ARTEMIS missions of NASA led, among other things, to the Lagrange point L 2 of the earth and moon. 2018 took Queqiao , a relay satellite of the Chinese Chang'e-4 mission, a halo orbit around L 2 a.
Lagrange point L 3
The Lagrange point L 3 is (as seen from the smaller body) behind the larger body on its connecting line a little outside the orbit of the smaller of the two bodies. In the case of sun-earth, the third Lagrange point is on the opposite side of the sun, almost 190 km further away from the sun than the earth. At this point the (rectified) combined gravitational pulls of the earth and the sun cause a period of rotation that is equal to that of the earth.
- example
- The L 3 point was a popular place in science fiction books and comics for a hypothetical (for us not visible due to the sun) “ counter-earth ”. However, since the mass of a "counter-earth" of the same weight in the system could no longer be neglected, this was a somewhat different three-body problem and L 3 would be exactly on the orbit of the earth for reasons of symmetry. In principle, the definition of “vanishingly small mass” would also not be fulfilled.
Lagrange points L 4 and L 5
These two Lagrangian points are each located at the third point of an equilateral triangle whose base line is the connecting line between the two large bodies. L 4 is in the direction of rotation of the smaller of the two large bodies in front of him, L 5 behind him.
If the two large bodies have very different masses, L 4 and L 5 are approximately on the orbit of the medium-sized body, 60 ° in front of or behind it.
In contrast to L 1 , L 2 and L 3 , L 4 and L 5 are stable; H. Bodies can be in their vicinity permanently even without orbit correction. Therefore, natural objects can be expected at these points. If the point L 4 or L 5 is not exactly hit, the corresponding object describes an orbit around the Lagrangian point. In fact, in the vicinity of L 4 and L 5 there are a multitude of dust clouds and small bodies, especially on the orbits of the large planets. Astronomers also call asteroids or moons in the vicinity of these points Trojans or Trojan moons . The 2010 TK 7, discovered in 2010, is in an orbit around L 4 of the earth .
Examples
- Jupiter Trojans: In the vicinity of points L 4 and L 5 of Jupiter , the Trojans (so called for the first time in Jupiter) are a group of asteroids. They have the same orbital period as Jupiter, but on average they run 60 ° ahead or behind it and periodically circle the points L 4 and L 5 in wide arcs. So far, over 3,600 and 2,000 Trojans are known in L 4 and L 5 and recorded in the asteroid lists of the Minor Planet Center , the total number is estimated at several tens of thousands. The first Trojan, (588) Achilles , was discovered by Max Wolf in 1906 . By far the largest Trojan horse is probably the (624) Hector discovered in 1907 , an irregularly shaped asteroid measuring 416 km × 131 km × 120 km in size. The Jupiter Trojans in the area of the Lagrange point L 4 are also known as Greeks.
- Trojans from other planets: In 1990 a Mars Trojan was also discovered in the libration point L 5 of Mars , which was named (5261) Eureka . Four more Mars Trojans have now been discovered, one of them in the L 4 point. At the end of 2001 a Trojan was found 60 degrees before Neptune . Taken with the 4 m reflector telescope on Cerro Tololo , it was given the provisional name 2001 QR 322 , but was only "secured" after a year. It orbits the sun - just like Neptune - in 166 earth years. In 2010 a Neptune Trojan was detected for the first time at Lagrangian L 5 , 60 ° behind Neptune, in 2008 LC 18 . Furthermore, with 2011 QF 99 a uranium trojan was found in L 4 .
- Earth companion: In 2010, astronomers from Athabasca University in Canada discovered the only known Trojan horse, the asteroid 2010 TK 7, for Earth . The discovery was published in July 2011. It moves around the Lagrange point L 4 .
In the 1950s, clouds of dust were found in the L 4 and L 5 points of the sun-earth system. In the L 4 and L 5 points of the earth-moon system , very faint dust clouds were also found, the Kordylewsk clouds , which are even weaker than the faint opposing shine. However, there are some asteroids that move around the sun in a so-called horseshoe orbit together with the earth (i.e. an average orbit period of one year). The transition from a Trojan horse to a horseshoe track is fluid: If the distance of a Trojan horse to the L 4 or L 5 point is too great, then once on the earth’s orbit it will cross the point opposite the earth and then in the direction of the other Lagrangian. Hike point. In particular, the orbit of the asteroid 2002 AA 29 (an object less than 100 m in diameter) discovered on January 9, 2002 with the help of the automatic sky monitoring LINEAR ( Lincoln Near Earth Asteroid Research ) is remarkable. It orbits the sun on an orbit very similar to the earth's orbit, whereby it describes an arc of almost 360 ° along the earth's orbit over the course of 95 years, seen from the reference system that moves with the earth's movement, which it swings back again in another 95 years. The shape of the arch is reminiscent of a horseshoe , hence the name horseshoe train. The most stable currently known horseshoe of an earth companion has (419624) 2010 SO 16 .
- Co-orbital moons ( Trojan moons ): Other Trojans are at the lunar system of Saturn . So the Saturn moon Tethys has the small moons Telesto in its L 4 - and Calypso in its L 5 point; the Saturn moon Dione has the moons Helene and Polydeuces in its L 4 and L 5 point.
Simplified model of Lagrange
Model for Lagrange points L 1 to L 3
The positions can be derived analytically if one arranges the three masses on a rotating line and demands for each of the three masses that the gravitational attraction of the other two masses keep them on a circular path. However, this leads to equations of the fifth degree .
Approximate solutions of these equations are (error in the sun-earth system approx. 0.33%, with earth-moon up to 6%):
with the distance between the two bodies with the masses and as well as . , and are the (signed) distances of the respective Lagrangian points from the heavier body of the mass .
Model for Lagrange points L 4 and L 5
If you let three bodies with the same mass rotate around each other on a common circular path, the center of mass and the center of gravity of the arrangement lie in the center of the circular path. At a certain angular velocity, which is dependent on the distance between the masses, each of the three bodies is free of forces and the system is in equilibrium. The direct gravitational effect of the three bodies on one another is balanced when the three bodies take the same distance from one another on the circular path. But this can only be the case in an equilateral triangle . There the angle of the individual sides is the same and is 60 °.
If you now change the masses, then the common center of gravity around which the system rotates is shifted towards the heaviest mass. The property that the triangle is equilateral and consequently the angles of the masses are 60 ° to each other is not influenced by this.
Derivation of the libration points by Lagrange
With comparably large masses, three bodies in a rotation system generally move chaotically around each other. It looks different if either the mass of the three bodies is the same or one of the three bodies is very small compared to the other two. Lagrange considered the latter case. The former, on the other hand, can be used well as an introduction to the understanding of the effect that leads to equilibrium in the latter case:
In his derivation, Lagrange assumed that one of the bodies should have a negligibly small mass, so that the center of mass is only determined by the two heavier bodies and lies between them; also from the fact that the two heavier ones have significantly different masses, i.e. essentially the medium-weight one (planet) orbits the heaviest one (sun). In addition to the fact that even if one of the two massive bodies is clearly the heaviest (sun), this center of mass is clearly pushed out of its center. This means, among other things, that the body with the greatest mass (sun) has to be “thrown” clearly around the common center of mass due to the interaction with the second heaviest body (planet). Exactly then and proportionally to this shift of the center of mass it happens that the two massive bodies can act past the center of gravity from opposite directions on the smallest body in the considered system - similar to the rotation system considered at the beginning with the three equally large masses, only that the angle, under which the "sun" acts on the observed small body past the center of mass, is extremely small (but nonetheless not equal to 0 ).
Now it turns out that in the case of relatively large mass ratios, firstly, a stable orbit of the three bodies is created and secondly, the structure always remains that equilateral triangle regardless of the concrete mass ratio (only that it is around a center of gravity close to the sun instead of exactly in the middle of the three bodies circling).
The model is not readily applicable to multi-planetary systems like our solar system. The deflection of the sun around its center is essentially determined by Jupiter . It is then also this planet that is the only one to have collected several mass particles around its Lagrange points L 4 and L 5 . In relation to this, all other planets deflect the sun only to a fraction, so that from their point of view the movement of the sun is overlaid by a chaotic function of high amplitude in relation to the Lagrange model. However, due to statistical effects (different orbital frequencies) and linear superposition, the Lagrange points can also have an effect on the smaller planets.
Stability of the Lagrange points

The first three Lagrangian points are only stable with regard to deviations perpendicular to the connecting line between the two large bodies, while they are unstable with regard to deviations in the direction of this connecting line. The easiest way to see this is by looking at the L 1 point. A force acts back into the equilibrium point on a test mass that is removed from L 1 along one of the red arrows perpendicular to the connecting line (in y-direction: attractive effective force). The reason for this is that the horizontal force components of the two large bodies cancel each other out, while their vertical force components add up. If, on the other hand, an object is moved a little closer to one of the other two bodies from the L 1 point (the blue arrows!), The gravitational force of the body to which it has come is greater: It therefore moves away from the equilibrium point (in x -Direction: repulsive effective force). The object behaves in a similar way to how a sphere would behave on a saddle surface , the deeper areas of which point to the two large bodies.
The points L 1 and L 2 are thus unstable, but still useful, since small corrective maneuvers of a space probe are sufficient to keep them there. Without this she would move away from these points.
In contrast, stable orbits around L 4 and L 5 are possible, provided that the mass ratio of the two large bodies is greater than 24.96. If a small body located at these points is slightly deflected, the Coriolis force brings it into a kidney-shaped orbit around this point from the point of view of the reference system in which the Lagrangian points rest. So it now remains near these points even without corrective maneuvers.
See also
- Coordinate object
- Kepler's laws
- Orbit determination
- Railway resonance
- Halo orbit
- Hill sphere
- Lissajous orbit
- Roche limit
literature
- Martin Hechler: The orbits of the Herschel and Planck space telescopes. In: Stars and Space. Heidelberg 47.2008, No. 1 (Jan.), pp. 48-55. ISSN 0039-1263
- Claudio Maccone: Page no longer available , search in web archives: Planetary defense from the nearest 4 lagrangian points plus rfi-free radioastronomy from the farside of the moon. A unified vision. Acta Astronautica, Volume 50, Issue 3, February 2002, pp. 185-199. doi : 10.1016 / S0094-5765 (01) 00176-X
Web links
- Can you park in space? from the alpha-Centauri television series(approx. 15 minutes). First broadcast on Apr 28, 2004.
- Michael Khan: Lagrange points? I beg your pardon? At: scilogs.de.
- Stefan Deiters: Genesis: An expressway through the solar system. At: astronews.com.
- Neil J. Cornish: The Lagrange Points. At: nasa.gov. Article on the topic with simple formulas and diagrams (English; PDF; 171 kB).
- Neil J. Cornish: The Lagrange Points. Montana State University , May 21, 1999, archived from the original on May 8, 2015 ; accessed on November 6, 2017 . Article on Lagrangian points with additional links.
- Gravity simulations. At: princeton.edu. Program for the simulation of multi-body systems ( Java applet ).
Individual evidence
- ↑ ZF Seidov: The Roche Problem: Some Analytics. In: The Astrophysical Journal. 603: 283-284, March 1, 2004.
- Jump up ↑ a b Jerome Pearson, Eugene Levin, John Oldson, Harry Wykes: The Lunar Space Elevator. (PDF; 365 kB), STAR Inc., Mount Pleasant, SC USA, 55th International Astronautical Congress, Vancouver, Canada, October 4-8, 2004.
- ↑ a b Notation and Numbers. Gravity 4: The Lagrange Points.
- ^ A b Mark A. Woodard, David C. Folta, Dennis W. Woodfork: ARTEMIS: The First Mission to the Lunar Libration Orbits. International Symposium on Space Flight Dynamics, January 2009.
- ↑ ESA News: ESA en route to the origins of the Universe. Retrieved May 15, 2009 .
- ↑ Gaia enters its operational orbit. ESA News, January 8, 2014, accessed January 8, 2014 .
- ↑ eROSITA launch heralds new era for X-ray astronomy. Retrieved July 15, 2019 .
- ↑ Luyuan Xu: How China's lunar satellite relay arrived in its final orbit. In: The Planetary Society. June 25, 2018, archived from the original on October 17, 2018 ; accessed on December 8, 2018 .
- ↑ List Of Jupiter Trojans. At: minorplanetcenter.net.
- ↑ Trojan asteroid: Astronomers find another companion on earth. At: spiegel.de.
- ↑ Earth's Trojan asteroid. In: Nature 475, 481-483, doi : 10.1038 / nature10233 .

![{\ displaystyle \ textstyle l_ {1} = r \ left (1 - {\ sqrt [{3 \,}] {\ frac {\ mu} {3}}} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa5d817a31cc6f29f572f52e76d3d32d9b5efbb)
![{\ displaystyle \ textstyle l_ {2} = r \ left (1 + {\ sqrt [{3 \,}] {\ frac {\ mu} {3}}} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f2200a950056ba762f7a7b734e82c3dfd9029d1)







