String theory
As string theory is defined as a collection of closely related hypothetical physical models, instead of the description of elementary particles in the usual models of quantum field theory as a point-shaped particles (spatial dimension zero) in the space-time, so-called strings ( English for threads or strings ) as fundamental properties with use one-dimensional spatial expansion. In extensions of string theory, higher-dimensional objects are also considered. String theories were introduced in the 1960s to describe the strong interaction ( quantum chromodynamics ).
String theory has experienced a strong boom since the 1980s. Since then, she has been considered the dominant candidate for a theory that unifies all natural forces and combines the standard model of elementary particle physics and gravity . The discussion is v. a. the supersymmetric version of string theory ("superstring theory"). Supersymmetry predicts new, supersymmetric partner particles for all bosons and fermions . The fact that it made concrete predictions for the symmetry groups of a Great Unified Theory (GUT) contributed significantly to the appreciation of the superstring theory . In the 1990s it turned out that the previously known superstring theories and 11-dimensional supergravity are connected with each other and are part of a more comprehensive theory (called " M-theory "), which also includes higher-dimensional objects (so-called " branes ").
String theory led to an unprecedented close exchange between different areas of pure mathematics and theoretical physics, which led to fundamental new insights, and to upheavals in the consideration of quantum field theories (such as the holographic principle in AdS / CFT ). Strings have also found applications in other areas of physics such as the description of excitations in solid-state physics and the theory of strong interaction (quantum chromodynamics).
String theory has the difficulty of making predictions that deviate from the Standard Model at the same time and that can be verified in nature and in experiment. One of the reasons for this is that the unification of natural forces is only expected on energy scales (see Planck scale ) that cannot be achieved with any known technology in the foreseeable future. String theory has therefore been criticized both inside and outside of physics since the 2000s. The criticism was also directed at the one-sided and extraordinary ties of research resources in areas that are far from applications, and was particularly decidedly by theorists who pursue alternative theories of quantum gravity (such as loop quantum gravity ). In addition, during the actual mathematical work through of the string theory, unexpectedly many variants emerged, which put the chances of success of unifying all natural forces via the string theory into the distance.
overview
In contrast to the standard model of particle physics , in string theory the fundamental building blocks that make up the world are not particles in the sense of points (i.e. zero-dimensional objects), but vibrating one-dimensional objects. These one-dimensional objects are called strings . Elementary particles can be imagined as vibrational excitation of the strings, whereby the frequency corresponds to an energy according to quantum mechanics .
In further developments of string theory, the so-called brane theories, not only one-dimensional (or, if time is included, (1 + 1) -dimensional) strings are considered as basic objects, but also higher-dimensional objects (called “branes”).
By assuming this one-dimensional structure of the strings, many desirable properties of a more fundamental theory of physics automatically emerge. What stands out most of all is that any string theory that is compatible with quantum mechanics must involve quantum gravity .
In string theory, problems are avoided that arise from diverging loop integrals and the renormalization theories developed for their compensation . Divergences (infinite values of the integrals) result especially for point particles from their self-interaction, which occurs in the case of extended, e.g. B. one-dimensional objects is "smeared" and thus softened. In simplified terms, you can imagine it as follows: If you look at Heisenberg's uncertainty principle , which is fundamental to quantum mechanics , you notice the following: If , then . This means that with a vanishing distance an infinite impulse would arise. In string theory the case is now avoided and there is an upper limit, the momentum can only have a large but finite value, in this way the divergences in theory are avoided. The uncertainty relation is modified for strings to
- with ,
where describes the string voltage. The new term is used here to define a minimum distance. This minimum distance is now given by:
If now applies, the problem of point interactions does not arise because these are excluded.
The characteristic length scale of the strings should be in the order of magnitude of the Planck length , the size under which the effects of quantum gravity become important:
On much larger length scales, such as those accessible in laboratories today, these objects would be indistinguishable from zero-dimensional point-like particles. Even so, the vibrational states and the structure of these tiny strings would make them appear as different elementary particles of the Standard Model of elementary particle physics. For example, one vibrational state of the string would be associated with a photon , another state with a quark . This unifying effect of string theory is one of its greatest strengths, but as yet no known solution to this theory accurately reproduces the multitude of particles known to the Standard Model.
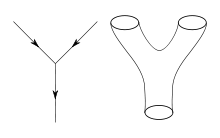
In spacetime, a particle sweeps over a line called a world line : The particle has no spatial extension, but it moves along “ time ”. A string, on the other hand, has a two-dimensional world sheet, since it also has a spatial one-dimensional expansion. The interactions of the elementary particles, described in the usual quantum field theory of point particles with Feynman diagrams in space-time, can be imagined by “thickening” these Feynman diagrams in one spatial direction (see picture above).
Types of strings
Closed and open strings
Strings can be either open or closed. A "closed string" has no end points and is therefore equivalent to a circle in its topology . An “open string” has two ends and is topologically equivalent to a segment. Not all string theories contain open strings, but every theory must contain closed strings because interactions between open strings can always create closed ones.
The oldest string theory that contained open strings was Type 1 string theory.
Characteristic types of vibration ( modes ) are always associated with open and closed strings . A particular vibration of a closed string can be identified as a graviton . In certain string theories, the oscillation with the lowest energy of an open strings, a Tachyon . Other vibrational modes open strings show the properties of photons or Gluons .
orientation
Strings can also have an "orientation" that can be thought of as an arrow within the string that distinguishes them from strings with the opposite orientation. In contrast to this, there is also the “non-oriented string” to which no such arrow can be assigned.
Bosonic String Theory
Nambu goto effect
The Nambu-Goto effect is the simplest form of the effect of a string theory, describes a bosonic string theory (without fermions) and was introduced by Yōichirō Nambu and Tetsuo Gotō around 1970 . Since the light cone quantization of the Nambu-Goto effect is not manifestly covariant , the equivalent, but more complicated Polyakov effect is available here . A point particle that moves through space-time describes a one-dimensional curve, also called a world line . Analogously, a one-dimensional string that moves through space-time describes a two-dimensional surface of the world. The world area of a string is described by a parameterization with , which can be interpreted as a time parameter and the string parameterized, applies to closed strings . Let the tangent space of the world be spanned by the vectors and . To describe the surface of the world, one can start from the analogue of the well-known Euclidean surface formula:
Since the radicand is negative in the case of the strings (higher-dimensional Minkowski space, one of the directions of the strings time-like, the other space-like), the sign still has to be changed by simply exchanging the terms; if one now uses the tangential vectors, this leads to
with the metric tensor and the formation of determinants with respect to .
After multiplication with the appropriate units in order to make the functional consistent with a physical effect, one now obtains the Nambu-Goto effect for closed and open relativistic strings in a -dimensional space-time, where the speed of light is and the string voltage introduced above:
- With
- and
The momentum densities result from:
The Nambu-Goto effect can also be written in manifest reparametrization-invariant form, whereby , in detail . This lists:
The form of this effect is also suitable for generalization to objects that have a higher dimensionality than strings, such as B. D-brane .
In comparison, the effect was for a relativistic point particle (where the sign for the term below the root sign is chosen so that the term below the root is positive for temporal world lines).
Polyakov effect
The square root of the Nambu-Goto effect has decisive disadvantages in quantization, a simpler form is the Polyakov effect, also called the String-Sigma model:
- ,
where is an additional world area metric ( ). Parametrization invariance and scaling invariance allow the auxiliary field to be chosen as, whereupon the Polyakov effect is simplified
for equations of motion in a flat Minkowski space-time.
Symmetries of the Polyakov effect
- Poincaré transformation : Global symmetry of the world surface fields with with .
- Reparametrization: The Polyakov effect is classically equivalent to the Nambu-Goto effect and therefore also locally reparametrization invariant under and .
- Weyl transformations: locally invariant under rescaling and .
Equations of motion and boundary conditions
Let us assume the motion in the flat Minkowski space-time. The equations of motion of the effect clearly describe wave equations , with vanishing energy-momentum tensor as a further limitation.
The periodic boundary conditions now apply to a closed string
- .
The Neumann boundary condition applies to an open string (string whose end points move)
- for ,
for an open string with Dirichlet boundary condition (both endpoints of the string are fixed "at the same height")
- and .
Solution of the equations of motion
To find solutions to the equations of motion, a formulation in light cone coordinates with
- with derivatives and wave equation .
Closed string
The general solution of the wave equation with boundary conditions for closed strings is given by
- ,
where the parameter was set for simplification. A closed string is called a right mover and a left mover.
Open string
The general solution for open strings with Neumann boundary conditions is given by
- .
is the position of the center of mass and the total impulse of the string; the exponential term describes the excited states.
Development to superstring theory and M-theory

Originally, the discovery of the strings (as “dual models”) was a formula by Gabriele Veneziano from 1968 within the framework of the scattering matrix theory of strongly interacting particles. In 1970 Yōichirō Nambu , Holger Bech Nielsen and Leonard Susskind gave an interpretation in the form of one-dimensional strings. Initially formulated only for particles with integer spin ( bosons ), the description of particles with half- integer spin ( fermions ) in the string model by André Neveu , John Schwarz and Pierre Ramond soon followed in 1971 . In the course of the 1970s, this resulted in the insight that there must be supersymmetry between bosons and fermions in the string models . At first there was hope of describing the strong interaction with strings , but the discovery around 1974 that the quantum theory of strings is only possible in 26 dimensions (boson string) or 10 dimensions (superstring) initially put a damper on the theory. Through the work of Joel Scherk u. a. However, it soon became clear that a superstring theory would be a candidate for a unified theory of natural forces including gravitation. In the case of closed strings, gravity results automatically as massless spin-2 excitation, the other known natural forces (all gauge theories ) correspond to massless spin-1 boson excitations. The additional dimensions would then have to be " rolled up" ( compacted ) in some way , as was the case with the Kaluza-Klein theories that have been known since the 1930s (see Kaluza-Klein compactification ).
In 1984 Michael Green and John Schwarz discovered that in superstring theories the one-loop divergences in perturbation theory only cancel each other out for very specific symmetry groups (the rotation group in 32 dimensions SO (32) and the special Lie group E8). In addition, the occurrence of “anomalies” was avoided with these symmetries, that is, a symmetry break due to quantum mechanical effects in certain interaction diagrams. This led to a revitalization of the theory and a whole series of other discoveries (so-called "First Superstring Revolution"). They showed that the theory for the gauge theories, which describe the particle spectrum in the low-energy limit case of string theory, results in considerable restrictions. In addition, Green and Schwarz explicitly constructed the first superstring theories whose existence had previously only been suspected.
In order to get a realistic model of the elementary particles in the observable 4 dimensions after the “compactification” (the “rolling in”) of the extra dimensions, Edward Witten u. a. also a number of restrictions for the compactification manifold (so-called Calabi-Yau manifolds were preferred ).
At first it was hoped to find highly restrictive principles here too, but it was discovered in the course of the 1980s that this was not the case and that the theory gave room for a very high number of possible “vacuums”.
The following five theories emerged as candidates for the superstring theories in the 1980s:
- The type I string theory , with open ends of the strings (but coupling to closed strings by contact of the ends, corresponding to gravitational interaction) and the symmetry SO (32) with charge at the ends.
- The type IIA and type IIB string theory , with closed strings; in type II A the massless fermions have both handedness (left / right), in II B only one handedness (chirality).
- Two variants of the heterotic string theory, closed strings, which are sometimes referred to as E-heterotic and O-heterotic string theory with reference to their symmetry groups E8 × E8 or SO (32). They were found by the “Princeton String Quartet” around David Gross . In them, right- and left-handed modes (RH, LH) are described by different theories: RH by a 10-dimensional superstring theory (description of bosons and fermions), LH by a 26-dimensional bosonic string theory, which compacts into 10 dimensions, whereby the Eichfeld charges arise, E8 × E8 or SO (32).
Edward Witten hypothesized in 1995 that the different types of string theory are different approximations of a more comprehensive theory, the M-theory . A complete and uniform formulation of this theory has not yet been achieved, but it is the subject of intensive research. Arguments that these theories are aspects of a single theory have been made by showing dualities between the individual string theories, that is, they have been shown to use the same system, only e.g. B. in the range of different strong coupling constants describe. Similar dualities have also been found for different solutions ("vacuums", i.e. basic states) of string theory. This was the so-called “Second Superstring Revolution”, which led to a revival of the theory, which was somewhat stagnant at the time, in the mid-1990s.
An interesting result of this unification of the partial theories was that the eleven-dimensional supergravity , which had previously fallen into isolation, was recognized as another borderline case of the M-theory. However, this does not contain any strings, but is a particle approximation of two- and five-dimensional branes. This makes it clear that a general string theory describes more than just one-dimensional strings, and in fact it was shown in the late 1990s that higher-dimensional branes ( D-branes ) play an important role in string theory ( Joseph Polchinski ).
String theory has developed into a very active research area over the years with a large number of publications per year, which is reflected in the fact that some of the researchers involved (especially Edward Witten) are among the most cited scientists in all of physics.
Experimental review
According to string theory, there is a vibration spectrum with an infinite number of vibration modes , which, however, have much too high masses ( energies ) to be observed directly. If one takes into account the small expansion of the strings in the order of magnitude of the Planck length , this means, according to a quantum mechanical standard argument , that the vibration modes have masses that are a multiple of approx. 10 19 GeV . That is many orders of magnitude higher than what can be observed today; direct evidence of these vibration modes is therefore not possible. Therefore one tries for the string theory to find specific properties for the low- energy , in comparison to the Planck mass, almost “massless” excitations. To do this, one would have to better understand the compactification mechanism from 10 or 11 to 4 dimensions - or from the Planck mass of 10 19 to the W boson mass of approx. 80 GeV or the proton mass of approx. 1 GeV - in string theory, which has not been the case so far Case is.
Nevertheless, there is already a wealth of discussed solutions for the observable low-energy sector in 4 space-time dimensions (so-called string phenomenology ).
It was expected that the experiments would e.g. B. with the Large Hadron Collider (LHC) in the 2nd half of the 2010s could provide evidence for the existence of supersymmetric particles and thus for the correctness of string theory. No supersymmetric particles had been found until 2019, and there has been no agreement among string theorists for the mechanism of supersymmetry breaking.
Another prediction of string theory is extra dimensions . For example, an axion monodromy mechanism and other possible clues to the compactification of the extra dimensions in cosmic background radiation (CMB) were discussed as a way of testing string theory . The effect of primordial gravitational waves could be reflected in patterns in the polarization of the CMB, which Bicep and other experiments are looking for, and efforts are being made to derive models of inflation potential from string theory that can then be tested in this way.
The investigation of models can also show that they are theoretically inconsistent or do not agree with generally accepted assumptions in physics. Hence, for example, boson string theory has been excluded. The general test of quantum gravity is how well a theory can microscopically explain the entropy of black holes . Various wetland hypotheses have been proposed since 2005 in order to limit the large number of possible string vacuums ( string landscape ) (initiated by Cumrun Vafa ). Wetland means areas of the string landscapes that are physically excluded . In 2018, Vafa put forward his controversial De Sitter Wetlands Hypothesis , which, if true, would lead to a contradiction with cosmological implications of string theory (and is also a problem for inflation models). It predicts a quintessential form of dark energy , which can be verified astronomically (and planned in the Dark Energy Survey ).
String theory is also used in solid-state physics, in particular via the dual description of conformal Yang-Mills theories on surfaces and string theories in the volumes enclosed by the surface in the AdS / CFT correspondence . String theory is even used in hydrodynamics ( Navier-Stokes equation in the scaling limit on the one hand, Einstein gravity as the limit case of string theory on the other hand in the dual description).
criticism
String theory has been criticized, in some cases fierce, since the 2000s. Nobel laureate and solid-state physicist Robert Laughlin , who particularly criticizes the strong ties between research resources in an area remote from application, sums it up as follows: “Far from a wonderful technological hope for a better future, string theory is the tragic consequence of an outdated belief system . “(“ Far from a wonderful technological hope for a greater tomorrow, string theory is the tragic consequence of an obsolete belief system. ”) Nobel laureate Gerard 't Hooft (2013) criticizes how representatives of competing theories on quantum gravity (such as loop quantum gravity , Carlo Rovelli , Lee Smolin ) that string theory is caught up in very conventional understandings of the role of spacetime in quantum mechanics. Carlo Rovelli criticizes string theory for proving to be non-functional and still being worked on after decades with an effort that is unparalleled (“it does not work, therefore let's develop it further”). Some critics even go so far as to deny string theory the role of a falsifiable scientific theory. For this, Peter Woit used a well-known quote from the Nobel Prize winner Wolfgang Pauli , who was known for his sharp-talkedness and who characterized theories for physical phenomena that were fundamentally not experimentally verifiable (and also not falsifiable) in such a way that they were not even wrong ( not even wrong, the title of Woits Book).
See also
literature
Popular science books
- Brian Greene : The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. Vintage Books, 2000, ISBN 0-393-05858-1 . ( The elegant universe. 2002, Goldmann Verlag, 2005, ISBN 3-442-76026-7 .)
- Brian Greene: The stuff the cosmos is made of - space, time and the nature of reality. Siedler Verlag, 2004, ISBN 3-88680-738-X . (Goldmann TB 2008; original edition The fabric of the cosmos. )
- Steven Gubser : The little book of string theory. Princeton University Press, 2010.
- Michio Kaku : In Hyperspace - A journey through time tunnels and parallel universes. Rowohlt, 1998, ISBN 3-499-60360-8 .
- Michio Kaku: The Physics of Invisible Dimensions - A journey through time tunnels and parallel universes. Rowohlt, 2013, ISBN 978-3-499-61509-2 .
- Lisa Randall : Hidden Universes - A Journey into Extra-Dimensional Space. Fischer TB, 2010, ISBN 978-3-10-062805-3 .
- Dieter Lüst : Quantum fish: The string theory and the search for the world formula. CH Beck, Munich 2011, ISBN 978-3-406-62285-4 .
- Paul Davies , Julian R. Brown: Superstrings. An all-encompassing theory of nature under discussion. DTV, 1996, ISBN 3-423-30035-3 (first 1988).
- Frederick David Peat: Superstrings, cosmic threads. Hoffmann and Campe, Hamburg 1989, ISBN 3-455-08340-4 .
From critics of string theory:
- Peter Woit : Not Even Wrong. The Failure of String Theory and the Continuing Challenge to Unify the Laws of Physics. Jonathan Cape, 2006, ISBN 0-224-07605-1 .
- Lee Smolin : The Future of Physics: Problems of String Theory and How To Go From Here . Deutsche Verlags-Anstalt, Munich 2009. See also The Trouble with Physics.
- Robert B. Laughlin : Farewell to the world formula. Reinventing physics. Piper Verlag, Munich 2007, ISBN 978-3-492-04718-0 ( A different universe - Reinventing Physics from the bottom down. Basic Books, New York, 2005.)
- Alexander Unzicker : From Big Bang to Crazy Bang: The absurd hunt for the world formula. Springer, Berlin 2010, ISBN 978-3-642-04836-4 .
- Sabine Hossenfelder : The ugly universe: Why our search for beauty leads physics to a dead end. S. Fischer 2018, ISBN 978-3-10-397246-7 ( Lost in Math: How Beauty Leads Physics Astray. Basic Books, 2018).
Textbooks
- Katrin Becker , Melanie Becker , John Schwarz : String Theory and M-Theory: A Modern Introduction. Cambridge University Press, 2007, ISBN 978-0-521-86069-7 .
- Ralph Blumenhagen, Dieter Lüst, Stefan Theisen: Basic concepts of string theory. Springer, 2013.
-
Michael Green , John Schwarz, Edward Witten : Superstring theory. Cambridge University Press, 1987.
- Vol. 1: Introduction. ISBN 0-521-35752-7 .
- Vol. 2: Loop amplitudes, anomalies and phenomenology. ISBN 0-521-35753-5 .
- Luis E. Ibáñez , Angel M. Uranga: String theory and particle physics. An introduction to String Phenomenology. Cambridge University Press, 2012, ISBN 978-0-521-51752-2 .
- Clifford Johnson : D-branes. Cambridge University Press, 2003, ISBN 0-521-80912-6 .
- Elias Kiritsis : String Theory in a Nutshell. Princeton University Press, 2007, ISBN 978-0-691-12230-4 .
- Michio Kaku : Introduction to Superstrings and M-Theory. 2nd Edition. Springer, 1999, ISBN 0-387-98589-1 .
- Dieter Lüst , Stefan Theisen : Lectures on String Theory. (= Lecture Notes in Physics. No. 346). Springer Verlag, 1989, ISBN 0-387-51882-7 .
-
Joseph Polchinski : String Theory. Cambridge University Press, 1998.
- Vol. 1: An introduction to the bosonic string. ISBN 0-521-63303-6 .
- Vol. 2: Superstring theory and beyond. ISBN 0-521-63304-4 .
- Barton Zwiebach : A First Course in String Theory. Cambridge University Press, 2004, ISBN 0-521-83143-1 .
Essays
- Michael Green: Superstrings. In: Scientific American. November 1986, ( damtp.cam.ac.uk ).
- Edward Witten: What every physicist should know about string theory. In: Physics Today. November 2015, sns.ias.edu (PDF).
Web links
- String Theory Wiki books and scripts on all areas of string theory
- Brief introduction to string theory (German)
- In Search of the Hidden Universes , Spiegel Online , February 29, 2008
- Superstrings! - Online introduction to superstring theory by John M. Pierre (English)
- The Official String Theory Web Site - String Theory Overview
- The Elegant Universe - TV documentary by Brian Greene (video available on website)
- The Elegant Universe - Interview with Sheldon Glashow on string theory
- Frank Grotelüschen : Strings in the Crisis - Physicists argue about the right path to the world formula - Deutschlandfunk - Science in focus of December 17, 2006
- Reading lists on the subject , Massachusetts Institute of Technology
- Polchinski: What is string theory? Lectures, 1994 (English), arxiv : hep-th / 9411028
Individual evidence
- ^ A b C. Rovelli: A Critical Look at Strings . In: Foundations of Physics . tape 43 , no. 1 , 2013, p. 8-20 , doi : 10.1007 / s10701-011-9599-3 .
- ^ A b 't Hooft: On the Foundations of Superstring Theory . In: Foundations of Physics . tape 43 , no. 1 , 2013, p. 46-53 , doi : 10.1007 / s10701-012-9682-4 .
- ↑ After the English ending of membrane, with an echo of the English word "brain" for brain. First two-dimensional objects were discussed, the membranes, later also higher-dimensional p-branes, especially the D-branes , in which the D stands for Dirichlet boundary condition.
- ^ Lectures by Nambu at a symposium in Copenhagen in August 1970, published in Nambu, Selected Papers, 1995.
- ↑ Tetsuo Gotō: Relativistic quantum mechanics of one dimensional mechanical continuum and subsidiary condition of dual resonance model. In: Progress Theoretical Physics. Volume 46, 1971, p. 1560.
- ↑ e.g. measured with the H index .
- ↑ See e.g. B. Jan Louis: The many strings of string theory. In: Physics Journal. Volume 7, 2008, No. 6, pp. 29-35.
- ↑ See for example Luis E. Ibáñez, Angel M. Uranga: String theory and particle physics. An introduction to String Phenomenology. Cambridge University Press, 2012.
- ↑ A range of experiments at CERN investigate physics from cosmic rays to supersymmetry. CERN, accessed August 12, 2016 .
- ^ Gary Shiu, Bret Underwood: Observing the Geometry of Warped Compactification via Cosmic Inflation. In: Physical Review Letters. Volume 98, 2007, 051301, arxiv : hep-th / 0610151 .
- ↑ Horatiu Nastase: String theory methods in condensed matter physics. Cambridge UP 2017
- ↑ String theory: Is it science's ultimate dead end? In: The Guardian . October 8, 2006 ( theguardian.com ).