Steradian
| Physical unit | |
|---|---|
| Unit name | Steradian |
| Unit symbol | |
| Physical quantity (s) | Solid angle |
| Formula symbol | |
| dimension | |
| system | International system of units |
| In SI units | |
| Named after | Greek στερεός , "spatial" and Latin radius , "ray" |
| Derived from | Radians |
| See also: square degrees | |
The steradian , also sterad , unit symbol sr , is a unit of measurement for the solid angle . In the SI system of units , it is included as a derived unit of measurement.
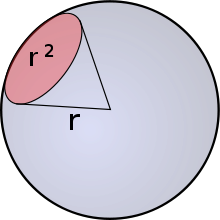
On a sphere with a 1 m radius, a steradian encloses an area of 1 m² on the surface of the sphere . The solid angle of the entire spherical surface is 4π sr.
definition
A sphere with the radius is given . Then a steradian is the solid angle that a spherical cap assumes with the area on the spherical surface when viewed from the center of the sphere . This solid angle can be calculated as the area of the spherical cap divided by the square of the radius :
The division has the effect that the solid angle does not depend on the radius of the sphere under consideration.
- example
The solid angle of a cone, which cuts a partial area ( ) of 13.5 m 2 from a sphere with a radius of 3 m , is .
If the solid angle relates to a circular cone from the center of the sphere, as in the figure on the right ( canonical solid angle ), it can be viewed as a plane angle in the section through the center of the sphere . The following relationship can be derived from the relationship for the area of the spherical cap of the cone and the angle :
- .
The opening angle of a cone that covers the solid angle 1 sr is approx. 65.54 °.
history
In the SI, it was initially left open whether steradian and radian are derived units or base units; the class of “complementary units” was created for both. In 1980 the CIPM recommended that these supplementary units be interpreted as derived. This was followed in 1995 by the 20th General Conference on Weights and Measures (CGPM) and resolved in resolution 8 to abolish the class of supplementary units.
The unit symbol "sr" was established in 1950 by the CIPM. In the past, the characters “str” and “sterad” were also used.
See also
Web links
Individual evidence
- ^ Resolution 8 of the 20th CGPM (1995). In: bipm.org. Bureau International des Poids et Mesures, accessed September 30, 2019 .