Length of the ascending node
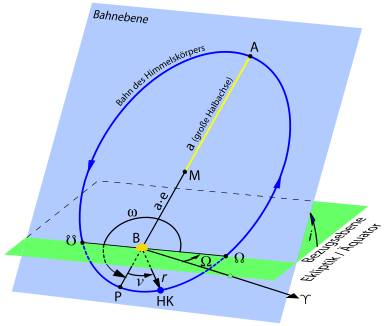
Six orbit elements
a : Length of the major semi-axis
e : Numerical eccentricity
i : Orbital inclination, inclination
Ω: Length / right ascension of the ascending node
ω: Argument of the periapsis, periapsis distance
t : Time of the Periapsis passage, periapsis time, epoch of the periapsis passage
Further designations
M: Ellipse center. B: focus, central body, sun / earth. P: periapsis. A: Apoapsis. AP: apse line. HK: Celestial body, planet / satellite. ☋: descending node. ☊: ascending node. ☋☊: knot line. ♈: spring equinox. ν: true anomaly. r: distance of the celestial body HK from the central body B
In celestial mechanics, the length of the ascending node ( node length for short ; symbol Ω ) of an orbit around the sun is the heliocentric angle to be measured in the ecliptic ( reference plane or reference plane) between the ascending node ☊ and the spring point ♈.
The length of the ascending node is one of the six orbit elements (see graphic) that suffice for a sufficient description of an - ideal - Kepler orbit. Together with the inclination i and the argument of the periapsis ω , it belongs to that subgroup of orbit elements that defines the position of the orbit plane in space .
Other central bodies or reference planes
In the case of central bodies other than the sun and / or other reference planes than the ecliptic, “length” generally means the first polar coordinate of a spherical coordinate system .
Depending on the type of object whose path is specified, they, the following reference are flat usual:
- for solar orbital objects of the solar system , d. H. for planets , asteroids , comets : the ecliptic
- where the length of the ascending node is its ecliptical length ( longitude of the ascending node, LOAN ), measured from the vernal equinox .
- for objects that do not orbit the sun: the equatorial plane of the central body that the object orbits instead; For example, for earth satellites with a uniform orbit semi-axis : the plane of the earth or celestial equator (see satellite orbit elements ).
- where the length of the ascending node is its right ascension (i.e. the equatorial length, English right ascension of the ascending node, RAAN ), again measured from the vernal equinox, but this time along the equator.
- for the earth's moon : the ecliptic
- where the length of the ascending node is its ecliptical length , measured geocentrically from the vernal equinox .
Time dependence
In the case of Kepler orbits (only two bodies in a vacuum ) the length of the knot is constant and the orbital plane remains stable in its alignment under the fixed stars .
In the case of gravitational disturbances from third bodies , the length of the node suffers small, sometimes periodic changes. The orbit element is therefore given as a series of oscillating terms with respect to an epoch , i.e. as an approximate solution that is valid at a certain point in time .
As a first approximation, the value for the length of the lunar knot is given as
- with T as time argument in Julian centuries since the epoch J2000.0 ( Lit .: Vollmann, 3.5 p. 26).
The approximately 19.34 ° in a Julian year (365.25 days) correspond to one complete rotation of the knot line in 18.61 years, the nutation period .
literature
- Andreas Guthman: Introduction to celestial mechanics and ephemeris calculation , theory, algorithms, numerics , 2nd edition. Spectrum Academic Publishing House, 2000
- Jean Meeus: Astronomical Algorithms . Willmann-Bell Inc., 2009
- Wolfgang Vollmann: Changing star locations . In: Hermann Mucke (Hrsg.): Modern astronomical phenomenology. 20th Sternfreunde Seminar, 1992/93. Planetarium of the City of Vienna - Zeiss Planetarium of the City of Vienna - Zeiss Planetarium and Austrian Astronomical Association , 1992, pp. 55–102 ( online )
