Geosynchronous orbit

A geosynchronous orbit is a satellite orbit in which the orbital time around the earth coincides exactly with the period of rotation of the earth ( sidereal day ); the satellite orbits the earth synchronously with the rotation of the earth, but not necessarily synchronously at every point in time. Since the synchronicity does not necessarily apply to every point in time of the orbit, the satellite with eccentricities ≠ 0 can temporarily lead or lag laterally for an observer on the earth's surface and ascend or descend for orbital inclinations ≠ 0 °. In the special case of geostationary orbit (orbit inclination = 0 ° and eccentricity = 0), however, a satellite is always at the same point in the sky for the observer.
Since pre-travel and post-travel and up and down movement react very sensitively to disturbances of the orbit inclination and eccentricity, orbital disturbances caused by the gravitational influences of the sun and moon and the anisotropy of the earth's gravitational field are particularly noticeable in geosynchronous orbits. Satellites positioned there need fuel to correct the orbital disruptions . This alone means that they only have a limited lifespan .
Uses geostationary satellites are mainly in the field of communication , but also weather satellites take advantage of this orbit.
Orbit classes
Geosynchronous orbits have angles of inclination from 0 ° (geostationary) through 90 ° ( polar orbit ) to 180 ° ( retrograde , i.e. counterrotation to the rotation of the earth).
Inclined orbit
If the inclination is different from 0 °, the orbit is called inclined geosynchronous orbit, English inclined geosynchronous orbit (IGSO) .
Depending on the orbit inclination or angle of inclination, a distinction is made:
- Low inclination orbits are used under the name Inclined Orbit by former geostationary communications satellites to extend their lifespan when their fuel reserves are almost depleted . However, because their position in the sky then fluctuates, such satellites can only be received with professional antennas with antenna tracking.
- The Quasi-Zenith Satellite System (QZSS) is a four-satellite system used to improve satellite navigation systems in Japan. The satellites stand on a 45 ° inclined orbit with an eccentricity of 0.09 and a perigee angle ( argument of the perigee ) of 270 ° for eight hours, almost vertically above the island.
- Highly elliptical orbits of large inclination are also called tundra orbits .
Geostationary orbit
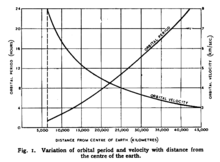
The special case of a circular orbit with an easterly direction of rotation and an orbit inclination of 0 ° is called geostationary. The orbit speed is always 3.075 kilometers per second (11,070 km / h), and the orbit radius is 42,164 km. After subtracting the equatorial radius of about 6,378 km, this corresponds to a distance of about 35,786 km to the earth's surface.
When viewed from Earth, a geostationary satellite appears to be standing still in the sky (it is "stationary") because it moves at the same angular velocity as the observer on Earth. Because of this, this orbit is widely used for television and communications satellites. The antennas on the ground can be fixed to a specific point, and each satellite always covers the same area of the earth. However, these satellites usually focus their antennas on individual regions ( coverage areas ), so that the signals can usually only be received in the broadcast areas.
Formulas
To keep a body of mass with angular velocity on a circular path with the radius , a centripetal force is the strength
required. On a circular orbit around a planet, gravity is approximately the only effective force. At a distance - starting from the center of the planet - you can use the formula
be calculated. It denotes the gravitational constant and the mass of the planet.
Since gravity is the only force that keeps the body on the circular path, its value must correspond to the centripetal force. The following applies:
By inserting it results:
Solving for gives:
The angular frequency results from the period of rotation as:
Inserting it into the formula for gives:
This formula now determines the radius of the geostationary orbit of a center of mass starting from the center of the planet under consideration.
In order to get the distance of the orbit from the surface of the planet - for example the height of a geostationary satellite above the earth's surface - its radius has to be subtracted from the result. So we have:
where denotes the radius of the planet.
If the planet has a satellite (e.g. moon) with known orbit data, the third law of Kepler can also be used as an alternative
apply to satellite and geostationary satellite.
In the example of a terrestrial satellite, the orbit data of the earth's moon can be used (orbit duration T moon ≈ 655 h, major semiaxis of the lunar orbit r moon ≈ 384,000 km, T Sat = 23 h 56 min). Solved for the orbit radius of the geostationary satellite, which is equal to the orbit radius because of the circular orbit, this results in:
The height above the surface of the planet, here the earth, is again obtained by subtracting the planet's radius.
history
The idea of a geostationary satellite was first published by Herman Potočnik in his 1928 book The Problem of Navigating Space - The Rocket Motor .
In 1945, science fiction writer Arthur C. Clarke proposed placing satellites in geostationary orbit. Worldwide radio communication would be possible with three satellites, each offset by 120 °. He assumed that satellites could be positioned there within the next 25 years. With Syncom 2 in geosynchronous orbit in 1963 and Syncom 3 in geostationary orbit in 1964, his idea was realized much more quickly, after about 19 years.
The picture to the right shows the diagram in which Clarke first presented his ideas to the public in Wireless World magazine .
See also
Web links
- Orbit of a satellite in GEO ( Memento from March 2, 2009 in the Internet Archive )
- Book scan: The problem of navigating space. The rocket engine. by Herman Potočnik alias Hermann Noordung. accessed on January 21, 2020











![r = {\ sqrt [{3}] {G {\ frac {M} {\ omega ^ {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c785540b85e490d5f41a232cd512464c74565578)


![r = {\ sqrt [{3}] {{\ frac {G} {4 \ pi ^ {2}}} Mt ^ {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0a09bbe750b22eef35eab61753d2efe4116b33e)
![h = {\ sqrt [{3}] {{\ frac {G} {4 \ pi ^ {2}}} Mt ^ {2}}} - R_ {P}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f838c9449db7282304191a716d6af2bedb7a735)


![{\ displaystyle r _ {\ text {Sat}} = {\ sqrt [{3}] {\ frac {r _ {\ text {Moon}} ^ {3} \ cdot T _ {\ text {Sat}} ^ {2} } {T _ {\ text {moon}} ^ {2}}}} \ approx 42000 \, \ mathrm {km}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2af19c32d3e0fae832bad2d8b68fd501fbaad84)