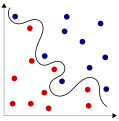
Linear separability

• 

  Two non-linearly separable relations in . ${\displaystyle \mathbb {R} ^{2}}$

• 

  Two linearly separable relations in . ${\displaystyle \mathbb {R} ^{2}}$

Linear separability (also separability , or classifiability ) describes in mathematics the property of two relations ( sets of - tuples ) for which a hyperplane (or a linear discriminant function ) exists, which separates them in the -dimensional vector space . ${\displaystyle n}$ ${\displaystyle n}$

In 2-dimensional space this means that a straight line can be laid between two linearly separable point sets.

Formal definition

Two subsets are called linearly separable if real numbers exist, so that for all the inequalities ${\displaystyle A\subseteq \mathbb {R} ^{n},B\subseteq \mathbb {R} ^{n}}$ ${\displaystyle n+1}$ ${\displaystyle w_{1},\dotsc ,w_{n+1}}$ ${\displaystyle {\vec {a}}=(a_{1},\dotsc ,a_{n})\in A,{\vec {b}}=(b_{1},\dotsc ,b_{n})\in B}$

${\displaystyle \sum _{i=1}^{n}w_{i}a_{i}\leq w_{n+1}<\sum _{j=1}^{n}w_{j}b_{j}}$

be valid. The points from , for which applies, form the separating hyperplane. ${\displaystyle {\vec {x}}=(x_{1},\dotsc ,x_{n})}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \textstyle \sum _{i=1}^{n}w_{i}x_{i}=w_{n+1}}$

Functions that can be linearly separated

Linear separability of functions

Binary functions (i.e. with ) are called linearly separable if the archetypes of 0 and 1 are separable. The linearly separable functions play a role especially in machine learning . For example, the simple perceptron can only learn linearly separable functions. ${\displaystyle f\colon D\rightarrow \{0,1\}}$ ${\displaystyle D\subseteq \mathbb {R} ^{n}}$

An example of a function that cannot be linearly separated is the XOR link . As the diagram shows, a linear separation of the two result values ​​is not possible.

See also

The linear separability of disjoint convex sets , which is plausible in the 2- or 3-dimensional visual space, is treated in the separation theorem . This also includes generalizations to infinite-dimensional spaces.

Separability as a property of filters in image processing should not be confused with linear separability.