Copula (mathematics)

A copula (Pl. Copulas or copulas ) is a function that a functional relationship between the marginal distribution functions of various random variables and their joint probability distribution may indicate.

With their help, one can model stochastic dependency much more flexibly than, for example, with correlation coefficients .

definition

A copula is a multivariate distribution function whose one-dimensional marginal distributions are uniformly distributed over the interval . Expressed formally this means the following: ${\displaystyle C\colon [0,1]^{n}\rightarrow [0,1]}$ ${\displaystyle [0,1]}$

• ${\displaystyle C}$ is multivariate distribution function, that is
  • ${\displaystyle \forall u\in [0,1]^{n}\colon \min\{u_{1},\dotsc ,u_{n}\}=0\implies C(u)=0}$,
  • ${\displaystyle C}$is -increasing, i.e. for every hyper-rectangle the -volume is not negative:, where , ${\displaystyle n}$ ${\displaystyle R=\prod _{i=1}^{n}[x_{i},y_{i}]\subseteq [0,1]^{n}}$ ${\displaystyle C}$ ${\displaystyle V_{C}\left(R\right):=\sum _{\mathbf {z} \in \prod _{i=1}^{n}\{x_{i},y_{i}\}}(-1)^{N(\mathbf {z} )}C(\mathbf {z} )\geq 0}$ ${\displaystyle N(\mathbf {z} ):=|\{k\mid z_{k}=x_{k}\}|}$

• The one-dimensional marginal distributions of are uniform on the unit interval: . ${\displaystyle C}$ ${\displaystyle \forall j\in \{1,\dotsc ,n\},u=(u_{1},...,u_{n})\in \{1\}^{j-1}\times [0,1]\times \{1\}^{n-j}\colon C(u)=u_{j}}$

The requirement for the marginal distributions can be motivated as follows: For randomly distributed random variables with continuous distributions , the random variable is uniformly distributed over the interval . Together with the following theorem by Sklar, the separation of marginal distributions and dependencies among them becomes possible. ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$ ${\displaystyle F_{X_{i}},\;i\in \{1,2,\dotsc ,n\}}$ ${\displaystyle F_{X_{i}}(X_{i})}$ ${\displaystyle [0,1]}$

Sklar's theorem

The following is an extension of the real numbers . ${\displaystyle {\overline {\mathbb {R} }}:=\mathbb {R} \cup \{-\infty ,+\infty \}}$

Let be a -dimensional distribution function with one-dimensional marginal distributions . Then there is a -dimensional copula , so that for all it holds: ${\displaystyle F:{\overline {\mathbb {R} }}^{n}\rightarrow [0,1]}$ ${\displaystyle n}$ ${\displaystyle F_{1},\ldots ,F_{n}:{\overline {\mathbb {R} }}\rightarrow [0,1]}$ ${\displaystyle n}$ ${\displaystyle C}$ ${\displaystyle (x_{1},\ldots ,x_{n})\in {\overline {\mathbb {R} }}^{n}\ }$

${\displaystyle F(x_{1},x_{2},\ldots ,x_{n})=C\left(F_{1}\left(x_{1}\right),\ldots ,F_{n}\left(x_{n}\right)\right).}$

If all are continuous, the copula is unique. ${\displaystyle F_{i}}$

Fréchet-Hoeffding barriers

For every -variate copula the lower Fréchet-Hoeffding bound applies ${\displaystyle n}$ ${\displaystyle C}$

• ${\displaystyle C(u_{1},\ldots ,u_{n})~\geq ~\max \left\{\sum \limits _{i=1}^{n}{u_{i}}+1-n,~0\right\}~=:~W(u_{1},\ldots ,u_{n})}$

and the upper Fréchet-Hoeffding barrier

• ${\displaystyle C(u_{1},\ldots ,u_{n})~\leq ~\min\{u_{1},\ldots ,u_{n}\}~=:~M(u_{1},\ldots ,u_{n})}$

The upper bound is itself a copula, whereas the lower bound is only for . ${\displaystyle M}$ ${\displaystyle W}$ ${\displaystyle n=2}$

application

Copulae are used to draw conclusions about the type of stochastic dependence of various random variables or to model dependencies in a targeted manner. They are used, for example, in credit risk analysis in order to be able to make statements about the accumulated bankruptcy of several debtors within a bond portfolio. Similarly, applications are common in the insurance sector. Accumulated damage of various types of damage poses a financial problem there. An example of this is an observable connection between storm damage and flood damage. Another central application in the field of financial mathematics is the modeling of operational risks and the modeling of the dependencies between the types of risk (credit and market risk, insurance risk and credit risk, etc.).

Examples of copulae

• The simplest form of the copula is the independence copula (product copula )

${\displaystyle C(u_{1},\ldots ,u_{n})=\prod \limits _{i=1}^{n}u_{i}=u_{1}\cdot \ldots \cdot u_{n}}$.

It stands for stochastically independent random variables that are distributed according to Copula C. In characters: ${\displaystyle U_{1},\ldots ,U_{n}}$ ${\displaystyle (U_{1},\ldots ,U_{n})\sim C}$

• The upper Fréchet-Hoeffding bound, also a copula, is given by

${\displaystyle C(u_{1},\ldots ,u_{n})=\min _{i=1,\ldots ,n}u_{i}}$.

It describes perfect positive stochastic dependence (total positive correlation).

• The lower Fréchet-Hoeffding bound is only a copula in the bivariate case:

${\displaystyle C(u_{1},u_{2})=\max\{u_{1}+u_{2}-1,0\}}$.

It describes a perfect negative stochastic dependence of two random variables.

• The normal or Gaussian copula is defined with the help of the distribution function of the normal distribution . So is ${\displaystyle F(\cdot )}$

${\displaystyle C(u_{1},u_{2})=F_{2}(F^{-1}(u_{1}),F^{-1}(u_{2}),\rho )\,}$

a copula, where is the bivariate distribution function of two standard normally distributed random variables with the correlation coefficient . ${\displaystyle F_{2}(\cdot ,\cdot ,\rho )}$ ${\displaystyle \rho }$

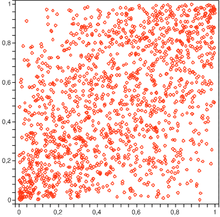
If you create points that are distributed according to the normal copula with parameters , there is already a slight concentration of these along the bisector. ${\displaystyle \rho =0.5}$

Simulation of the bivariate normal copula, rho = 0.5, 1500 points

• The Gumbel copula is defined using the exponential function and the natural logarithm

${\displaystyle C_{\lambda }(u_{1},u_{2})=\exp \left(-\left(\left(-\ln u_{1}\right)^{\lambda }+\left(-\ln u_{2}\right)^{\lambda }\right)^{1/\lambda }\right)}$,

where a fixed parameter is to be selected. ${\displaystyle \lambda \geq 1}$

If points are generated which are distributed according to the Gumbel copula with parameters , a point clustering results in particular in the vicinity of the point . ${\displaystyle \lambda >1}$ ${\displaystyle (1,1)}$

Simulation of the bivariate Gumbel copula, lambda = 2, 1500 points

Archimedean copulae

Archimedean copulae represent a class of copulae. These can be described as follows:

Let be a continuous, strictly monotonically decreasing function with . Denote the pseudo-inverse of , i.e. H. ${\displaystyle \varphi \colon [0,1]\rightarrow [0,\infty ]}$ ${\displaystyle \varphi (1)=0}$ ${\displaystyle \varphi ^{[-1]}\colon [0,\infty ]\rightarrow [0,1]\ }$ ${\displaystyle \varphi }$

${\displaystyle \varphi ^{[-1]}(t):={\begin{cases}\varphi ^{-1}(t),&{\textrm {falls}}\ 0\leq t\leq \varphi (0)\\0,&{\textrm {sonst}}\end{cases}}}$

A bivariate function can now be defined with the help of and : ${\displaystyle \varphi }$ ${\displaystyle \varphi ^{[-1]}}$

${\displaystyle C\colon [0,1]^{2}\rightarrow [0,1],\quad C(u,v):=\varphi ^{[-1]}\left(\varphi \left(u\right)+\varphi \left(v\right)\right)}$

The function is a copula if and only if is convex. In this case the copula is called the producer or generator . Obviously, it is symmetrical, i.e. H. for everyone . ${\displaystyle C}$ ${\displaystyle \varphi }$ ${\displaystyle \varphi }$ ${\displaystyle C}$ ${\displaystyle C(u,v)=C(v,u)}$ ${\displaystyle u,v\in [0,1]}$

Examples of Archimedean copulae are:

• Gumbel copula : Its generator is the function with parameters . ${\displaystyle \varphi (t)=(-\ln t)^{\lambda }}$ ${\displaystyle \lambda \geq 1}$

This results in and with it the Gumbel copula as above. ${\displaystyle \varphi ^{[-1]}(t)=\exp \left(-t^{\frac {1}{\lambda }}\right)}$ ${\displaystyle C_{\lambda }(u,v)}$

• Clayton copula : Its generator is the function with parameters . ${\displaystyle \varphi (t)={\frac {1}{\Theta }}\left(t^{-\Theta }-1\right)}$ ${\displaystyle \Theta >0}$

Hence, and the bivariate Clayton copula results in: ${\displaystyle \varphi ^{[-1]}(t)=\left(\Theta \cdot t+1\right)^{-{\frac {1}{\Theta }}}}$

${\displaystyle C(u,v)=\left(u^{-\Theta }+v^{-\Theta }-1\right)^{-{\frac {1}{\Theta }}}}$

• Frank-Copula : Its producer is the function with parameters . ${\displaystyle \varphi (t)=-\ln \left({\frac {e^{-\Theta \cdot t}-1}{e^{-\Theta }-1}}\right)}$ ${\displaystyle \Theta >0}$

Archimedean copulae are often used because it is very easy to generate random numbers from them.

Extreme value copula

definition

A copula is called an extreme value copula if it is the copula of a multivariate extreme value distribution , ie there is a multivariate extreme value distribution with univariate margins that applies . ${\displaystyle C}$ ${\displaystyle G}$ ${\displaystyle G_{1},\dots ,G_{n}}$ ${\displaystyle C(u_{1},\dots ,u_{n})=G(G_{1}^{-1}(u_{1}),\dots ,G_{n}^{-1}(u_{n}))}$

lemma

A copula is exactly then Extremwertcopula if for and apply . ${\displaystyle C}$ ${\displaystyle \mathbf {0} \leq \mathbf {u} =(u_{1},\dots ,u_{n})^{T}\leq \mathbf {1} }$ ${\displaystyle t>0}$ ${\displaystyle C(u_{1}^{t},\dots ,u_{n}^{t})=C^{t}(u_{1},\dots ,u_{n})}$

If there is an extreme value copula and there are univariate extreme value distributions , then there is a multivariate extreme value distribution. ${\displaystyle C}$ ${\displaystyle G_{1},\dots ,G_{n}}$ ${\displaystyle G((x_{1},\dots ,x_{n})^{T}):=C(G_{1}(x_{1}),\dots ,G_{n}(x_{n}))}$

Relationship between copula and T-norm

Every bivariate associative and commutative copula is a T-norm (see Grabisch et al. 2009). For example, the bivariate product copula and both bivariate Fréchet-Hoeffding bounds are T-norms at the same time.

literature

• Harry Joe: Dependence Modeling with Copulas (Monographs on Statistics and Applied Probability 134). CRC Press, 2015, ISBN 978-1-4665-8322-1 .

• J.-F. Mai, M. Scherer: Simulating Copulas (Stochastic Models, Sampling Algorithms and Applications). World Scientific, 2012, ISBN 978-1-84816-874-9 .

• J. Wernz: Bank Management and Control. Springer Nature, 2020, ISBN 978-3-03042865-5 .

• Roger B. Nelsen: An Introduction to Copulas. (= Lecture Notes in Statistics ). Springer Verlag, 2006, ISBN 0-387-28659-4 .

• A. Sklar: Random variables, distribution functions, and copulas - a personal look backward and forward. In: L. Rüschendorf, B. Schweizer, M. Taylor (Eds.): Distributions With Fixed Marginals & Related Topics. (= Lecture Notes - Monograph Series Number. 28). 1997, ISBN 0-940600-40-4 .

• Rico Fischer: Modeling of dependencies with the help of copulas: application in the determination of the Value at Risk. Logos Berlin, 2009, ISBN 978-3-8325-2142-4 .

• Grabisch, M., Marichal, J.-L., Mesiar, R. and E. Pap: Aggregation Functions . Cambridge University Press 2009. ISBN 978-0-521-51926-7 . P. 56f. ( limited preview in Google Book search)

Web links

• P. Embrechts, F. Lindskog, A. McNeil: Modeling Dependence with Copulas and Applications to Risk Management. In: S. Rachev (Ed.): Handbook of Heavy Tailed Distributions in Finance. Elsevier, Chapter 8, 2003, pp. 329-384. (people.math.ethz.ch ; PDF; 818 kB)

• P. Embrechts, A. McNeil, D. Straumann: Correlation and dependence in risk management: properties and pitfalls. In: MAH Dempster: (Ed.): Risk Management: Value at Risk and Beyond. Cambridge University Press, Cambridge 2002, pp. 176-223. (people.math.ethz.ch ; PDF; 784 kB)

• C. Schölzel, P. Friederichs: Multivariate non-normally distributed random variables in climate research - introduction to the copula approach. In: Nonlinear Processes in Geophysics. 15, 2008, pp. 761-772. (www.nonlin-processes-geophys.net open access)

• Andreas Beck, Michael Lesko, Frank Schlottmann, Konrad Wimmer: Copulas in risk management. In: Journal for the entire credit system. 14/2006. (risknet.de)

• Michael Lesko, Andreas Beck: For modeling dependencies in banking practice - copula functions for determining the overall bank risk profile. In: Business sheets. 5/2006. (risknet.de)