Overlay (topology)
Overlays are examined in the mathematical sub-area of topology . An overlay of a topological space consists of a further topological space, the overlay space, and a continuous mapping that maps from the overlay space into the starting space and has certain properties.
One can clearly imagine an overlay in such a way that one unrolls the exit space on the overlay space or wraps the exit space with the overlay space.
definition
Be a topological space . An overlay of is a topological space together with a continuous surjective mapping
so that to each point in an environment are, for the archetype among from a union of pairwise disjoint open sets which each have means homeomorphic to be imaged.
Often the term overlay is used for both overlay space and overlay mapping. For an in , the fiber is called by . It consists of finitely or infinitely many discrete points. In the first case one speaks of a finite superposition .
It is said that the elements of the fiber above . The open quantities are called leaves .
Examples
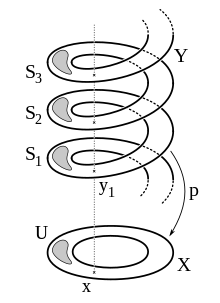
Look at the unit circle in . The real straight line is then an overlay with the overlay image
- .
The straight line is wrapped around the circle infinitely often. The leaves above an interval of the circle are intervals on the number line that repeat with period . Every fiber has an infinite number of elements ( ). The isomorphism between the fundamental group of and the additive group over the whole numbers can be demonstrated very clearly with the help of this superposition.
The complex plane without the origin ,, is superimposed by itself on the image
- .
Every fiber here has elements.
An example from quantum mechanics concerns the group SO (3) of the rotations of three-dimensional real space . The SU (2), ie the group of "complex rotations" of the , the so-called spinor group, belongs to it as a "double" superposition . In contrast to SO (3) it is simply connected .
properties
Each overlay is a local homeomorphism , that is, the restriction of the overlay mapping to a small neighborhood is a homeomorphism to an open subset. Therefore possess and the same local properties:
- if is a manifold , then so does every connected covering of .
- if is a Riemann surface , then this is also every superposition of and is then holomorphic .
- if is a Lie group , so is every superposition of , and is then a Lie group homomorphism .
- if there is a CW complex , so does every superposition of .
For each connected component of the number of elements of a fiber over a point (and thus the number of leaves over a neighborhood) is always the same. If every fiber has elements, one speaks of a -fold overlay .
The elevation property applies: if there is an overlay, a path in and a point above the starting point (i.e. ), then there is a unique path in via (i.e. ) with a starting point . Paths in can therefore be clearly lifted up from the fiber if a starting point is specified .
If and are two points in which are connected by a path, the path conveys a bijective image between the fibers via and through the lifting property .
Universal overlay
An overlay is called a universal overlay if it is simply connected.
As a rule, there are many different overlays over a topological space . For example, superimposing and superimposing , so is a superposition of . The name " universal overlay" comes from the fact that it is also an overlay of any other related overlay of .
From the described universal property it follows that the universal overlay is uniquely determined up to one homeomorphism (namely, because of this property, two universal overlays are each the overlay of the other, from which it follows that they must be homeomorphic).
Is connected , locally connected by path and semilocal simply connected , then has a universal superposition. The universal superposition can be constructed by fixing a point in and looking at each point in the set of homotopy classes of paths from to . The topology is obtained locally because it has an environment whose loops can be contracted globally and on which the said homotopy classes must therefore be the same everywhere, so that the cross product of the environment with the (discretely topologized) set of homotopy classes can be provided with the product topology. Under the conditions mentioned, this construct is then a universal overlay.
The universal overlay of is usually referred to with .
The above example is a universal overlay. Another example is the universal superimposition of the projective space by the sphere
for .
The group of deck transformations, regular overlays
A deck transformation of an overlay is a homeomorphism that is compatible with the projection ; H. . The set of all deck transformations of the overlay forms a group with the link of the sequential execution . The deck transformation group ( deck group for short ) is denoted by.
From the compatibility with the projection it follows that each deck transformation maps a point from back to a point in the same fiber. Since the deck transformations are also homeomorphisms, i.e. bijective, the elements of a fiber are permuted . This defines a group operation of the deck transform group on each fiber.
If an overlay map is and (and therefore also ) contiguous and locally path-contiguous, the operation of is free on each fiber . If the operation is transitive on one fiber, it is on all fibers. In this case the overlay is called normal , regular or Galois . This is exactly the case when the characteristic subgroup is a normal subgroup, which explains the name.
For example, every universal overlay is regular. Likewise the example . Here the deck transformations consist of multiplications with -th roots of unity, so the group is isomorphic to the cyclic group of the order .
The group of the deck transformations of the universal superposition is isomorphic to the fundamental group of the base space; the universal overlay of is a - principal bundle .
classification
have a universal overlay and be a point of . The following two constructions provide an equivalence of categories between the category of superpositions of and the category of sets with -operation:
- The fiber is assigned to an overlay .
- An amount , the associated bundle assigned; it is a fiber bundle with discrete fibers, i.e. an overlay.
Related overlays correspond to sets with a transitive -operation, and apart from isomorphism these are classified by subsets of. The subgroup corresponds to a coherent overlay .
literature
- Edwin H. Spanier: Algebraic Topology. 1. corrected Springer edition, reprint. Springer, Berlin et al. 1995, ISBN 3-540-90646-0 .
Web links
- Coverings of the Circle (computer animation overlays)

![X = [0.1] \ times S ^ {1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ecfebcfe87fcb8d16f87d9f6dfecca71bf16af1)
















































