Composition (mathematics)

The composition of functions

The term composition in the mean mathematics usually the series connection of functions , also known as concatenation , link or successive application called. It is usually noted with the help of the concatenation symbol. ${\displaystyle \circ }$

The representation of a function as a concatenation of two or more, generally simpler functions is important, for example in differential and integral calculus, when it comes to calculating derivatives with the chain rule or integrals with the substitution rule .

The term composition can be generalized from functions to relations and partial functions .

definition

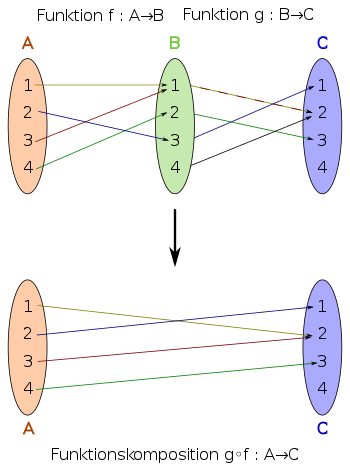
Let be arbitrary sets and as well as functions, then the function is called ${\displaystyle A,B,C}$ ${\displaystyle f\colon \,A\to B}$ ${\displaystyle g\colon \,B\to C}$

${\displaystyle g\circ f\colon \,A\to C,\,x\mapsto (g\circ f)(x):=g(f(x)),}$

the composition of and . The expression “ ” is read as “ linked with ”, “ composed with ”, “ after ” or “ kringel ”. It should be noted that the figure applied first is on the right, in contrast to the diagram, where it is on the left: ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle g\circ f}$ ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle f}$

${\displaystyle A\,\,{\stackrel {f}{\to }}\,\,B\,\,{\stackrel {g}{\to }}\,\,C.}$

Different spellings

An alternative notation for is , whereby one must not confuse this with the product of the functions , in which the multiplication sign is also often omitted. ${\displaystyle g\circ f}$ ${\displaystyle gf}$ ${\displaystyle g\cdot f}$

There are also few authors who write after as with , i.e. evaluate the functions from left to right. Which order was chosen can often be understood from an example given by the author. There is also the notation in which the function symbol is written to the right of the argument, i.e. (or also ) instead of . Then the evaluation from left to right is obvious, i.e. (mainly common in the context of (right) group operations ). ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle f\circ g}$ ${\displaystyle x\mapsto (f\circ g)(x):=g(f(x))}$ ${\displaystyle xf}$ ${\displaystyle x^{f}}$ ${\displaystyle f(x)}$ ${\displaystyle x^{fg}=(x^{f})^{g}}$

Examples

Consider the following functions, for which the set of real numbers or a subset of them is assumed as the set of definitions and values . If the function is given by and the function is given by, the concatenation of and results in the function with ${\displaystyle \mathbb {R} }$ ${\displaystyle g}$ ${\displaystyle g(x)=x^{2}}$ ${\displaystyle f}$ ${\displaystyle f(x)=x+1}$ ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle h}$

${\displaystyle h(x)=\left(g\circ f\right)(x)=\left(x+1\right)^{2}}$.

Conversely, the function defined by can be represented as, where ${\displaystyle h(x)=1/(x^{2}+1)}$ ${\displaystyle h=g\circ f}$

${\displaystyle f(x)=x^{2}+1}$

${\displaystyle g(x)={\frac {1}{x}}~~(x\neq 0)}$

are.

properties

Associativity

The composition of functions is associative , i.e. for functions , and applies: ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle h}$

${\displaystyle \left(h\circ g\right)\circ f=h\circ \left(g\circ f\right)}$ ,

there

${\displaystyle ((h\circ g)\circ f)(x)=(h\circ g)(f(x))=h(g(f(x)))}$

${\displaystyle (h\circ (g\circ f))(x)=h((g\circ f)(x))=h(g(f(x)))}$

for everyone . This associativity only applies to the composition, the curl. Because the evaluation order is formulated in both cases in the third expression (on the far right), it starts with the innermost bracket , on the right with the application of to the operand and proceeds to the left. ${\displaystyle x\in A}$ ${\displaystyle (f(x))}$ ${\displaystyle f}$ ${\displaystyle x}$

Commutativity

The composition of functions is generally not commutative ; For example, the following applies to the functions and : ${\displaystyle f\left(x\right):=x^{2}}$ ${\displaystyle g\left(x\right):=x+1}$

${\displaystyle (f\circ g)(x)=f(x+1)=(x+1)^{2}=x^{2}+2x+1}$

${\displaystyle (g\circ f)(x)=g\left(x^{2}\right)=x^{2}+1}$

Identical images

The identical image behaves neutrally in the composition , so the following applies to a function : ${\displaystyle f\colon A\to B}$

${\displaystyle f\circ \mathrm {id} _{A}=f=\mathrm {id} _{B}\circ f}$,

where and represent the respective identities on the quantities and . ${\displaystyle \mathrm {id} _{A}}$ ${\displaystyle \mathrm {id} _{B}}$ ${\displaystyle A}$ ${\displaystyle B}$

Injectivity, surjectivity, bijectivity

Important properties that a function can have are ${\displaystyle f\colon A\to B}$

• Injectivity (no element in is assumed multiple times), ${\displaystyle B}$
• Surjectivity (every element in is assumed), ${\displaystyle B}$
• Bijectivity (each element in is accepted and none is accepted multiple times). ${\displaystyle B}$

Each of these properties is carried over to the chaining, so the following applies:

• The composition of injective functions is injective.
• The composition of surjective functions is surjective.
• The composition of bijective functions is bijective.

The opposite applies: Is a concatenation ${\displaystyle g\circ f}$

• injective, so is injective. ${\displaystyle f}$
• surjective, so is surjective. ${\displaystyle g}$
• bijective, so is injective and surjective. ${\displaystyle f}$ ${\displaystyle g}$

iteration

If a representation of a set is in itself, then this function can be linked with itself and the function is obtained , which in turn is a function . As is usual with associative operations, the -th iteration of can now be explained inductively for every natural number by: ${\displaystyle f\colon A\to A}$ ${\displaystyle f^{2}=f^{\langle 2\rangle }:=f\circ f}$ ${\displaystyle A\to A}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle f^{n}}$ ${\displaystyle f}$

${\displaystyle f^{1}:=f\ }$

${\displaystyle f^{n+1}:=f\circ f^{n}}$

You also bet

${\displaystyle f^{0}:=\mathrm {id} _{A}\ }$,

with the identical mapping as the neutral element of the chain. ${\displaystyle \mathrm {id} _{A}\ }$

${\displaystyle f^{n}=f^{\langle n\rangle }}$is called the -th iterate (often also the -th power ) of . ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle f}$

If a multiplication is defined, the iteration (of the concatenation) must not be confused with the exponentiation (iteration of the multiplication): in this case it can also denote the expression (see also § Notation ). ${\displaystyle A}$ ${\displaystyle f^{2}(x)}$ ${\displaystyle f(x)\cdot f(x)}$

If bijective, then the inverse function exists and the negative iterations are defined by: ${\displaystyle f}$ ${\displaystyle f^{-1}}$ ${\displaystyle f^{-n}}$

${\displaystyle f^{-n}:={\left(f^{-1}\right)}^{n}\ }$

Examples

Let be the set of positive real numbers and given by . Then: ${\displaystyle A}$ ${\displaystyle f}$ ${\displaystyle f\left(x\right):=x^{2}}$

${\displaystyle f^{3}(x)=x^{8}\ }$

${\displaystyle f^{-2}(x)={\sqrt[{4}]{x}}\ }$

Algebraic structures

Is the amount of all functions of a given amount considered in itself, the composition defines an internal binary operation on , with respect to the (having the identical mapping as a neutral element) a Monoid is. ${\displaystyle {\mathcal {F}}(A)}$ ${\displaystyle A}$ ${\displaystyle {\mathcal {F}}(A)}$ ${\displaystyle {\mathcal {F}}(A)}$

If only bijective functions are used, the monoid is even a group with the respective inverse function as the inverse element . If the set is finite with elements, then we are dealing with the symmetric group . ${\displaystyle A}$ ${\displaystyle n}$ ${\displaystyle S_{n}}$

Structurally compatible images

In mathematics, one often looks at sets with an additional structure, as well as maps that are compatible with this structure, for example

• linear mappings between vector spaces
• continuous mapping between topological spaces
• Group homomorphisms between groups

It is now desirable that the structural compatibility is retained in the composition, and in fact the following applies in the examples:

• The composition of linear images is linear.
• The composition of continuous images is continuous.
• The composition of group homomorphisms is a group homomorphism.

These considerations lead to the category theory , in which one even abstracts from the fact that it is a question of images and only requires associativity and the property of identities for the composition.

Composition of relations

To a function which is function graph a relation . With regard to the composition of functions, the following applies (using the infix notation ): ${\displaystyle f\colon X\rightarrow Y}$ ${\displaystyle \{(x,f(x))\mid x\in X\}}$ ${\displaystyle R_{f}\subseteq X\times Y}$

${\displaystyle x\ R_{g\circ f}\ z\Leftrightarrow \exists y:x\ R_{f}\ y\ R_{g}\ z}$.

This observation leads to the definition of the composition of two-digit relations and : The relation is given by ${\displaystyle R\subseteq X\times Y}$ ${\displaystyle S\subseteq Y\times Z}$ ${\displaystyle S\circ R\subseteq X\times Z}$

${\displaystyle x\ S\circ R\ z:\Leftrightarrow \exists y:x\ R\ y\ S\ z}$.

When composing relations, the order from right to left is always followed.

example

${\displaystyle X}$be the set of points , the set of lines and the set of planes in three-dimensional space. The relations and are determined by: ${\displaystyle Y}$ ${\displaystyle Z}$ ${\displaystyle R}$ ${\displaystyle S}$

${\displaystyle x~R~y\Leftrightarrow }$the point lies on the straight line ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle y~S~z\Leftrightarrow }$the line is in the plane included ${\displaystyle y}$ ${\displaystyle z}$

The following applies to the composition : ${\displaystyle T:=S\circ R}$

${\displaystyle x~T~z\Leftrightarrow }$the point lies in the plane ${\displaystyle x}$ ${\displaystyle z}$

properties

• The composition of relations is associative.
• Denotes the identical relation on a set , i.e. the set of all pairs , then for every relation : ${\displaystyle \mathrm {id} _{M}}$ ${\displaystyle M}$ ${\displaystyle \left(m,m\right)\in M^{2}}$ ${\displaystyle R\subseteq X\times Y}$

  ${\displaystyle \mathrm {id} _{Y}\circ R=R=R\circ \mathrm {id} _{X}}$

• If a relation is on a set , then all powers are also (with ) defined. These powers are used, for example, in the definition of the reflexive-transitive envelope . A relation with is called transitive . ${\displaystyle R\subseteq X^{2}}$ ${\displaystyle X}$ ${\displaystyle R^{n}}$ ${\displaystyle n\geq 0}$ ${\displaystyle R}$ ${\displaystyle R\circ R\subseteq R}$

Different notation in physics

In physics and other natural sciences, it is common to identify the concatenation of a function with the "external function" . Because of this notation, equations sometimes arise in physical literature that at first glance are incorrect or meaningless according to current mathematical conventions, for example ${\displaystyle f=f\circ g}$

${\displaystyle V({\vec {x}})=V(|{\vec {x}}|)}$,

where is the position vector of the point and its Euclidean longitude . From a mathematical point of view, this equation is in principle wrong, since on the left side of the equation represents a function (you should insert it into an element ), on the right side it evidently shows a subset of the real numbers as the domain of definition, i.e. , since you use the scalar quantity sets in. What is meant by this intuitive equation, however, is that (for a special case considered) the physical quantity (in this case a potential ), which is generally a function of the location, can be described with a function that only depends on the distance between the location and the zero point depends. A mathematically "clean" formulation of this statement would be something like: ${\displaystyle {\vec {x}}=(x_{1},x_{2},x_{3})}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle |{\vec {x}}|={\sqrt {x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}}}$ ${\displaystyle V}$ ${\displaystyle D\subset \mathbb {R} ^{3}\rightarrow \mathbb {R} }$ ${\displaystyle V}$ ${\displaystyle {\vec {x}}\in \mathbb {R} ^{3}}$ ${\displaystyle V}$ ${\displaystyle V\colon I\subset \mathbb {R} \rightarrow \mathbb {R} }$ ${\displaystyle V}$ ${\displaystyle |{\vec {x}}|}$ ${\displaystyle V}$ ${\displaystyle {\vec {x}}}$

${\displaystyle \exists {\bar {V}}\colon I\subset \mathbb {R} \rightarrow \mathbb {R} :V({\vec {x}})={\bar {V}}(|{\vec {x}}|)}$

${\displaystyle V}$is therefore a concatenation of the scalar function and the Euclidean norm : ${\displaystyle {\bar {V}}}$ ${\displaystyle d\colon \mathbb {R} ^{3}\rightarrow \mathbb {R} ,d({\vec {x}})=|{\vec {x}}|}$

${\displaystyle V={\bar {V}}\circ d}$.

We obtain the above, intuitive notation of this equation by first identifying the link symbolically with the external function and this in turn with the potential . The advantages of notation are intuitively understandable spellings and a small number of different symbols. A typical example of a function that satisfies the above equation is the central potentials of the form ${\displaystyle {\bar {V}}\circ d}$ ${\displaystyle {\bar {V}}}$ ${\displaystyle V}$ ${\displaystyle V\colon \mathbb {R} ^{3}\backslash \{0\}\rightarrow \mathbb {R} }$

${\displaystyle V({\vec {x}})={\frac {\alpha }{|{\vec {x}}|}},}$

the u. a. used in electrostatics . is in this case a concatenation of the scalar function with ${\displaystyle V}$ ${\displaystyle {\bar {V}}\colon \mathbb {R} \backslash \{0\}\rightarrow \mathbb {R} }$

${\displaystyle {\bar {V}}(x)={\frac {\alpha }{x}}}$

with the Euclidean norm:

${\displaystyle V({\vec {x}})={\bar {V}}(|{\vec {x}}|)}$

literature

• Composition . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).

Individual evidence

1. ↑ Gerd Fischer: Linear Algebra . Springer, 2009, p. 36 .
2. ↑ Ehrhard Behrends: Analysis Volume 1 . Springer, 2014, p. 19 .
3. ↑ George Hoever: Higher Mathematics compact . Springer, 2013, p. 43 .

Web links

Wikibooks: Math for non-freaks: Figure: Functional  composition - learning and teaching materials